河北省保定市易县2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-07-28 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点 $P (- 2 ， - 3)$ 所在的象限是 $($ 　　 $)$

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列各数中是无理数的是（）．

A、 $3.1415926$ B、0 C、 $\sqrt{3}$ D、4

查看试题解析
3. 下列选项中， $∠ 1$ 和 $∠ 2$ 是对顶角的是（）

A、 B、 C、 D、

查看试题解析
4. 用代入法解方程组 ${\begin{array}{l} 2 x - y = 5 ， \\ y = 1 + x \end{array}$ 时，代入正确的是（）

A、 $2 x - 1 + x = 5$ B、 $x - 1 + x = 5$ C、 $x - 1 - x = 5$ D、 $2 x - 1 - x = 5$

查看试题解析
5. 要了解某校 $1000$ 名初中生的课外负担情况，若采用抽样调查的方法进行调查，则下列样本选择最具有代表性的是（）

A、调查全体女生 B、调查全体男生 C、调查九年级全体学生 D、调查七、八、九年级各 $100$ 名学生

查看试题解析
6. 把一根 $14 c m$ 的木棒截成 $2 c m$ 和 $3 c m$ 两种规格的小木棒，在不浪费材料的情况下，截法有（）

A、1种 B、2种 C、3种 D、4种

查看试题解析
7. 如图，直线 $l_{1} ∥ l_{2}$ ，将三角板按如图方式放置，直角顶点在 $l_{2}$ 上．若 $∠ 1 = 36 °$ ，则 $∠ 2 =$ （）

A、36° B、45° C、54° D、64°

查看试题解析
8. 如图所示，从A到B有 $① ② ③$ 三条路可以走，每条路长分别为L，M，N，则L，M，N的大小关系是 $()$ ．

A、 $L > M > N$ B、 $L = M > N$ C、 $M > N > L$ D、 $L > N > M$

查看试题解析
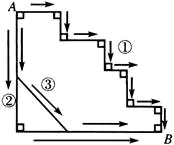9. 疫情期间进行线上教学，为保证学生的身体健康，某校规定四项特色活动：舞蹈、跳绳、踢毽、武术，要求每位学生任选一项在家锻炼，小明从全校1200名学生中随机调查了部分学生，对他们所选活动进行了统计，并绘制了尚不完整的条形图和扇形图，如图所示，下列结论错误的是（）

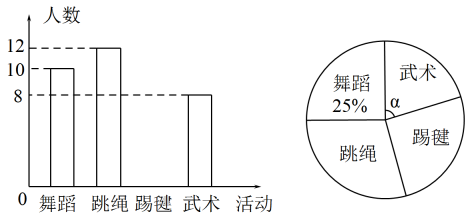A、调查了40名学生 B、被调查的学生中，选踢毽的有10人 C、 $α = 72 °$ D、全校选舞蹈的估计有250人

查看试题解析
10. 如图，在下列条件中，能判断 $A B ∥ C D$ 的是（）

A、 $∠ B A D + ∠ A D C = 180 °$ B、 $∠ B A D = ∠ B C D$ C、 $∠ 1 = ∠ 2$ D、 $∠ 3 = ∠ 4$

查看试题解析
11. 若正方体的体积为9，则棱长a的取值范围是（）

A、3 B、 $1.5 < a < 2$ C、 $2 < a < 2.5$ D、 $2.5 < a < 3$

查看试题解析
12. 某班45名学生的成绩被分为5组，第1～4组的频数分别为12，11，9，4，则第5组的频率是（）

A、0.1 B、0.2 C、0.3 D、0.4

查看试题解析
13. 关于 $x$ 的一元一次不等式组 ${\begin{array}{l} x + 6 \leq 8 \\ x - 7 < 2 (x - 3) \end{array}$ 的解集为（）

A、 $x \leq 2$ B、 $x < 1$ C、 $1 < x \leq 2$ D、 $- 1 < x \leq 2$

查看试题解析
14. 如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30°，那么这两个角是（）

A、42°、138° B、都是10° C、42°、138°或10°、10° D、以上都不对

查看试题解析
15. 已知关于 $x ， y$ 的二元一次方程组 ${\begin{array}{l} a_{1} x + b_{1} y = 21 \\ a_{2} x + b_{2} y = 12 \end{array}$ 的解是 ${\begin{array}{l} x = 3 \\ y = 6 \end{array}$ ，则关于 $m$ 和 $n$ 的方程组 ${\begin{array}{l} a_{1} (2 m + n) + b_{1} (m - n) = 21 \\ a_{2} (2 m + n) + b_{2} (m - n) = 12 \end{array}$ 的解是（）

A、 ${\begin{array}{l} m = 3 \\ n = 6 \end{array}$ B、 ${\begin{array}{l} m = 3 \\ n = - 3 \end{array}$ C、 ${\begin{array}{l} m = 2 \\ n = 3 \end{array}$ D、 ${\begin{array}{l} m = 2 \\ n = - 3 \end{array}$

查看试题解析
16. 如图， $A B = 6$ ，点A到直线 $B C$ 的距离为3，若在射线 $B C$ 上只存在一个点 $P$ ，记 $A P$ 的长度为 $d$ ，则 $d$ 的值可以是（）

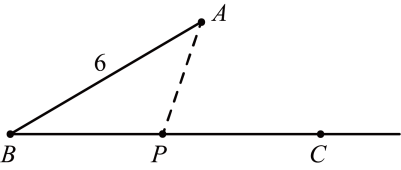A、7 B、2 C、5 D、6

查看试题解析

二、填空题

17. 如果某个数的一个平方根是 $- 5$ ，那么这个数的算术平方根是．

查看试题解析
18. 已知点 $P (a + 1 ， 2 a - 3)$ ， $Q (2 ， 3)$ ，当点 $P$ 在第一、三象限的角平分线上时，点 $P$ 的坐标为；当 $P Q ∥ x$ 轴时， $P Q =$ ．

查看试题解析
19. 如图，在平面直角坐标系中，对正方形 $A B C D$ 及其内部的每个点进行如下操作：把每个点的横、纵坐标都乘以同一个实数a，将得到的点先向右平移m个单位长度，再向上平移n个单位长度 $(m > 0 ， n > 0)$ ，得到正方形 $A^{'} B^{'} C^{'} D^{'}$ 及其内部的点，其中点A，B的对应点分别为 $A^{'}$ ， $B^{'}$ ．已知正方形 $A B C D$ 内部的一点F经过上述操作后得到的对应点 $F^{'}$ 与点F重合．

(1)、 $m =$ ， $n =$ ．

(2)、点F的坐标是．

查看试题解析

三、解答题

20.

(1)、计算： $\sqrt{9} - \sqrt[3]{8} + \sqrt{0.01}$ ；

(2)、解方程组： ${\begin{array}{l} 2 x - 3 y = 7 ① \\ x + 2 y = 0 ② \end{array}$ ．

查看试题解析
21. 某校七年级1班体育委员统计了全班同学60秒跳绳的次数，并绘制出如下频数分布表和频数分布直方图：
次数
          $80 \leq x < 100$
          $100 \leq x < 120$
          $120 ≤ x < 140$
          $140 ≤ x < 160$
          $160 ≤ x < 180$
          $180 \leq x < 200$
频数
a
4
12
15
8
3
结合图表解答下列问题：

(1)、 $a =$ ，全班人数是．

(2)、补全频数分布直方图．

(3)、若跳绳次数不少于160的学生成绩为优秀，则优秀学生人数占全班总人数的百分之几？

查看试题解析
22. 如图，在平面直角坐标内有三角形 $A B C$ ，其中 $A (1 ， 3)$ ， $B (- 3 ， 1)$ ， $C (- 1 ， 0)$ ，在坐标平面内放置一透明胶片，并在胶片上描画出点A．平移该胶片使点A落在点 $A^{'} (5 ， 3)$ 处．

(1)、若点B，点C都与点A做同样的平移运动，点B，C平移后的对应点分别为点 $B^{'}$ ， $C^{'}$ ，写出点 $B^{'}$ ， $C^{'}$ 的坐标， $B^{'}$ ▲ ， $C^{'}$ ▲ ，并在坐标平面内画出三角形 $A^{'} B^{'} C^{'}$ ．

(2)、求三角形 $A^{'} B^{'} C^{'}$ 的面积．

查看试题解析
23. 已知：如图，EF∥CD，∠1+∠2=180°

(1)、判断GD与CA的位置关系，并说明理由；

(2)、若CD平分∠ACB，DG平分∠CDB，且∠A=40°，求∠ACB的度数。

查看试题解析
24. 如图，在一条不完整的数轴上从左到右有点A，B，C，其中 $A B = 2$ ， $B C = 1$ ．设点A，B，C在数轴上所对应数的和是P．

(1)、若P的值不大于11，求点A表示的数x的最大值．

(2)、若原点O在图中数轴上点C的右边a个单位长度，且P不小于 $- 22$ ，求a的最大值．

查看试题解析

25. 某公司装修需用A型板材240块、B型板材180块，A型板材规格是

a c m \times 30 c m

， B型板材规格是

b c m \times 30 c m

．现只能购得规格是

150 c m \times 30 c m

的标准板材．一张标准板材尽可能多地裁出A型、B型板材，共有下列三种裁法：（图1是裁法一的裁剪示意图）

	裁法一	裁法二	裁法三
A型板材块数	1	2	0
B型板材块数	2	m	n

若每张标准板材裁出1个A型板材，2个B型板材，则剩余 $10 c m$ ；若每张标准板材裁出2个A型板材，剩余的材料还差 $10 c m$ 才能再裁出一个B型板材．

(1)、求a，b的值．

(2)、

m =

，

n =

．

(3)、设所购的标准板材全部裁完，其中按裁法一裁了x张、按裁法二裁了y张、按裁法三裁了z张，且所裁出的A，B两种型号的板材刚好够用．若按照裁法一裁的张数不少于60张，求x的取值范围．

查看试题解析

26. 如图，在平面直角坐标系中， $A D ∥ B C$ ， $D C ∥ A B$ ， $A (- 1 ， 0)$ ， $B (0 ， \sqrt{5})$ ， $D (3 ， 0)$ ， $∠ A = 60 °$ ，点P在射线 $A D$ 上运动，连接 $P B$ ，沿 $P B$ 将三角形 $A P B$ 折叠，得到三角形 $A^{'} P B$ ．

(1)、当点P在线段 $A D$ 上， $∠ D P A^{'} = 20 °$ 时， $∠ A P B =$ ．

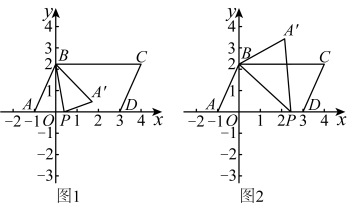(2)、①在图1，图2两种情况下，分别求 $∠ B A^{'} P$ ， $∠ C B A^{'}$ 与 $∠ D P A^{'}$ 之间的数量关系．
②除了①中两种情况以外，还有其他情况吗？如果有，请直接写出这三个角的数量关系．

查看试题解析

次数	$80 \leq x < 100$	$100 \leq x < 120$	$120 ≤ x < 140$	$140 ≤ x < 160$	$160 ≤ x < 180$	$180 \leq x < 200$
频数	a	4	12	15	8	3