河北省承德市丰宁县2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-07-28 类型：期末考试

进入出卷网下载

一、单选题

1. 代数式 $- 2 x$ 的意义可以是（）

A、 $- 2$ 与 $x$ 的和 B、 $- 2$ 与 $x$ 的差 C、 $- 2$ 与 $x$ 的积 D、 $- 2$ 与 $x$ 的商

查看试题解析
2. 如图，在平面直角坐标系 $x O y$ 中，★位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 如图，某人沿路线 $A \to B \to C \to D$ 行走， $A B$ 与 $C D$ 方向相同， $∠ 1 = 128 °$ ，则 $∠ 2 =$ （）

A、 $52 °$ B、 $118 °$ C、 $128 °$ D、 $138 °$

查看试题解析
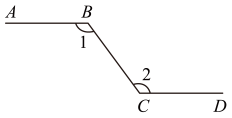4. 光年是天文学上的一种距离单位，一光年是指光在一年内走过的路程，约等于 $9.46 \times 1 0^{12} k m$ ．据探测某星体距离地球约为2光年，则2光年用科学记数法表示为（）

A、 $9.46 \times 1 0^{13}$ B、 $18.92 \times 1 0^{12}$ C、 $1.892 \times 1 0^{13}$ D、 $1.892 \times 1 0^{14}$

查看试题解析
5. 如图，将 $△ A B C$ 沿 $B C$ 向右平移得到 $△ D E F$ ，若 $B C = 5$ ， $E C = 3$ ，则 $C F$ 的长是（）

A、2 B、2.5 C、3 D、5

查看试题解析
6. 已知 ${\begin{array}{l} x = - 3 \\ y = 2 \end{array}$ 是方程 $2 x + k y = 6$ 的解，则 $k$ 等于（）

A、3 B、4 C、5 D、6

查看试题解析
7. 估计面积为6的正方形的边长大小，应该在下面的整数（）

A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间

查看试题解析
8. 下列算式的计算结果不为0的是（）

A、 $- 2 + \sqrt{{(- 2)}^{2}}$ B、 $- 2 + \sqrt[3]{- 8}$ C、 $- 2 + {(- \sqrt{2})}^{2}$ D、 ${(\sqrt{2})}^{2} - \sqrt{2^{2}}$

查看试题解析
9. 不等式组 ${\begin{array}{l} 2 x > x - 1 \\ x + 1 \leq 3 \end{array}$ 的整数解有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 下列图形中，是长方体表面展开图的是（）

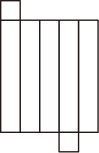A、 B、 C、 D、

查看试题解析
11. 若 $2 m - 4$ 与 $3 m - 1$ 是同一个正数的两个平方根，则这个正数为（）

A、1 B、4 C、 $± 1$ D、 $\pm 4$

查看试题解析
12. 为调查某校学生对“2023年全国两会”的了解程度，某课外活动小组进行了抽样调查，下列样本中最具有代表性的是（）

A、调查该校九年级的学生对“2023年全国两会”的了解程度 B、调查该校女生对“2023年全国两会”的了解程度 C、调查该校在篮球场打篮球的学生对“2023年全国两会”的了解程度 D、调查该校每班学号尾号为5的学生对“2023年全国两会”的了解程度

查看试题解析
13. 如果点 $A (m ， n)$ 在平面直角坐标系中的第四象限内，则下列不等式中正确的是（）

A、 $m n > 0$ B、 $m < n^{3}$ C、 $m - n > 0$ D、 $m + n^{2} < 0$

查看试题解析
14. $m$ 加3的和与 $- m + 1$ 的差小于13，则 $m$ 的值不可能为（）

A、6 B、5 C、4 D、3

查看试题解析
15. 《孙子算经》记载：“今有木，不知长短．引绳度之，余绳四尺五寸；屈绳量之，不足一尺．木长几何？”（尺、寸是长度单位，1尺＝10寸）．意思是，现有一根长木，不知道其长短．用一根绳子去度量长木，绳子还剩余4.5尺；将绳子对折再度量长木，长木还剩余1尺．问长木长多少？设长木长为x尺，则可列方程为（）

A、 $\frac{1}{2} (x + 4.5) = x - 1$ B、 $\frac{1}{2} (x + 4.5) = x + 1$ C、 $\frac{1}{2} (x - 4.5) = x + 1$ D、 $\frac{1}{2} (x - 4.5) = x - 1$

查看试题解析
16. 用圆圈按如图所示的规律拼图案，其中第①个图案中有2个圆圈，第②个图案中有5个圆圈，第③个图案中有8个圆圈，第④个图案中有11个圆圈，…，按此规律排列下去，则第⑦个图案中圆圈的个数为（）

A、14 B、20 C、23 D、26

查看试题解析

二、填空题

17. 请写出一个正整数 $m$ 的值使得 $\sqrt{8 m}$ 也是整数，则 $m$ 的最小值是．

查看试题解析
18. 已知 $| a - 1 | + \sqrt{8 - b} = 0$ ，则 $\sqrt{a + b} =$ ．

查看试题解析
19. 如图，货船A与港口B相距30海里，我们用有序数对（南偏西 $40 °$ ， 30海里）来描述港口B相对货船A的位置，那么货船A相对港口B的位置可描述为．

查看试题解析
20. 已知：某小区地下停车场的栏杆如图所示，当栏杆抬起到最大高度时∠ABC=150°，若此时CD平行地面AE，则 $∠ B C D =$ 度．

查看试题解析

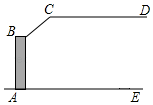
三、解答题

21.

(1)、计算： $\sqrt[3]{- 8} + | 2 - \sqrt{5} | + \sqrt{{(- 3)}^{2}}$ ．

(2)、解方程组： ${\begin{array}{l} 2 x + y = 3 ① \\ 4 x - 3 y = 1 ② \end{array}$ ．

查看试题解析
22. 如图，已知点A表示数 $- 3$ ，点B表示数1．若 $| m | = 2$ ，在数轴上表示数m的点位于点A，B之间，表示数n的点在点A右侧且与点B的距离为5．

(1)、 $m =$ ； $n =$ ； $m + n - m n =$ ；

(2)、解关于 $x$ 的不等式组 ${\begin{array}{l} m x + 2 < n \\ n x - 4 \leq - 4 m \end{array}$ ，并把解集表示在图所示的数轴上．

查看试题解析
23. 在校园艺术节活动中，同学们踊跃参加各项竞赛活动，参加的学生只能从“歌曲”，“舞蹈”，“小品”，“主持”和“乐器”五个选项中选择一项．现将选择情况绘制成了条形统计图和不完整的扇形统计图，其中条形统计图部分被不小心污染．请根据统计图中的相关信息，回答下列问题：

(1)、图1中，根据数据信息可知：参加“主持”比赛的人数是参加“乐器”比赛人数的倍，而统计图表现出来的直观情况却是：参加“主持”比赛的人数是参加“乐器”比赛人数的3倍，两个结果之所以不一样，是因为；

(2)、请求出全校一共有多少名学生参加“舞蹈”比赛？

(3)、在图2中，“小品”部分所对应的圆心角的度数为度；

(4)、拟参加比赛活动的学生有 $50 %$ 获奖，其中获二等奖与三等奖的人数之比 $3 ： 5$ ，二等奖人数是一等奖人数的1.5倍，直接写出获一等奖的学生有人．

查看试题解析
24. 创建文明城市，构建美好家园．为提高垃圾分类意识，幸福社区决定采购A，B两种型号的新型垃圾桶．若购买3个A型垃圾桶和4个B型垃圾桶共需要580元，购买6个A型垃圾桶和5个B型垃圾桶共需要860元．

(1)、求两种型号垃圾桶的单价；

(2)、若需购买A，B两种型号的垃圾桶共200个，总费用不超过15000元，至少需购买A型垃圾桶多少个？

查看试题解析
25. 已知：如图，在平面直角坐标系中，三角形 $A B C$ 的三个顶点坐标分别是 $A (1 ， 0)$ ， $B (- 2 ， 3)$ ， $C (- 3 ， 0)$ ．

(1)、线段 $A C$ 的中点的坐标，三角形 $A B C$ 的面积是；

(2)、若点 $A$ 、 $C$ 的位置不变，当点 $P$ 在 $y$ 轴上时，且三角形 $A C P$ 的面积等于三角形 $A B C$ 的面积的2倍，则 $P$ 的坐标是；

(3)、若点 $B$ 、 $C$ 的位置不变，当点 $Q$ 在 $x$ 轴上时，且三角形 $B C Q$ 的面积等于三角形 $A B C$ 的面积的2倍，求点 $Q$ 的坐标；

(4)、若点 $M (m ， 0)$ 是三角形 $A B C$ 的 $A C$ 边上的一点，直接写出三角形 $A B C$ 向右平移3个单位，向下平移2个单位后，点 $M$ 的对应点 $M_{1}$ 的坐标（用含 $m$ 的代数式表示）．

查看试题解析
26. 问题情境：在数学探究活动课上，老师让同学们以“两条平行线 $A B$ ， $C D$ 和一块含30°角的直角三角板 $A_{1} B_{1} C_{1} (∠ C_{1} = 90 ° ， ∠ A_{1} = 30 °)$ ”为主题开展数学探究活动．

(1)、探究发现：如图-1，小明把三角板 $A_{1} B_{1} C_{1}$ 的60°角的顶点 $B_{1}$ 放在 $C D$ 上，若 $∠ 1 = 2 ∠ 2$ ，则 $∠ 2 =$ °；

(2)、如图-2，小亮把三角板 $A_{1} B_{1} C_{1}$ 的两个锐角的顶点 $A_{1}$ ， $B_{1}$ 分别放在 $A B$ 和 $C D$ 上，请你探索并说明 $∠ A A_{1} C_{1}$ 与 $∠ C_{1} B_{1} C$ 之间的数量关系；

(3)、如图-3，小颖把三角板 $A_{1} B_{1} C_{1}$ 的直角顶点 $C_{1}$ 放在 $C D$ 上，30°角的顶点 $A_{1}$ 放在 $A B$ 上．若 $∠ A A_{1} B_{1} = α$ ，直接写出 $∠ B_{1} C_{1} C$ 的度数（用含 $α$ 的代数式表示）；

(4)、拓展延伸：若将如图-3所示的三角形 $A_{1} B_{1} C_{1}$ 绕直角顶点 $C_{1}$ 顺时针旋转一周，每秒转动10°，直接写出当 $C_{1} B_{1} ⊥ C D$ 时，三角形 $A_{1} B_{1} C_{1}$ 旋转所用的时间 $t$ （用含 $α$ 的代数式表示）．

查看试题解析