河北省承德市平泉市2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-07-28 类型:期末考试
一、单选题
-
1. 表示的意义是( )A、3的立方根 B、3的平方根 C、3的算术平方根 D、3的平方2. 如图,直线与交于点 , 于 , 与的关系是( )
 A、对顶角 B、互余 C、互补 D、相等3. 如图,小手盖住的点的坐标可能是( )
A、对顶角 B、互余 C、互补 D、相等3. 如图,小手盖住的点的坐标可能是( )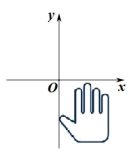 A、 B、 C、 D、4. 下列图形中,由∠1=∠2能得到AB∥CD的是( )A、
A、 B、 C、 D、4. 下列图形中,由∠1=∠2能得到AB∥CD的是( )A、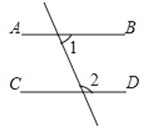 B、
B、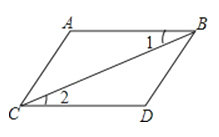 C、
C、 D、
D、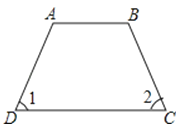 5. 设 , 下列式子不能用“”连接的是( )A、 B、 C、 D、6. 已知方程组的解为 , 则分别为( )A、2,1 B、1,5 C、 , D、1,27. 为了加强学生垃圾分类意识,提高学生垃圾分类能力,某校从全校2000名学生的垃圾分类知识测试卷中随机抽取了200份试卷进行成绩统计,在这个问题中以下说法正确的是( )A、200份试卷的成绩是样本 B、每名学生是个体 C、此调查为全面调查 D、样本容量是20008. 对于下列的叙述,其中不正确的是( )A、两直线平行,同旁内角互补 B、同位角相等,两直线平行 C、过一点有且只有一条直线与已知直线平行 D、两点之间的所有连线中,线段最短9. 如图,天平右盘中的每个砝码的质量都是1克,则物体A的质量m克的取值范围表示在数轴上为( )
5. 设 , 下列式子不能用“”连接的是( )A、 B、 C、 D、6. 已知方程组的解为 , 则分别为( )A、2,1 B、1,5 C、 , D、1,27. 为了加强学生垃圾分类意识,提高学生垃圾分类能力,某校从全校2000名学生的垃圾分类知识测试卷中随机抽取了200份试卷进行成绩统计,在这个问题中以下说法正确的是( )A、200份试卷的成绩是样本 B、每名学生是个体 C、此调查为全面调查 D、样本容量是20008. 对于下列的叙述,其中不正确的是( )A、两直线平行,同旁内角互补 B、同位角相等,两直线平行 C、过一点有且只有一条直线与已知直线平行 D、两点之间的所有连线中,线段最短9. 如图,天平右盘中的每个砝码的质量都是1克,则物体A的质量m克的取值范围表示在数轴上为( ) A、
A、 B、
B、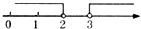 C、
C、 D、
D、 10. , 则值不能为( )A、10 B、8 C、7 D、611. 如图,把两个边长均为1的小正方形分别沿对角线剪开,将四个直角三角形拼成一个大的正方形,则这个大正方形的边长为( )
10. , 则值不能为( )A、10 B、8 C、7 D、611. 如图,把两个边长均为1的小正方形分别沿对角线剪开,将四个直角三角形拼成一个大的正方形,则这个大正方形的边长为( ) A、1 B、1.5 C、 D、12. 琪琪为了研究图1中“跑到画板外面去的两直线所成的角(锐角)”问题,设计出一个方案如图2:则直线所成的角的度数为( )
A、1 B、1.5 C、 D、12. 琪琪为了研究图1中“跑到画板外面去的两直线所成的角(锐角)”问题,设计出一个方案如图2:则直线所成的角的度数为( ) A、 B、 C、 D、13. 如图,嘉嘉和琪琪用不同的方法解方程组 , 两人求x的过程正确的是( )
A、 B、 C、 D、13. 如图,嘉嘉和琪琪用不同的方法解方程组 , 两人求x的过程正确的是( ) A、两人都正确 B、嘉嘉不正确,琪琪正确 C、嘉嘉正确,琪琪不正确 D、两人都不正确14. 如图,的坐标为若将线段平移至为中点,平移后的对应点坐标为( )
A、两人都正确 B、嘉嘉不正确,琪琪正确 C、嘉嘉正确,琪琪不正确 D、两人都不正确14. 如图,的坐标为若将线段平移至为中点,平移后的对应点坐标为( ) A、 B、 C、 D、15. 如果 , , 那么约等于( )A、28.72 B、0.2872 C、13.33 D、0.133316. 已知关于的不等式组 , 下列四个结论:
A、 B、 C、 D、15. 如果 , , 那么约等于( )A、28.72 B、0.2872 C、13.33 D、0.133316. 已知关于的不等式组 , 下列四个结论:①若它的解集是 , 则;②当 , 不等式组有解;③若它的整数解仅有3个,则的取值范围是;④若它无解,则 . 其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
17. 计算:18. 已知 , ①用含的代数式表示 , 则;②当时,;③当时,则的取值范围为: .19. 如图直线在上,为上动点,过作的角平分线交与 , 若 .
 (1)、时, .(2)、 , ;(3)、写出数量关系: .
(1)、时, .(2)、 , ;(3)、写出数量关系: .三、解答题
-
20.(1)、已知两个数和(为负整数),设整式的值为

①当时,求的值;
②若的取值范围如图所示,求的负整数值.
(2)、解不等式组:请结合题意填空,完成本题的解答:
解不等式①,得 ▲ ;
解不等式②,得 ▲ ;
并把不等式①,②解集在数轴上表示出来;
原不等式组的解集为 ▲ .
 21. 数学活动课上,小云和小辉在讨论老师出示的一道二元一次方程组的问题:
21. 数学活动课上,小云和小辉在讨论老师出示的一道二元一次方程组的问题:已知关于的二元一次方程组的解满足③,求的值.

请结合他们的对话,解答下列问题:
(1)、按照小云的方法,x的值为 , y的值为 .(2)、老师说小辉的方法体现了整体代入的思想,请按照小辉的思路求出m的值.22. 为落实国家“双减”政策,某校为学生开展了课后服务,其中在体育类活动中开设了四种运动项目:A跳绳,B排球,C乒乓球,D篮球.为了解学生最喜欢哪一种运动项目,随机抽取部分学生进行调查(每位学生仅选一种),并将调查结果制成如图所示的尚不完整的统计图表.问卷情况统计表
运动项目
人数
A跳绳
B排球
5
C乒乓球
40
D篮球
35
问卷情况扇形统计图
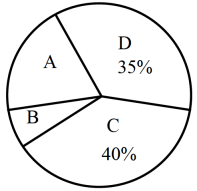 (1)、本次调查的样本容量是 , 统计表中;(2)、在扇形统计图中,“排球”对应的圆心角的度数是;(3)、若该校共有1200名学生,请你估计最喜欢“A跳绳”的学生人数是多少?23. 已知点
(1)、本次调查的样本容量是 , 统计表中;(2)、在扇形统计图中,“排球”对应的圆心角的度数是;(3)、若该校共有1200名学生,请你估计最喜欢“A跳绳”的学生人数是多少?23. 已知点 (1)、当点在轴上时,求点坐标及的面积;(2)、当轴时:
(1)、当点在轴上时,求点坐标及的面积;(2)、当轴时:①求两点之间的距离;
②直接比较 ▲ (填“>”或“<”或“=”)
(3)、点不可能在第象限.24. 已知:如图1,AD∥BC,∠ABC=∠ADC,求证:AB∥CD. (1)、请补充下面证明过程
(1)、请补充下面证明过程证明:∵AD∥BC(已知)
∴∠ ▲ +∠ABC =180°( )
∵∠ABC=∠ADC(已知)
∴∠ ▲ +∠ADC =180°( )
∴AB∥CD( )
(2)、某同学想到了另一种证法,请你补充完整他的证明过程.证明:连接BD,如图2.
25. 2023年是癸卯兔年,嘉琪记录了她的妈妈连续两天购买A,B两种兔年饰品账目:(A,B两种兔年饰品单价不变)第一天购买3个A种饰品和2个B种饰品共84元;
第二天购买4个A种饰品和1个B种饰品共32元.
(1)、妈妈说她的记录错误,请帮她说明错误理由.(2)、结果嘉琪发现第一天错把34元写成84元,从而求出每个A种饰品单价6元,每个B种饰品单价8元,妈妈决定再次购买A种饰品和B种饰品共20个,总费用不超过150元,那么最多可以购买多少个A种饰品?26. 探究问题:已知 , 画一个角 , 使 , 且交于点P.与有怎样的数量关系?(1)、我们发现与有两种位置关系:如图1与图2所示.
①图1中与数量关系为 ▲ ;
图2中与数量关系为 ▲ ;
②请根据图1情况完成下面推理过程.
(已知) ▲ ( )
( )
▲ . (等量代换)
③由①得出一个真命题(用文字叙述): ▲ .
(2)、应用③中的真命题,解决以下问题:若两个角的两边互相平行,且一个角比另一个角的3倍少 , 求这两个角的度数.