四川省巴中市2023年中考数学试卷
试卷更新日期:2023-07-28 类型:中考真卷
一、选择题(本大题共12小题,共48.0分。)
-
1. 下列各数为无理数的是( )A、 B、 C、 D、2. 如图所示图形中为圆柱的是( )A、
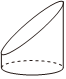 B、
B、 C、
C、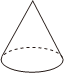 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、多边形的外角和为 B、 C、 D、可能性很小的事情是不可能发生的5. 一次函数的函数值随增大而减小,则的取值范围是( )A、 B、 C、 D、6. 某同学学习了正方体的表面展开图后,在如图所示的正方体的表面展开图上写下了“传承红色文化”六个字,还原成正方体后,“红”的对面是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、多边形的外角和为 B、 C、 D、可能性很小的事情是不可能发生的5. 一次函数的函数值随增大而减小,则的取值范围是( )A、 B、 C、 D、6. 某同学学习了正方体的表面展开图后,在如图所示的正方体的表面展开图上写下了“传承红色文化”六个字,还原成正方体后,“红”的对面是( ) A、传 B、承 C、文 D、化7. 若满足 , 则代数式的值为( )A、 B、 C、 D、8. 如图,是的外接圆,若 , 则( )
A、传 B、承 C、文 D、化7. 若满足 , 则代数式的值为( )A、 B、 C、 D、8. 如图,是的外接圆,若 , 则( ) A、 B、 C、 D、9. 某学校课后兴趣小组在开展手工制作活动中,美术老师要求用张卡纸制作圆柱体包装盒,准备把这些卡纸分成两部分,一部分做侧面,另一部分做底面已知每张卡纸可以裁出个侧面,或者裁出个底面,如果个侧面和个底面可以做成一个包装盒,这些卡纸最多可以做成包装盒的个数为( )A、 B、 C、 D、10. 如图,在中, , , 、分别为、中点,连接、相交于点 , 点在上,且:: , 则四边形的面积为( )
A、 B、 C、 D、9. 某学校课后兴趣小组在开展手工制作活动中,美术老师要求用张卡纸制作圆柱体包装盒,准备把这些卡纸分成两部分,一部分做侧面,另一部分做底面已知每张卡纸可以裁出个侧面,或者裁出个底面,如果个侧面和个底面可以做成一个包装盒,这些卡纸最多可以做成包装盒的个数为( )A、 B、 C、 D、10. 如图,在中, , , 、分别为、中点,连接、相交于点 , 点在上,且:: , 则四边形的面积为( ) A、 B、 C、 D、11. 我国南宋时期数学家杨辉于年写下的详解九章算法 , 书中记载的图表给出了展开式的系数规律.
A、 B、 C、 D、11. 我国南宋时期数学家杨辉于年写下的详解九章算法 , 书中记载的图表给出了展开式的系数规律.
当代数式的值为时,则的值为( )
A、 B、 C、或 D、或12. 在平面直角坐标系中,直线与抛物线交于、两点,设 , , 则下列结论正确的个数为( ). . 当线段长取最小值时,则的面积为 . 若点 , 则 .
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
13. 在 , , , 四个数中,最小的实数是 .14. 已知为正整数,点在第一象限中,则 .15. 这组数据 , , , , , 的中位数是 .16. 关于的分式方程有增根,则 .17. 如图,已知正方形和正方形 , 点在上,与交于点 , , 正方形的边长为 , 则的长为 .
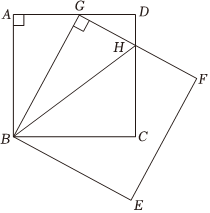 18. 规定:如果两个函数的图象关于轴对称,那么称这两个函数互为“函数”例如:函数与互为“函数”若函数的图象与轴只有一个交点,则它的“函数”图象与轴的交点坐标为 .
18. 规定:如果两个函数的图象关于轴对称,那么称这两个函数互为“函数”例如:函数与互为“函数”若函数的图象与轴只有一个交点,则它的“函数”图象与轴的交点坐标为 .三、解答题(本大题共7小题,共84.0分。)
-
19.(1)、计算: .(2)、求不等式组的解集.(3)、先化简,再求值 , 其中的值是方程的根.20. 如图,已知等边 , , 为中点以为圆心,适当长为半径画弧,交于点 , 交于点 , 分别以、为圆心,大于为半径画弧,两弧交于点 , 作射线交于点过点作交射线于点 , 连接、 .
 (1)、求证:四边形是菱形.(2)、若 , 求的面积.21. 年全国教育工作会议提出要把开展读书活动作为一件大事来抓,引导学生爱读书,读好书,善读书某校为了推进这项工作,对全校学生一周内平均读书时间进行抽样调查,将调查结果的数据分成、、、、五个等级并绘制成表格和扇形统计图如下.
(1)、求证:四边形是菱形.(2)、若 , 求的面积.21. 年全国教育工作会议提出要把开展读书活动作为一件大事来抓,引导学生爱读书,读好书,善读书某校为了推进这项工作,对全校学生一周内平均读书时间进行抽样调查,将调查结果的数据分成、、、、五个等级并绘制成表格和扇形统计图如下.等级
周平均读书时间单位;小时
人数
 (1)、求统计图表中 , .(2)、已知该校共有名学生,试估计该校每周读书时间至少小时的人数为 .(3)、该校每月末从每个班读书时间在等级的学生中选取名学生参加读书心得交流会,九年级某班共有名男生名女生的读书时间在等级,现从这名学生中选取名参加交流会,用画树状图或列表的方法求该班恰好选出名男生名女生参加交流会的概率.22. 如图,已知等腰 , , 以为直径作交于点 , 过作于点 , 交延长线于点 .
(1)、求统计图表中 , .(2)、已知该校共有名学生,试估计该校每周读书时间至少小时的人数为 .(3)、该校每月末从每个班读书时间在等级的学生中选取名学生参加读书心得交流会,九年级某班共有名男生名女生的读书时间在等级,现从这名学生中选取名参加交流会,用画树状图或列表的方法求该班恰好选出名男生名女生参加交流会的概率.22. 如图,已知等腰 , , 以为直径作交于点 , 过作于点 , 交延长线于点 . (1)、求证:是的切线.(2)、若 , , 求图中阴影部分的面积结果用表示 .23. 如图,正比例函数与反比例函数的图象交于、两点,的横坐标为 , 的纵坐标为 .
(1)、求证:是的切线.(2)、若 , , 求图中阴影部分的面积结果用表示 .23. 如图,正比例函数与反比例函数的图象交于、两点,的横坐标为 , 的纵坐标为 .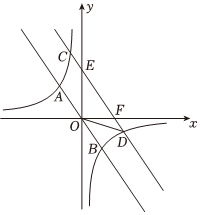 (1)、求反比例函数的表达式.(2)、观察图象,直接写出不等式的解集.(3)、将直线向上平移个单位,交双曲线于、两点,交坐标轴于点、 , 连接、 , 若的面积为 , 求直线的表达式.24. 综合与实践.
(1)、求反比例函数的表达式.(2)、观察图象,直接写出不等式的解集.(3)、将直线向上平移个单位,交双曲线于、两点,交坐标轴于点、 , 连接、 , 若的面积为 , 求直线的表达式.24. 综合与实践.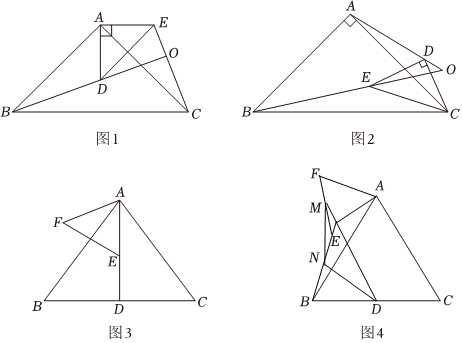 (1)、提出问题如图 , 在和中, , 且 , , 连接 , 连接交的延长线于点 .
(1)、提出问题如图 , 在和中, , 且 , , 连接 , 连接交的延长线于点 .的度数是 .
: .
(2)、类比探究如图 , 在和中, , 且 , , 连接、并延长交于点 .的度数是 ;
: .
(3)、问题解决如图 , 在等边中,于点 , 点在线段上不与重合 , 以为边在的左侧构造等边 , 将绕着点在平面内顺时针旋转任意角度如图 , 为的中点,为的中点.说明为等腰三角形.
求的度数.
25. 在平面直角坐标系中,抛物线经过点和 , 其顶点的横坐标为 . (1)、求抛物线的表达式.(2)、若直线与轴交于点 , 在第一象限内与抛物线交于点 , 当取何值时,使得有最大值,并求出最大值.(3)、若点为抛物线的对称轴上一动点,将抛物线向左平移个单位长度后,为平移后抛物线上一动点在的条件下求得的点 , 是否能与、、构成平行四边形?若能构成,求出点坐标;若不能构成,请说明理由.
(1)、求抛物线的表达式.(2)、若直线与轴交于点 , 在第一象限内与抛物线交于点 , 当取何值时,使得有最大值,并求出最大值.(3)、若点为抛物线的对称轴上一动点,将抛物线向左平移个单位长度后,为平移后抛物线上一动点在的条件下求得的点 , 是否能与、、构成平行四边形?若能构成,求出点坐标;若不能构成,请说明理由.