北师大版数学九年级上册同步练习——第四章 《图形的相似》综合练习(B)
试卷更新日期:2023-07-27 类型:单元试卷
一、选择题(每题3分,共36分)
-
1. 如图,在△ABC中,点D、E分别在边AB、AC上,若DE∥BC, ,DE=6cm,则BC的长为( )
 A、9cm B、12cm C、15cm D、18cm2. 如图,在中,点D、E为边的三等分点,点F、G在边上, , 点H为与的交点.若 , 则的长为( )
A、9cm B、12cm C、15cm D、18cm2. 如图,在中,点D、E为边的三等分点,点F、G在边上, , 点H为与的交点.若 , 则的长为( ) A、1 B、 C、2 D、33. 如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为 , 同时量得小菲与镜子的水平距离为 , 镜子与旗杆的水平距离为 , 则旗杆高度为( )
A、1 B、 C、2 D、33. 如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为 , 同时量得小菲与镜子的水平距离为 , 镜子与旗杆的水平距离为 , 则旗杆高度为( ) A、 B、 C、 D、4. 如图,点在正方形的对角线上,于点 , 连接并延长,交边于点 , 交边的延长线于点 . 若 , , 则( )
A、 B、 C、 D、4. 如图,点在正方形的对角线上,于点 , 连接并延长,交边于点 , 交边的延长线于点 . 若 , , 则( ) A、 B、 C、 D、5. 如图,在矩形中, , , 点E、F分别为、的中点,、相交于点G,过点E作 , 交于点H,则线段的长度是( )
A、 B、 C、 D、5. 如图,在矩形中, , , 点E、F分别为、的中点,、相交于点G,过点E作 , 交于点H,则线段的长度是( )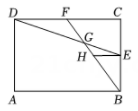 A、 B、1 C、 D、6. 西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则y关于x的函数表达式为( )
A、 B、1 C、 D、6. 西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则y关于x的函数表达式为( )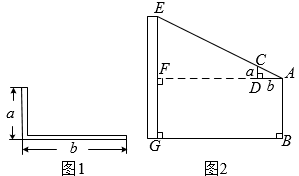 A、 B、 C、 D、7. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )
A、 B、 C、 D、7. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )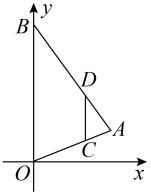 A、4 B、5 C、6 D、78. 如图,点、、、在网格中小正方形的顶点处,与相交于点 , 小正方形的边长为1,则的长等于( )
A、4 B、5 C、6 D、78. 如图,点、、、在网格中小正方形的顶点处,与相交于点 , 小正方形的边长为1,则的长等于( ) A、2 B、 C、 D、9. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
A、2 B、 C、 D、9. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中,O为原点,OA=OB= , 点C为平面内一动点,BC= , 连接AC,点M是线段AC上的一点,且满足CM∶MA=1∶2.当线段OM取最大值时,点M的坐标是( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,O为原点,OA=OB= , 点C为平面内一动点,BC= , 连接AC,点M是线段AC上的一点,且满足CM∶MA=1∶2.当线段OM取最大值时,点M的坐标是( )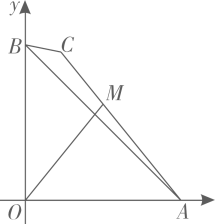 A、( , ) B、( , ) C、( , ) D、( , )11. 如图,在正方形中,点E是上一点,延长至点F,使 , 连结 , 交于点K,过点A作 , 垂足为点H,交于点G,连结 . 下列四个结论:①;②;③;④ . 其中正确结论的个数为( )
A、( , ) B、( , ) C、( , ) D、( , )11. 如图,在正方形中,点E是上一点,延长至点F,使 , 连结 , 交于点K,过点A作 , 垂足为点H,交于点G,连结 . 下列四个结论:①;②;③;④ . 其中正确结论的个数为( )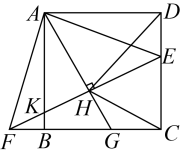 A、1个 B、2个 C、3个 D、4个12. 如图,已知 , , ,点E为射线 上一个动点,连接 ,将 沿 折叠,点B落在点 处,过点 作 的垂线,分别交 , 于M , N两点,当 为线段 的三等分点时, 的长为( )
A、1个 B、2个 C、3个 D、4个12. 如图,已知 , , ,点E为射线 上一个动点,连接 ,将 沿 折叠,点B落在点 处,过点 作 的垂线,分别交 , 于M , N两点,当 为线段 的三等分点时, 的长为( )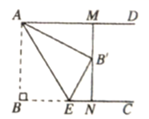 A、 B、 C、 或 D、 或
A、 B、 C、 或 D、 或二、填空题(每空3分,共18分)
-
13. 如图,在中,以点为圆心,任意长为半径作弧,分别交 , 于点 , ;分别以点 , 为圆心,大于的长为半径作弧,两弧交于点;作射线交于点 , 若 , , 的面积为 , 则的面积为 .
 14. 如图1,在中, , , , D是上一点,且 , 过点D作交于E,将绕A点顺时针旋转到图2的位置.则图2中的值为 .
14. 如图1,在中, , , , D是上一点,且 , 过点D作交于E,将绕A点顺时针旋转到图2的位置.则图2中的值为 .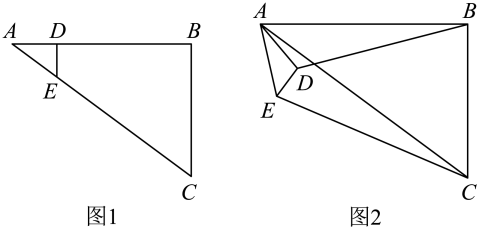 15. 如图,在菱形中,点E,F,G,H分别是 , , , 上的点,且 , 若菱形的面积等于24, , 则 .
15. 如图,在菱形中,点E,F,G,H分别是 , , , 上的点,且 , 若菱形的面积等于24, , 则 . 16. 如图,三角形纸片中, , 分别沿与平行的方向,从靠近A的AB边的三等分点剪去两个角,得到的平行四边形纸片的周长是 .
16. 如图,三角形纸片中, , 分别沿与平行的方向,从靠近A的AB边的三等分点剪去两个角,得到的平行四边形纸片的周长是 . 17. 如图,在中, , 点分别在边 , 上,连接 , 已知点和点关于直线对称.设 , 若 , 则(结果用含的代数式表示).
17. 如图,在中, , 点分别在边 , 上,连接 , 已知点和点关于直线对称.设 , 若 , 则(结果用含的代数式表示). 18. 如图,在正方形中, , 延长至 , 使 , 连接 , 平分交于 , 连接 , 则的长为 .
18. 如图,在正方形中, , 延长至 , 使 , 连接 , 平分交于 , 连接 , 则的长为 .
三、解答题(共7题,共66分)
-
19. 三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G是 的重心.求证: .
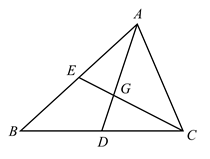 20. 如图,点E、F、G、H分别是各边的中点,连接相交于点M,连接相交于点N.
20. 如图,点E、F、G、H分别是各边的中点,连接相交于点M,连接相交于点N.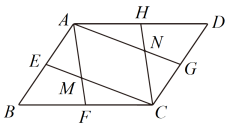 (1)、求证:四边形是平行四边形;(2)、若的面积为4,求的面积.21. 如图,中,点E是的中点,连接并延长交的延长线于点F.
(1)、求证:四边形是平行四边形;(2)、若的面积为4,求的面积.21. 如图,中,点E是的中点,连接并延长交的延长线于点F. (1)、求证:;(2)、点G是线段上一点,满足 , 交于点H,若 , 求的长.22. 如图,点为线段上一点,分别以为等腰三角形的底边,在的同侧作等腰和等腰 , 且 . 在线段上取一点 , 使 , 连接 .
(1)、求证:;(2)、点G是线段上一点,满足 , 交于点H,若 , 求的长.22. 如图,点为线段上一点,分别以为等腰三角形的底边,在的同侧作等腰和等腰 , 且 . 在线段上取一点 , 使 , 连接 . (1)、如图1,求证:;(2)、如图2,若的延长线恰好经过的中点 , 求的长.23. 【问题呈现】
(1)、如图1,求证:;(2)、如图2,若的延长线恰好经过的中点 , 求的长.23. 【问题呈现】和都是直角三角形, , 连接 , , 探究 , 的位置关系.
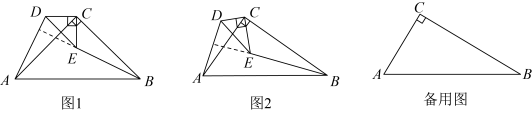 (1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】
(1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】当时,将绕点C旋转,使三点恰好在同一直线上,求的长.
24. 综合与实践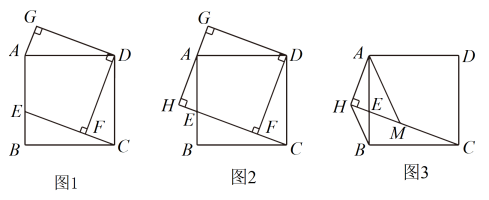 (1)、【思考尝试】
(1)、【思考尝试】数学活动课上,老师出示了一个问题:如图1,在矩形ABCD中,E是边上一点,于点F, , , . 试猜想四边形的形状,并说明理由;
(2)、【实践探究】小睿受此问题启发,逆向思考并提出新的问题:如图2,在正方形中,E是边上一点,于点F,于点H,交于点G,可以用等式表示线段 , , 的数量关系,请你思考并解答这个问题;
(3)、【拓展迁移】小博深入研究小睿提出的这个问题,发现并提出新的探究点:如图3,在正方形中,E是边上一点,于点H,点M在上,且 , 连接 , , 可以用等式表示线段 , 的数量关系,请你思考并解答这个问题.
25. (1)、如图1,在矩形中,点 , 分别在边 , 上, , 垂足为点 . 求证: .(2)、【问题解决】
(1)、如图1,在矩形中,点 , 分别在边 , 上, , 垂足为点 . 求证: .(2)、【问题解决】如图2,在正方形中,点 , 分别在边 , 上, , 延长到点 , 使 , 连接 . 求证: .
(3)、【类比迁移】如图3,在菱形中,点 , 分别在边 , 上, , , , 求的长.