2023-2024学年北师大版数学九年级上册1.3正方形的性质与判定(提升卷)
试卷更新日期:2023-07-27 类型:同步测试
一、选择题
-
1. 如图,在正方形中, , E,F分别为边的中点,连接 , 点G,H分别为的中点,连接 , 则的长为( )
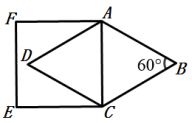
 A、 B、1 C、 D、22. 如图,在正方形中, , 为对角线上与点 , 不重合的一个动点,过点作于点 , 于点 , 连接 , .给出下列结论:①;②;③;④的最小值为3.其中正确的结论有( )
A、 B、1 C、 D、22. 如图,在正方形中, , 为对角线上与点 , 不重合的一个动点,过点作于点 , 于点 , 连接 , .给出下列结论:①;②;③;④的最小值为3.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个3. 已知:正方形中,对角线、相交于点 , 的角平分线交于点 , 交于点 , , 则( )
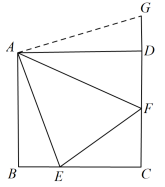
A、1个 B、2个 C、3个 D、4个3. 已知:正方形中,对角线、相交于点 , 的角平分线交于点 , 交于点 , , 则( ) A、 B、 C、 D、4. 对角线长为4cm的正方形其边长为( )A、2cm B、cm C、4cm D、cm5. 如图,在正方形ABCD中,AB=4,点M在CD的边上,且DM=1,△AEM与△ADM关于AM所在的直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为( )
A、 B、 C、 D、4. 对角线长为4cm的正方形其边长为( )A、2cm B、cm C、4cm D、cm5. 如图,在正方形ABCD中,AB=4,点M在CD的边上,且DM=1,△AEM与△ADM关于AM所在的直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为( ) A、3 B、2 C、5 D、6. 下列判断中错误的是( )A、四个角相等的四边形是矩形 B、对角线互相垂直平分的四边形是正方形 C、对角线互相垂直的平行四边形是菱形 D、两组对边分别平行的四边形是平行四边形7. 如图,点E是正方形的边上一点,把绕点A顺时针旋转到位置.若四边形的面积为36, , 则的长为( )
A、3 B、2 C、5 D、6. 下列判断中错误的是( )A、四个角相等的四边形是矩形 B、对角线互相垂直平分的四边形是正方形 C、对角线互相垂直的平行四边形是菱形 D、两组对边分别平行的四边形是平行四边形7. 如图,点E是正方形的边上一点,把绕点A顺时针旋转到位置.若四边形的面积为36, , 则的长为( ) A、 B、 C、6 D、8. 下列命题中,真命题是( )A、对角线互相垂直的四边形是菱形 B、对角线互相垂直平分的四边形是正方形 C、四条边相等的四边形是矩形 D、有一组对边平行且相等的四边形是平行四边形9. 【教材呈现】下图是北师大版九年级上册数学教材第25页第4题内容的变式.如图,三个边长相同的正方形重叠在一起,、是其中两个正方形的中心,阴影部分的面积和是8,则正方形的边长为( )
A、 B、 C、6 D、8. 下列命题中,真命题是( )A、对角线互相垂直的四边形是菱形 B、对角线互相垂直平分的四边形是正方形 C、四条边相等的四边形是矩形 D、有一组对边平行且相等的四边形是平行四边形9. 【教材呈现】下图是北师大版九年级上册数学教材第25页第4题内容的变式.如图,三个边长相同的正方形重叠在一起,、是其中两个正方形的中心,阴影部分的面积和是8,则正方形的边长为( ) A、2 B、4 C、8 D、10. 如图,四边形是正方形,延长到点 , 使 , 则的度数是( )
A、2 B、4 C、8 D、10. 如图,四边形是正方形,延长到点 , 使 , 则的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 我们规定菱形与正方形接近程度称为“接近度”,设菱形相邻两个内角的度数分别为 , , 将菱形的“接近度”定义为 , 于是越小,菱形越接近正方形.
①若菱形的一个内角为 , 则该菱形的“接近度”为;
②当菱形的“接近度”等于时,菱形是正方形.
 12. 如图,直线l上有三个正方形 , 若的面积分别为9和25,若抛一颗石子,落在阴影部分的概率为.
12. 如图,直线l上有三个正方形 , 若的面积分别为9和25,若抛一颗石子,落在阴影部分的概率为. 13. 如图,正方形中,将边绕着点A旋转,当点B落在边的垂直平分线上的点E处时,的度数为 .
13. 如图,正方形中,将边绕着点A旋转,当点B落在边的垂直平分线上的点E处时,的度数为 . 14. 正方形的对称中心为点 , 若 , 则该正方形的周长为.15. 如图,已知P是正方形ABCD对角线AC上的一点,且AP=AD,则∠CDP的大小是度.
14. 正方形的对称中心为点 , 若 , 则该正方形的周长为.15. 如图,已知P是正方形ABCD对角线AC上的一点,且AP=AD,则∠CDP的大小是度.
三、解答题
-
16. 如图,正方形ABCD中,点P,Q分别为CD,AD边上的点,且DQ=CP,连接BQ,AP.求证:BQ⊥AP.
 17. 如图,在矩形中,点E,F分别在边上, , 且 , 与相交于点G.求证:矩形为正方形;
17. 如图,在矩形中,点E,F分别在边上, , 且 , 与相交于点G.求证:矩形为正方形;