广东省深圳市重点中学2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-07-27 类型:期末考试
一、选择题(共10小题,满分30分,每小题3分)
-
1. 下列方程中,是一元二次方程的是( )A、 B、 C、 D、2. 下列说法错误的是( )A、菱形的对角线互相垂直且平分 B、矩形的对角线相等 C、有一组邻边相等的四边形是菱形 D、四条边相等的四边形是菱形3. 若是方程的两个根,则( )A、 B、 C、 D、4. 同时抛掷两枚质地均匀的硬币,则出现两个正面朝上的概率是( )A、 B、 C、 D、5.
如图,在房子屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区是( )
 A、△ACE B、△ADF C、△ABD D、四边形BCED6. 从前有一个醉汉拿着竹竿进城,横拿坚拿都进不去,横着比城门宽米,坚着比城门高米,一个聪明人告诉他沿着城门的两对角斜着拿竿,这个醉汉一试,不多不少刚好进去了,求竹竿的长度.若设竹竿长米,则根据题意,可列方程( )A、 B、 C、 D、7. 如图,已知直线a//b//c,若AB=2,BC=3,EF=2.5,则DE=( )
A、△ACE B、△ADF C、△ABD D、四边形BCED6. 从前有一个醉汉拿着竹竿进城,横拿坚拿都进不去,横着比城门宽米,坚着比城门高米,一个聪明人告诉他沿着城门的两对角斜着拿竿,这个醉汉一试,不多不少刚好进去了,求竹竿的长度.若设竹竿长米,则根据题意,可列方程( )A、 B、 C、 D、7. 如图,已知直线a//b//c,若AB=2,BC=3,EF=2.5,则DE=( ) A、 B、 C、 D、8. 如图,D、E分别是的边AB、BC上的点,且 , 若 , 则的值为( )
A、 B、 C、 D、8. 如图,D、E分别是的边AB、BC上的点,且 , 若 , 则的值为( ) A、 B、 C、 D、9. 若关于的一元二次方程有实数根,则可取的最大整数值为( )A、1 B、0 C、-1 D、-210. 如图,在矩形ABCD中,.把AD沿AE折叠,使点恰好落在AB边上的处,再将绕点顺时针旋转 , 得到 , 使得恰好经过的中点.设交AB于点 , 连接.有如下结论:①;②的长度是;③;④.上述结论中,正确的个数有( )
A、 B、 C、 D、9. 若关于的一元二次方程有实数根,则可取的最大整数值为( )A、1 B、0 C、-1 D、-210. 如图,在矩形ABCD中,.把AD沿AE折叠,使点恰好落在AB边上的处,再将绕点顺时针旋转 , 得到 , 使得恰好经过的中点.设交AB于点 , 连接.有如下结论:①;②的长度是;③;④.上述结论中,正确的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(共5小题,满分15分,每小题3分)
-
11. 若关于x的方程的一个根为3,则m的值为 .12. 如图,在平面直角坐标系中,已知A(1,0),B(2,1),D(3,0),△ABC与△DEF位似,原点O是位似中心,则E点的坐标是.
 13. 若一个直角三角形两条直角边的长分别是一元二次方程x2-6x+7=0的两个实数根,则这个直角三角形斜边的长是.14. 如图,在矩形ABCD中,P、Q分别是BC、DC上的点,EF分别是AP、PQ的中点.BC=12,DQ=5,在点P从B移动到C(点Q不动)的过程中,则线段EF=.
13. 若一个直角三角形两条直角边的长分别是一元二次方程x2-6x+7=0的两个实数根,则这个直角三角形斜边的长是.14. 如图,在矩形ABCD中,P、Q分别是BC、DC上的点,EF分别是AP、PQ的中点.BC=12,DQ=5,在点P从B移动到C(点Q不动)的过程中,则线段EF=. 15. 如图,在正方形ABCD中,AB=2,点E是BC边的中点,连接AE,延长EB至点F,使得EF=AE,过点F作FG⊥AE,垂足为M,FG分别交CD、AB于G、N两点,则=.
15. 如图,在正方形ABCD中,AB=2,点E是BC边的中点,连接AE,延长EB至点F,使得EF=AE,过点F作FG⊥AE,垂足为M,FG分别交CD、AB于G、N两点,则=.
三、解答题(共7小题,满分55分)
-
16. 解下列方程:(1)、4x2-8x+1=0(2)、3(x-5)2=2(5-x)17. 某博物馆展厅的俯视示意图如图1所示,嘉淇进入展厅后开始自由参观,每走到一个十字道口,她自己可能直行,也可能向左转或向右转,且这三种可能性均相同.
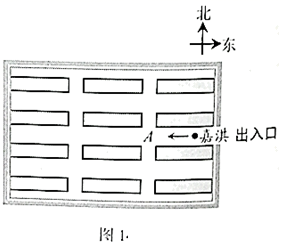
 (1)、求嘉淇走到十字道口 向北走的概率;(2)、补全图2的树状图,并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大.18. 如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列题目.
(1)、求嘉淇走到十字道口 向北走的概率;(2)、补全图2的树状图,并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大.18. 如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列题目. (1)、请在下面方格纸中分别画出它的左视图和俯视图.(2)、图中共有个小正方体.19. 如图,在矩形中,对角线的垂直平分线分别交、、于点、、 , 连接和 .
(1)、请在下面方格纸中分别画出它的左视图和俯视图.(2)、图中共有个小正方体.19. 如图,在矩形中,对角线的垂直平分线分别交、、于点、、 , 连接和 .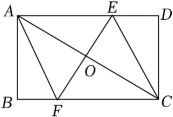 (1)、求证:四边形为菱形;(2)、若 , , 求菱形的周长.20. 某公司2月份销售新上市的A产品20套,由于该产品的经济适用性,销量快速.上升,4月份该公司销售A产品达到45套,并且2月到3月和3月到4月两次的增长率相同.(1)、求该公司销售A产品每次的增长率;(2)、若A产品每套盈利2万元,则平均每月可售30套,为了尽量减少库存,该公司决定采取适当的降价措施,经调查发现,A产品每套每降0.5万元,公司平均每月可多售出20套;若该公司在5月份要获利70万元,则每套A产品需降价多少?21. 如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴、y轴的正半轴上,0A=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP,DA.
(1)、求证:四边形为菱形;(2)、若 , , 求菱形的周长.20. 某公司2月份销售新上市的A产品20套,由于该产品的经济适用性,销量快速.上升,4月份该公司销售A产品达到45套,并且2月到3月和3月到4月两次的增长率相同.(1)、求该公司销售A产品每次的增长率;(2)、若A产品每套盈利2万元,则平均每月可售30套,为了尽量减少库存,该公司决定采取适当的降价措施,经调查发现,A产品每套每降0.5万元,公司平均每月可多售出20套;若该公司在5月份要获利70万元,则每套A产品需降价多少?21. 如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴、y轴的正半轴上,0A=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP,DA.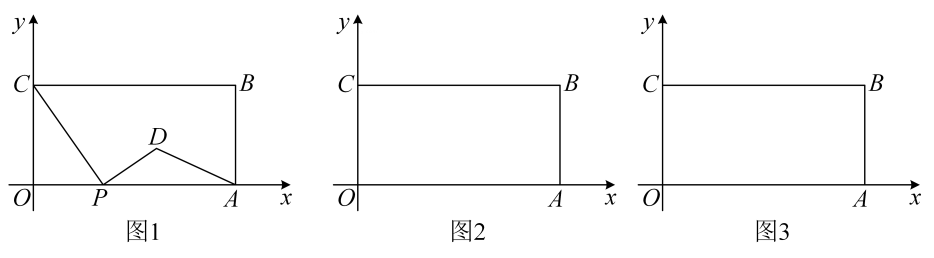 (1)、当t=2时,点D的坐标是;(2)、请用含t的代数式表示出点D的坐标;(3)、在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.若不能,请说明理由.22. 在四边形 中, (E、F分别为边 、 上的动点), 的延长线交 延长线于点M, 的延长线交 延长线于点N.
(1)、当t=2时,点D的坐标是;(2)、请用含t的代数式表示出点D的坐标;(3)、在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.若不能,请说明理由.22. 在四边形 中, (E、F分别为边 、 上的动点), 的延长线交 延长线于点M, 的延长线交 延长线于点N. (1)、如图①,若四边形 是正方形,求证: ;(2)、如图②,若四边形 是菱形,
(1)、如图①,若四边形 是正方形,求证: ;(2)、如图②,若四边形 是菱形,①(1)中的结论是否依然成立?请说明理由;
②若 , ,连接 ,当 时,求 的长.