2023-2024学年北师大版数学九年级上册1.2矩形的性质与判定(提升卷)
试卷更新日期:2023-07-27 类型:同步测试
一、选择题
-
1. 如图,在矩形纸片ABCD中, , , 将AB沿AE翻折,使点B落在处,AE为折痕,再将EC沿EF翻折,使点C恰好落在线段上的点处,EF为折痕,连接 . 若 , 则的值为( )
 A、 B、 C、 D、2. 如图,点P是 中斜边AC(不与A,C重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,点O是MN的中点,若AB=6;BC=8,当点P在AC上运动时,则BO的最小值是( )
A、 B、 C、 D、2. 如图,点P是 中斜边AC(不与A,C重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,点O是MN的中点,若AB=6;BC=8,当点P在AC上运动时,则BO的最小值是( ) A、1.5 B、2 C、2.4 D、2.53. 在数学拓展课《折叠矩形纸片》上,小林发现折叠矩形纸片ABCD可以进行如下操作:①把△ABF翻折,点B落在C边上的点E处,折痕为AF , 点F在BC边上;②把△ADH翻折,点D落在AE边上的点G处,折痕为AH , 点H在CD边上,若AD=6,CD=10,则 =( )
A、1.5 B、2 C、2.4 D、2.53. 在数学拓展课《折叠矩形纸片》上,小林发现折叠矩形纸片ABCD可以进行如下操作:①把△ABF翻折,点B落在C边上的点E处,折痕为AF , 点F在BC边上;②把△ADH翻折,点D落在AE边上的点G处,折痕为AH , 点H在CD边上,若AD=6,CD=10,则 =( )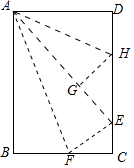 A、 B、 C、 D、4. 如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE= AC,连接CE、OE,连接AE交OD于点F,若AB=2,∠ABC=60° , 则AE的长为( )
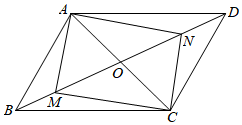
A、 B、 C、 D、4. 如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE= AC,连接CE、OE,连接AE交OD于点F,若AB=2,∠ABC=60° , 则AE的长为( )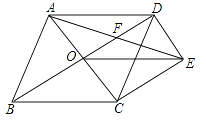 A、 B、 C、 D、5. 如图,在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
A、 B、 C、 D、5. 如图,在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
 A、若AD⊥BC,则四边形AEDF是矩形 B、若BD=CD,则四边形AEDF是菱形 C、若AD垂直平分BC,则四边形AEDF是矩形 D、若AD平分∠BAC,则四边形AEDF是菱形6. 如图,四条线段的长分别为9,5,x、1(其中x为正实数),用它们拼成两个相似的直角三角形,且AB与CD是其中的两条线段,则x可取值的个数为( )
A、若AD⊥BC,则四边形AEDF是矩形 B、若BD=CD,则四边形AEDF是菱形 C、若AD垂直平分BC,则四边形AEDF是矩形 D、若AD平分∠BAC,则四边形AEDF是菱形6. 如图,四条线段的长分别为9,5,x、1(其中x为正实数),用它们拼成两个相似的直角三角形,且AB与CD是其中的两条线段,则x可取值的个数为( ) A、1个 B、3个 C、6个 D、9个7. 如图,四边形ABCD的对角线AC与BD相交于点O,下列条件中,能判定四边形ABCD是矩形的是( )
A、1个 B、3个 C、6个 D、9个7. 如图,四边形ABCD的对角线AC与BD相交于点O,下列条件中,能判定四边形ABCD是矩形的是( ) A、AB∥DC,AB=CD B、AB∥CD,AD∥BC C、AC=BD,AC⊥BD D、OA=OB=OC=OD8. 如图,矩形中,对角线交于点O,若 , , 则长为( )
A、AB∥DC,AB=CD B、AB∥CD,AD∥BC C、AC=BD,AC⊥BD D、OA=OB=OC=OD8. 如图,矩形中,对角线交于点O,若 , , 则长为( ) A、 B、4 C、3 D、59. 如图,在矩形 中, , 相交于点 , 平分交于 , 若 , 则的度数为( )
A、 B、4 C、3 D、59. 如图,在矩形 中, , 相交于点 , 平分交于 , 若 , 则的度数为( ) A、 B、 C、 D、10. 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
A、 B、 C、 D、10. 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )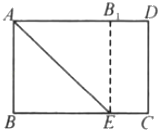 A、2cm B、4cm C、6cm D、1cm
A、2cm B、4cm C、6cm D、1cm二、填空题
-
11. 如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C,D分别落在边BC下方的点C′,D′处,且点C′,D′,B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为(用含t的代数式表示).
 12. 如图,在矩形 中,对角线 , 交于点 , 点 是线段 上一点,若 , , 则 .
12. 如图,在矩形 中,对角线 , 交于点 , 点 是线段 上一点,若 , , 则 . 13. 如图,在矩形ABCD中,E,F分别是AD,AB的中点,若AC=4,则EF的长是.
13. 如图,在矩形ABCD中,E,F分别是AD,AB的中点,若AC=4,则EF的长是. 14. 在矩形中,作的平分线交直线于点E,则是度.15. 如图,在矩形中, , 对角线的长为5,作的垂直平分线交于点 , 连接 , 则的周长为 .
14. 在矩形中,作的平分线交直线于点E,则是度.15. 如图,在矩形中, , 对角线的长为5,作的垂直平分线交于点 , 连接 , 则的周长为 .
三、解答题
-
16. 如图,矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N,证明:△ABN≌△MAD;
 17. 如图,在平行四边形ABCD中,DE⊥AB,点F在AB的延长线上,且CF⊥AB.
17. 如图,在平行四边形ABCD中,DE⊥AB,点F在AB的延长线上,且CF⊥AB.求证:四边形CDEF是矩形.