2023-2024学年北师大版数学九年级上册1.1菱形的性质与判定(培优卷)
试卷更新日期:2023-07-27 类型:同步测试
一、选择题
-
1. 如图,在▱ABCD中,O为AC的中点,经过点O的直线交AD于E交BC于F,连接AF、CE,下列选项可以使四边形AFCE是菱形的为( )
 A、OE=OF B、AE=CF C、EF⊥AC D、EF=AC2. 如图,点E、F、G、H分别是四边形ABCD四条边的中点,要使四边形EFGH为菱形,四边形ABCD应具备的条件是( )
A、OE=OF B、AE=CF C、EF⊥AC D、EF=AC2. 如图,点E、F、G、H分别是四边形ABCD四条边的中点,要使四边形EFGH为菱形,四边形ABCD应具备的条件是( ) A、一组对边平行而另一组对边不平行 B、对角线相等 C、对角线互相垂直 D、对角线互相平分3. 如图,在菱形中,对角线 , 分别为16和12,于点E,则( )
A、一组对边平行而另一组对边不平行 B、对角线相等 C、对角线互相垂直 D、对角线互相平分3. 如图,在菱形中,对角线 , 分别为16和12,于点E,则( ) A、 B、 C、10 D、84. 如图,在菱形中, , 则菱形的周长是( )
A、 B、 C、10 D、84. 如图,在菱形中, , 则菱形的周长是( )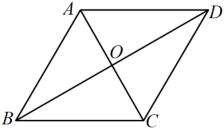 A、 B、 C、 D、5. 如图,菱形对角线交点与坐标原点重合,点 , 则点的坐标为( )
A、 B、 C、 D、5. 如图,菱形对角线交点与坐标原点重合,点 , 则点的坐标为( )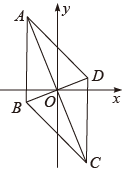 A、 B、 C、 D、6. 如图,菱形ABCD中,∠BAD=60°,AC、BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC,AD于点F、G,连接OG、AE.则下列结论:①OG=AB; ②四边形ABDE是菱形;③S四边形ODGF=S△ABF;其中正确的是( )
A、 B、 C、 D、6. 如图,菱形ABCD中,∠BAD=60°,AC、BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC,AD于点F、G,连接OG、AE.则下列结论:①OG=AB; ②四边形ABDE是菱形;③S四边形ODGF=S△ABF;其中正确的是( ) A、①② B、①③ C、②③ D、①②③7. 如图,在菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论:①OG= AB②与△DEG全等的三角形共有5个:③四边形ODEG与四边形OBAG面积相等:④由点A、B、D、E构成的四边形是菱形。其中一定成立的是( )
A、①② B、①③ C、②③ D、①②③7. 如图,在菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论:①OG= AB②与△DEG全等的三角形共有5个:③四边形ODEG与四边形OBAG面积相等:④由点A、B、D、E构成的四边形是菱形。其中一定成立的是( ) A、①③④ B、①②③ C、①②④ D、②③④8. 如图,小华剪了两条宽为 的纸条,交叉叠放在一起,且它们较小的交角为 ,则它们重叠部分的面积为( )
A、①③④ B、①②③ C、①②④ D、②③④8. 如图,小华剪了两条宽为 的纸条,交叉叠放在一起,且它们较小的交角为 ,则它们重叠部分的面积为( ) A、1 B、2 C、 D、9. 如图,菱形ABCD中的边长为1,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,B′C′交CD于点E,连接AE,CC′,则下列结论:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四边形AB′ED的周长为 +2.其中符合题意结论的个数是( )
A、1 B、2 C、 D、9. 如图,菱形ABCD中的边长为1,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,B′C′交CD于点E,连接AE,CC′,则下列结论:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四边形AB′ED的周长为 +2.其中符合题意结论的个数是( ) A、1 B、2 C、3 D、410. 如图,已知菱形ABCD的周长为16,面积为 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
A、1 B、2 C、3 D、410. 如图,已知菱形ABCD的周长为16,面积为 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )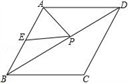 A、2 B、2 C、4 D、4
A、2 B、2 C、4 D、4二、填空题
-
11. 在菱形ABCD中, , ,点P是射线BC上一动点,(不与B,C重合),连接PA,PD,当 是等腰三角形时,BP的长为 .12. 如图,在边长为10的菱形 中,对角线 ,点O是线段 上的动点, 于E, 于F.则 .
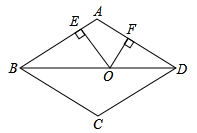 13. 如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边BC上的一个动点,EG=EF,且∠GEF=60°,则GB+GC的最小值为.
13. 如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边BC上的一个动点,EG=EF,且∠GEF=60°,则GB+GC的最小值为.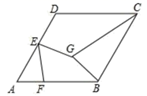 14. 如图,四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相较于点O,点E在AC上,若OE=2 ,则CE的长为
14. 如图,四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相较于点O,点E在AC上,若OE=2 ,则CE的长为 15. 如图,已知四边形是平行四边形,从① , ② , ③中选择一个作为条件,补充后使四边形成为菱形,则应选择(填序号).
15. 如图,已知四边形是平行四边形,从① , ② , ③中选择一个作为条件,补充后使四边形成为菱形,则应选择(填序号).
三、解答题
-
16. 如图,点E是菱形ABCD的边BC延长线上一点,AC是对角线,∠BAC:∠ACE=2:7,求∠B的度数.
 17. 如图,四边形是菱形,于点E,于点F.求证: .
17. 如图,四边形是菱形,于点E,于点F.求证: . 18. 如图,已知矩形ABCD,连接AC,EF垂直平分AC于点O,分别交AD、BC于点E、点F,连接FC.
18. 如图,已知矩形ABCD,连接AC,EF垂直平分AC于点O,分别交AD、BC于点E、点F,连接FC.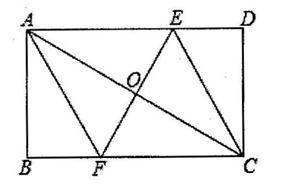 (1)、求证:四边形AECF是菱形;(2)、若△CEF与△CED的面积比为3∶1,且AB=4,求四边形AECF的面积.19. 在菱形ABCD中,∠ABC=60°,P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点P的位置变化而变化.
(1)、求证:四边形AECF是菱形;(2)、若△CEF与△CED的面积比为3∶1,且AB=4,求四边形AECF的面积.19. 在菱形ABCD中,∠ABC=60°,P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点P的位置变化而变化.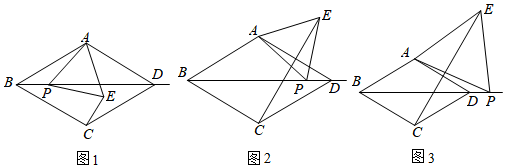 (1)、问题提出
(1)、问题提出
如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系是 , CE与CB的位置关系是 .(2)、如图2,当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由.(3)、问题解决
如图3,连湖公园有一块观赏园林区,其形状是一个边长为20m的菱形ABCD,其中∠ABC=60°,对角线BD是一条花间小径,现计划在BD延长线上(包括D点)取点P,以AP为边长修建一个等边△APE的娱乐区,放置各类运动娱乐设施,从娱乐区顶点E再修一条直直的小路BE,为了让游客们更轻松愉快地游玩,园区还计划在BE中点处设置一个直饮水点F,求饮水点F到C点的最短距离.20. 如图,矩形 中, , ,点 是对角线 的中点,过点 的直线分别交 、 边于点 、 . (1)、求证:四边形 是平行四边形;(2)、当 时,求四边形 的面积.
(1)、求证:四边形 是平行四边形;(2)、当 时,求四边形 的面积.