2023-2024学年北师大版数学九年级上册1.1菱形的性质与判定（提升卷）

试卷更新日期：2023-07-27 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在△ABC中，AD⊥BC于D，E，F分别是AB，AC的中点，连接DE，DF，当△ABC满足下列哪个条件时，四边形AEDF为菱形（　　）

A、AB＝AC B、∠B＝∠A C、BD＝DF D、DE⊥DF

查看试题解析
2. 矩形具有而菱形不一定具有的性质是（）

A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、邻边相等

查看试题解析
3. 如图，某同学剪了两条宽均为 $\sqrt{3}$ 的纸条，交叉叠放在一起，且它们的交角为60°，则它们重叠部分的面积为（）．

A、3 B、 $2 \sqrt{3}$ C、 $3 \sqrt{6}$ D、6

查看试题解析
4. 如图，在 $▱ A B C D$ 中，对角线AC与BD相交于点O，如果添加一个条件，可推出 $▱ A B C D$ 是菱形，那么这个条件可以是（）

A、 $A B = A C$ B、 $A C = B D$ C、 $A C ⊥ B D$ D、 $A B ⊥ A C$

查看试题解析
5. 菱形ABCD的两条对角线AC＝8cm，BD＝6cm，那么菱形的边长是（）

A、6cm B、5cm C、4cm D、8cm

查看试题解析
6. 下列是关于某个四边形的三个结论：①它的对角线互相垂直；②它是一个正方形；③它是一个菱形．下列推理过程正确的是（）

A、由②推出③，由③推出① B、由①推出②，由②推出③ C、由③推出①，由①推出③ D、由①推出③，由③推出②

查看试题解析
7. 如图，在菱形 $A B C D$ 中，点 $E$ 是 $A B$ 的中点，点 $F$ 是 $A C$ 的中点，连接 $E F$ ，如果 $E F = 4$ ，那么菱形 $A B C D$ 的周长为（）

A、4 B、8 C、16 D、32

查看试题解析
8. 如图，两张等宽的纸条交叉叠放在一起，重合部分构成一个四边形 $A B C D$ ，在其中一张纸条转动的过程中，下列结论一定成立的是（　　）

A、 $A D = C D$ B、四边形 $A B C D$ 面积不变 C、 $A C = B D$ D、四边形 $A B C D$ 周长不变

查看试题解析
9. 如图，矩形ABCD的对角线AC、BD相交于点O，∠AOB=120°， $C E ∥ B D$ ， $D E ∥ A C$ ，若AD=2，则四边形CODE的周长为（）

A、12 B、10 C、8 D、4

查看试题解析
10. 如图，在菱形 $A B C D$ 中， $A C$ 与 $B D$ 相交于点O， $B C$ 的垂直平分线 $E F$ 分别交 $B C$ ， $A C$ 于点E，F，连接 $D F$ ，若 $∠ B C D = 70 °$ ，则 $∠ A D F$ 的度数是（）

A、60° B、75 C、80° D、110°

查看试题解析

二、填空题

11. 如图，在菱形 $A B C D$ 中， $∠ A B C = 60 °$ ， $A B = 4$ ， E，F分别是边 $B C$ 和对角线 $B D$ 上的动点，且 $B E = D F$ ，则 $A E + A F$ 的最小值为.

查看试题解析
12. 如图，菱形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点 $O$ ，按下列步骤作图：
①分别以点 $C$ ， $D$ 为圆心，大于 $\frac{1}{2}$ $C D$ 的长为半径画弧，两弧的交点分别为点 $E$ ， $F$ ；
②过点 $E$ ， $F$ 作直线 $E F$ ，交 $C D$ 于点 $P$ ；
③连接 $O P$ .若 $O P = 1.5$ ，则菱形 $A B C D$ 的周长为.

查看试题解析
13. 如图，在菱形 $A B C D$ 中，对角线 $A C$ ， $B D$ 的交点为 $O$ ， $A C = 6$ ， $C D = 5$ .若点 $E$ 在 $B C$ 上，且 $A E ⊥ B C$ ，则 $A E$ 的长为.

查看试题解析
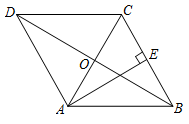14. 如图，菱形ABCD的对角线AC，BD相交于点O，过点D作DH⊥BC于点H，连接OH，若OA＝4， $S_{菱形 A B C D} ＝ 24$ ，则OH的长为．

查看试题解析
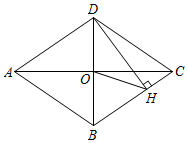15. 中国结，象征着中华民族的历史文化与精致．小明家有一中国结挂饰，他想求两对边的距离，利用所学知识抽象出如图所示的菱形ABCD，测得 $B D = 12 c m$ ， $A C = 16 c m$ ，直线 $E F ⊥ A B$ 交两对边与E、F，则EF的长为cm．

查看试题解析

三、解答题

16. 已知：如图，在菱形 $A B C D$ 中，E.F分别是边 $A B$ 和 $B C$ 上的点，且 $∠ A D E = ∠ C D F$ ，求证： $B E = B F$ .

查看试题解析
17. 如图，在菱形 $A B C D$ 中，分别延长 $A B$ 、 $A D$ 到E、F，使得 $B E = D F$ ，连接 $E C$ 、 $F C$ .求证： $E C = F C$ .

查看试题解析
18. 如图，菱形 $A B C D$ 中， $C E ⊥ A B$ 交 $A B$ 于点E， $C F ⊥ A D$ 交 $A D$ 于点F．
求证： $A E = A F$ ．

查看试题解析
19. 如图，已知△ABC中，D是AC的中点，过点D作DE⊥AC交BC于点E，过点A作AF∥BC交DE于点F，连接AE，CF.求证：四边形AECF是菱形.

查看试题解析
20. 如图，在 $▱ A B C D$ 中， $D E ⊥ A B ， D F ⊥ B C ， D E = D F$ ．求证： $▱ A B C D$ 是菱形．

查看试题解析