湖北省恩施市2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-07-27 类型：期末考试

进入出卷网下载

一、单选题（本大题共12个小题，每小题3分，共36分）

1. 若代数式 $\sqrt{x - 2}$ 有意义，则实数x的取值范围是（）

A、 $x > 2$ B、 $x \geq 2$ C、 $x < 2$ D、 $x \leq 2$

查看试题解析
2. 下列图形中不能表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
3. 下列各组数中，以它们为边长的线段不能构成直角三角形的是（）

A、3，4，5 B、 $\sqrt{5}$ ， $\sqrt{6}$ ， $\sqrt{7}$ C、5，12，13 D、1， $\sqrt{2}$ ， $\sqrt{3}$

查看试题解析
4. 如图所示，在 $▱ A B C D$ 中，对角线 $A C 、 B D$ 交于点O，下列式子中一定成立的是（）

A、 $A C ⊥ B D$ B、 $O A = O C$ C、 $A C = B D$ D、 $A O = O D$

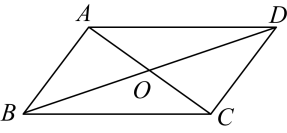查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{3} \times \sqrt{2} = 6$ C、 $\sqrt{8} \div \sqrt{2} = 4$ D、 $\sqrt{12} - \sqrt{3} = \sqrt{3}$

查看试题解析
6. 把直线 $y = - x + 3$ 向上平移 $m (0 < m < 1)$ 个单位后，与直线 $y = 2 x + 4$ 的交点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 下表记录了甲、乙、丙、丁四名跳高运动员最近10次训练成绩（单位：cm）的平均数与方差：

甲
乙
丙
丁
平均数
181
183
183
181
方差
1.6
3.4
1.6
3.4
要选择一名成绩好且发挥稳定的同学参加比赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 若实数a、b、c满足 $a + b + c = 0$ ，且 $a < b < c$ ，则函数 $y = - c x - a$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
9. 下图是在北京召开的国际数学家大会的会标，它是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形，若小正方形的面积为8，每个直角三角形比小正方形的面积均小1，则每个小直角三角形的周长是（）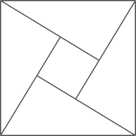

A、 $5 + \sqrt{13}$ B、 $9 + \sqrt{26}$ C、 $10 + \sqrt{13}$ D、14

查看试题解析
10. 点P从某四边形的一个顶点A出发，沿着该四边形的边逆时针匀速运动一周．设点P运动的时间为x，点P与该四边形对角线交点的距离为y，表示y与x的函数关系的大致图像如图所示，则该四边形可能是（）

A、 B、 C、 D、

查看试题解析
11. 如图，在 $△ A B C$ 中，点D是边BC上的点（与B，C两点不重合），过点D作 $D E ∥ A C$ ， $D F ∥ A B$ ，分别交AB，AC于E，F两点，下列说法正确的是（）

A、若 $A C ⊥ B C$ ，则四边形AEDF是矩形 B、若 $B D = C D$ ，则四边形AEDF是菱形 C、若AD垂直平分BC，则四边形AEDP是矩形 D、若AD平分 $∠ B A C$ ，则四边形AEDF是菱形

查看试题解析
12. 如图，正方形ABCD的边长为4，点E在边AD上运动，点F在边CD上运动，运动过程中EF的长度保持不变，且 $E F = 2$ ．若M是EF的中点，P是边AB上的动点，则 $P C + P M$ 的最小值为（）

A、 $4 \sqrt{5} - 1$ B、 $8 \sqrt{5} - 1$ C、 $4 \sqrt{2} - 1$ D、 $8 \sqrt{5} - 2$

查看试题解析

二、填空题（本大题共4个小题，每小题3分，共12分）

13. 若一组数据1，3，x，5，4，6的平均数是4，则这组数据的中位数是.

查看试题解析
14. 已知点 $A (m ， 2)$ ， $B (n ， - 3)$ 在一次函数 $y = (- k^{2} - 1) x + b$ 的图象上，则m，n的大小关系是mn．（填“>”，“<”或“=”）

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ，点D是BC的中点，连接AD．分别以点A，C为圆心，AD的长为半径在 $△ A B C$ 外画弧，两弧交于点E，连接AE，CE，过点D作 $D F ⊥ C E$ 于点F．若 $A B = 12$ ， $A C = 16$ ，则DF的长为．

查看试题解析
16. 如图，已知直线 $l_{1} ： y = - x + 2$ 与 $l_{2} ： y = \frac{1}{2} x + \frac{1}{2}$ ，过直线 $l_{1}$ 与x轴的交点 $P_{1}$ 作x轴的垂线交 $l_{2}$ 于 $Q_{1}$ ，过 $Q_{1}$ 作x轴的平行线交 $l_{1}$ 于 $P_{2}$ ，再过 $P_{2}$ 作x轴的垂线交 $l_{2}$ 于 $Q_{2}$ ，过 $Q_{2}$ 作x轴的平行线交 $l_{1}$ 于 $Q_{3}$ ， …，这样一直作下去，可在直线 $l_{1}$ 上继续得到点 $P_{4}$ ， $P_{5}$ ， …， $P_{n}$ ， …设点 $P_{n}$ 的横坐标为 $x_{n}$ ，则 $x_{n + 1}$ 与 $x_{n}$ 的数量关系是．

查看试题解析

三、解答题（共72分）

17. 计算：

(1)、 $\sqrt{8} - \sqrt{\frac{1}{2}} + \sqrt{32}$ ；

(2)、 ${(2 \sqrt{2})}^{2} - (1 + \sqrt{2}) (1 - \sqrt{2})$ ．

查看试题解析
18. 在数学课上，老师提出问题：如何用尺规作一个矩形？
小华的设计如下：
①如图，任取一点O，过点O作直线 $l_{1}$ ， $l_{2}$ ；
②以O为圆心，任意长为半径作圆，与直线 $l_{1}$ 交于点A，C，与直线 $l_{2}$ 交于点B，D；
③连接AB，BC，CD，DA．
所以，四边形ABCD即为所求作的矩形．
老师说小华的设计是正确的，请你根据小华的设计完成以下问题：

(1)、在作图区内，使用直尺和圆规，补全图形（保留作图痕迹）；

(2)、将证明四边形ABCD是矩形的过程书写完整．

查看试题解析
19. 小明计划制作一架小型飞机模型，如图的四边形材料是飞机垂直尾翼，小明测量发现 $A B = 13 c m$ ， $A D = 5 c m$ ， $∠ D B C = 90 °$ ， $B C = 16 c m$ ， $C D = 20 c m$ ．根据设计要求需保证
$A D ∥ B C$ ．请判断该尾翼是否符合设计要求，并说明理由．

查看试题解析
20. 党的二十大报告提出：传承中华优秀传统文化，满足人民日益增长的精神文化需求，某校积极开展活动，从诗词歌赋、戏剧戏曲、国宝非遗、饮食文化、名人书法五个方面让传统文化“活”起来，在某次竞赛活动中，学校随机抽取部分学生进行知识竞赛，竞赛成绩按以下五组进行整理（得分用x表示）：A： $50 \leq x < 60$ ， B： $60 \leq x < 70$ ， C： $70 \leq x < 80$ ， D： $80 \leq x < 90$ ， E： $90 \leq x \leq 100$ ，并绘制出如下的统计图1和图2．

请根据相关信息，解答下列问题：

(1)、图1中A组所在扇形的圆心角度数为 ▲ °，并将条形统计图补充完整．

(2)、若“ $90 \leq x \leq 100$ ”这一组的数据为：90，96，92，95，93，96，96，95，97，100．求这组数据的众数和中位数．

(3)、若此次竞赛进入初赛后还要进行三轮知识问答，将这三轮知识问答的成绩按20%，30%，50%的比例确定最后得分，得分达到90分及以上可进入决赛，小敏这三轮的成绩分别为86，89，93，问小敏能参加决赛吗？请说明你的理由．

查看试题解析
21. 在平面直角坐标系 $x O y$ 中，直线 $l_{l} ： y = 3 x$ 与直线 $l_{2} ： y = k x + b$ 交于点 $A (a ， 3)$ ，点 $B (2 ， 4)$ 在直线 $l_{2}$ 上．

(1)、求a的值；

(2)、求直线 $l_{2}$ 的解析式；

(3)、直接写出关于x的不等式 $3 x < k x + b$ 的解集．

查看试题解析
22. 如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上， $E F ⊥ A B$ ， $O G ∥ E F$ ．

(1)、判断四边形OEFG的形状，并证明．

(2)、若 $A C = 8$ ， $B D = 6$ ，求四边形OEFG的面积．

查看试题解析
23. 202年FIFA世界杯期间，某商店购进A、B两种品牌的足球进行销售．销售5个A品牌和10个B品牌足球的利润和为700元，销售10个A品牌和5个B品牌足球的利润和为800元．

(1)、求每个A品牌和B品牌足球的销售利润；

(2)、商店计划购进两种品牌足球共100个，设购进A品牌足球x个，两种足球全部销售完共获利y元．
①求y与x之间的函数关系式：（不必写x的取值范围）
②若购进A品牌足球的个数不少于60个，且不超过B品牌足球个数的4倍，求最大利润为多少．

查看试题解析
24. 如图，在平面直角坐标系中，矩形OABC的顶点A，B的坐标分别为 $A (0 ， 2)$ ， $B (4 ， 2)$ ，点D为对角线OB中点，点E在x轴上运动，连接DE，把 $△ O D E$ 沿DE翻折，点O的对应点为点F，连接BF．

(1)、当点F在第四象限时（如图1），求证： $D E ∥ B F$ ．

(2)、当点F落在矩形的某条边上时，求EF的长．

(3)、是否存在点E，使得以D，E，F，B为顶点的四边形是平行四边形？若存在，求点E的坐标；若不存在，请说明理由．

查看试题解析

	甲	乙	丙	丁
平均数	181	183	183	181
方差	1.6	3.4	1.6	3.4