广东省茂名市高州市2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-07-27 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 下面几条线段能构成三角形的是 ( )
A、3,1,5 B、5,12,14 C、7,2,4 D、1,2,33. 下面四幅作品分别代表二十四节气中的“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是A、 B、
B、 C、
C、 D、
D、 4. 2021年是中国共产党建党百年,走过百年光辉历程的中国共产党,成为世界最大的马克思主义执政党.截止2023年6月5日全国共有9518万名中国共产党员,将“9518万”用科学记数法表示应为( )A、 B、 C、 D、5. 如图,点E在AC的延长线上,下列条件不能判断AC∥BD的是( )
4. 2021年是中国共产党建党百年,走过百年光辉历程的中国共产党,成为世界最大的马克思主义执政党.截止2023年6月5日全国共有9518万名中国共产党员,将“9518万”用科学记数法表示应为( )A、 B、 C、 D、5. 如图,点E在AC的延长线上,下列条件不能判断AC∥BD的是( ) A、∠3=∠4 B、∠D=∠DCE C、∠1=∠2 D、∠D+∠ACD=180°6. 将一个球竖直向上抛起,球升到最高点,垂直下落,直到地面.在此过程中,球的高度与下落时间的关系可以用下图中的哪一幅来近似地刻画( )A、
A、∠3=∠4 B、∠D=∠DCE C、∠1=∠2 D、∠D+∠ACD=180°6. 将一个球竖直向上抛起,球升到最高点,垂直下落,直到地面.在此过程中,球的高度与下落时间的关系可以用下图中的哪一幅来近似地刻画( )A、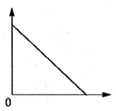 B、
B、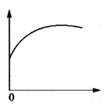 C、
C、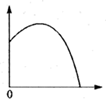 D、
D、 7. 如图,等腰△ABC的周长为16,底边BC= , AB=AC,∠A=36°,线段AB的垂直平分线交AB于点D,交AC于点E,连接BE,则下列说法中错误的是( )
7. 如图,等腰△ABC的周长为16,底边BC= , AB=AC,∠A=36°,线段AB的垂直平分线交AB于点D,交AC于点E,连接BE,则下列说法中错误的是( ) A、是等腰三角形 B、平分 C、△CBE的周长为 , D、△ABE的周长为:8. 有一条直的等宽纸带,按如图折叠时,纸带重叠部分中的∠α=( )
A、是等腰三角形 B、平分 C、△CBE的周长为 , D、△ABE的周长为:8. 有一条直的等宽纸带,按如图折叠时,纸带重叠部分中的∠α=( )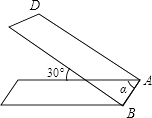 A、30° B、45° C、60° D、75°9. 若x2+(m-3)x+16是完全平方式,则m的值是( )A、-5 B、11 C、-5或11 D、-11或510. 如图,已知与都是等边三角形,点B,C,D在同一条直线上,与相交于点 , 与相交于点 , 与相交于点 , 则下列结论:①;②;③;④是等边三角形,其中正确的个数是( )
A、30° B、45° C、60° D、75°9. 若x2+(m-3)x+16是完全平方式,则m的值是( )A、-5 B、11 C、-5或11 D、-11或510. 如图,已知与都是等边三角形,点B,C,D在同一条直线上,与相交于点 , 与相交于点 , 与相交于点 , 则下列结论:①;②;③;④是等边三角形,其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 已知则=.12. 如图,点D,E分别在线段上,相交于点O, , 要使 , 需添加一个条件是(只需填一个即可).
 13. 若 , , 则的值为 .14. 如图,直线 , ,则 .
13. 若 , , 则的值为 .14. 如图,直线 , ,则 .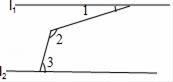 15. 如图,在长方形中, , , 延长到点 , 使 , 连接 , 动点从点出发,以每秒2个单位的速度沿向终点运动,设点的运动时间为秒,当的值为秒时,和全等.
15. 如图,在长方形中, , , 延长到点 , 使 , 连接 , 动点从点出发,以每秒2个单位的速度沿向终点运动,设点的运动时间为秒,当的值为秒时,和全等.
三、解答题
-
16.(1)、计算: .(2)、先化简,再求值: , 其中 .
四、填空题
-
17. 完成下列推理过程:如图,已知 , , 证明: .
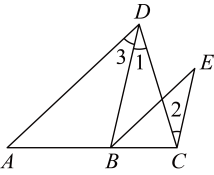
证明:(已知)
∴( )
▲ ( )
(已知)
▲ (等量代换)
∴ ▲ ( )
( ).
五、解答题
-
18. 一个不透明的口袋中装有8个白球和12个红球,每个球除颜色外都相同.(1)、“从口袋里随机摸出一个球是黄球”这一事件是事件;(2)、“一次性摸出9个球,摸到的球中至少有一个红球”这一事件发生的概率为;(3)、从口袋里取走x个红球后,再放入x个白球,并充分摇匀,如果随机摸出白球的概率是 , 求x的值.19. 一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
 (1)、农民自带的零钱是多少?(2)、降价前他每千克西瓜出售的价格是多少?(3)、随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的西瓜?(4)、请问这个水果贩子一共赚了多少钱?20. 如图,点A,B,C,D在同一条直线上, , , .
(1)、农民自带的零钱是多少?(2)、降价前他每千克西瓜出售的价格是多少?(3)、随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的西瓜?(4)、请问这个水果贩子一共赚了多少钱?20. 如图,点A,B,C,D在同一条直线上, , , . (1)、求证:;(2)、若 , 求三角形的面积.21. 把代数式通过配方等手段得到完全平方式,再运用完全平方式的非负性这一性质解决问题,这种解题方法叫做配方法.配方法在代数式求值,解方程,最值问题等都有广泛的应用.如利用配方法求最小值,求的最小值.
(1)、求证:;(2)、若 , 求三角形的面积.21. 把代数式通过配方等手段得到完全平方式,再运用完全平方式的非负性这一性质解决问题,这种解题方法叫做配方法.配方法在代数式求值,解方程,最值问题等都有广泛的应用.如利用配方法求最小值,求的最小值.解: , 因为不论a取何值,总是非负数,即 .
所以 , 所以当时,有最小值 .
根据上述材料,解答下列问题:
(1)、在横线上添上一个常数项使之成为完全平方式:;(2)、将变形为的形式,并求出的最小值;(3)、若代数式 , 试求N的最大值.22. 如图1所示,边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形. (1)、请你分别表示出这两个图形中阴影部分的面积: , ;(只需表示,不必化简);(2)、请问以上结果可以验证哪个乘法公式?;(3)、试利用这个公式计算:
(1)、请你分别表示出这两个图形中阴影部分的面积: , ;(只需表示,不必化简);(2)、请问以上结果可以验证哪个乘法公式?;(3)、试利用这个公式计算:①;
②;
③ .
23. 如图,长方形中, , , P为长方形上的动点,动点P从A出发,沿着运动到D点停止,速度为 , 设点P运动时间为x秒,的面积为 .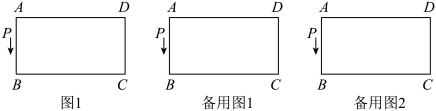 (1)、当时,对应y的值等于;时,对应y的值等于;(2)、当时,求y与x之间的关系式;(3)、当时,求对应x的值;(4)、当P在线段上运动时,是否存在点P使得的周长最小?若存在,求出此时的度数;若不存在,请说明理由.
(1)、当时,对应y的值等于;时,对应y的值等于;(2)、当时,求y与x之间的关系式;(3)、当时,求对应x的值;(4)、当P在线段上运动时,是否存在点P使得的周长最小?若存在,求出此时的度数;若不存在,请说明理由.
-
-