福建省福州市连江县2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-07-27 类型：期末考试

进入出卷网下载

一、选择题：本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 下列各组数中，能作为直角三角形三边长度的是（）

A、1，2，3 B、2，3，4 C、4，5，6 D、6，8，10

查看试题解析
2. 函数 $y = \sqrt{3 - x}$ 的自变量x的取值范围是（）

A、 $x < 3$ B、 $x \leq 3$ C、 $x > 3$ D、 $x \geq 3$

查看试题解析
3. 如图，在平行四边形ABCD中， $∠ A + ∠ C = 220 °$ ，则 $∠ B$ 的度数是（）

A、 $110 °$ B、 $90 °$ C、 $70 °$ D、 $50 °$

查看试题解析
4. 下列各图象中，表示y不是x的函数的是（）

A、 B、 C、 D、

查看试题解析
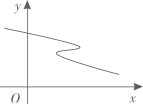5. 方程 $x^{2} - 4 x + 4 = 0$ 的根的情况是（）

A、有一个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、无实数根

查看试题解析
6. 用配方法解一元二次方程 $x^{2} + 8 x - 3 = 0$ ，配方后得到的方程是（）

A、 $(x - 4)^{2} = 19$ B、 $(x + 4)^{2} = 19$ C、 $(x - 4)^{2} = 13$ D、 $(x + 4)^{2} = 13$

查看试题解析
7. 如图是甲乙两位同学一个学期5次体能测试成绩折线统计图，下列说法正确的是（）

A、甲成绩比较稳定，且平均成绩较低 B、乙成绩比较稳定，且平均成绩较低 C、甲成绩比较稳定，且平均成绩较高 D、乙成绩比较稳定，且平均成绩较高

查看试题解析
8. 若直线 $y = k x + 2$ 与两条坐标轴围成的三角形的面积是2，则k的值为（）

A、1 B、 $- 1$ C、 $\pm 1$ D、 $\pm 2$

查看试题解析
9. 如图，某剧院舞台上的照明灯P射出的光线成“锥体”，其“锥体”面图的“锥角”是 $60 °$ ，已知舞台ABCD是边长为6的正方形，AC是正方形ABCD的对角线．要使灯光能照射到整个舞台，则灯P的悬挂高度是（）

A、 $3 \sqrt{6}$ B、 $3 \sqrt{3}$ C、 $4 \sqrt{3}$ D、 $\sqrt{6}$

查看试题解析
10. 已知正比例函数 $y = k x (k \neq 0)$ 的图象上任意两点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ，都有 $(x_{2} - x_{1}) (y_{2} - y_{1}) > 0$ ，那么一次函数 $y = k x - k$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题：本题共6小题，每小题4分，共24分．

11. 把直线 $y = - 4 x$ 向下平移3个单位长度后的直线表达式为．

查看试题解析

12. 为了了解某班同学一个月的课外阅读量，任选班上30名同学进行调查，统计如下表，则这些同学一个月的课外阅读量的众数是．

阅读量（单位：本/月）	0	1	2	3	4	5
人数（单位：人）	4	10	8	4	3	1

查看试题解析

13. 如图，在矩形ABCD中， $A B = 2 \sqrt{2}$ ，点E在边CD上， $△ A B E$ 的面积为 $3 \sqrt{6}$ ，则AD的长是．

查看试题解析
14. 如果m，n是方程 $x^{2} - 6 x + 4 = 0$ 的两个实数根，那么 $m + n - m n =$ ．

查看试题解析

15. 在物理实验课上，下表是小明记录了某根弹簧在弹性限度内所受拉力和弹簧长度的对应值，设所受拉力为

F (0 \leq F \leq 5 N)

，弹簧的长度为l，则l与F对应关系用解析式表示为．

弹力 $F / N$	0	0.5	1.0	1.5	2.0	2.5
弹簧的长度 $l / e m$	10	11.5	13	14.5	16	17.5

查看试题解析

16. 如图，在四边形ABCD中， $B C = 2 \sqrt{3}$ ， AD的垂直平分线分别交CD、BD、AD于点E、F、G，且 $E D = 5$ ， $B F = F D$ ， $A E / / B C$ ，则 $C E =$ ．

查看试题解析

三、解答题：本题共9小题，共86分．解答应写成文字说明、证明过程或演算步骤

17.

(1)、计算： $\sqrt{18} - \sqrt{\frac{1}{2}} + \sqrt{2} (\sqrt{2} + 1)$

(2)、解方程： $x^{2} - 2 x - 2 = 0$ ．

查看试题解析
18. 已知：如图，在ABCD中，点E在BC上，点F在BC的延长线上，且 $C F = B E$ ，连接AE，DF，求证： $A E = D F$ ．

查看试题解析
19. 一次函数 $y = k x + b (k \neq 0)$ 的图象经过 $A (- 1 ， 0)$ ， $B (0 ， - 3)$ 两点．

(1)、求出一次函数 $y = h k a x + b (k \neq 0)$ 的解析式；

(2)、在坐标系中画出此函数的图象，并求出线段AB的长．

查看试题解析
20. 如图，要在墙边围一个矩形花圃．花圃的一边靠墙（墙的长度为15米），另三边用篱笆围成．如果矩形花圃的面积为80平方米，篱笆长26米，求矩形花圃的长和宽各是多少米？

查看试题解析
21. 为进一步提高全民“节约用水”意识，某校组织学生进行家庭月用水量情况调查，小丽随机抽查了所住小区若干户家庭的月用水量，并根据调查结果绘制了下面两幅不完整的统计图．请根据统计图中信息，解答下列问题：

(1)、请补全条形统计图，被调查的家庭月用水量的中位数是 ▲ ；

(2)、求被调查的所有家庭的月平均用水量，并估计小丽所住小区400户家庭中月用水量低于月平均用水量的家庭户数．

查看试题解析
22. 福建连江有很多独特的美食，如鱼丸、肉燕等，某商场计划购进一批鱼丸和肉燕，已知一袋鱼丸的价格比一袋肉燕的价格多5元，且用250元钱购进鱼丸的袋数与用200元钱购进肉燕的袋数相等．

(1)、求鱼丸、肉燕每袋各多少元？

(2)、因连江鱼丸更受人欢迎，为了满足客户需求，若商店要购进两种商品鱼丸、肉燕共100袋，且鱼丸袋数不少于肉燕袋数的两倍，假设购买鱼丸为t袋，总费用为W元，怎样进货才能使所花的总费用W最少？并求出W的最小值．

查看试题解析
23. 如图，正方形ABCD中，连接AC，点E是BC延长线上一点，且 $C E < B C$ ，连接DE

(1)、尺规作图：在线段AC上求作一点F，使得 $D F = E F$ ；（保留作图痕迹，不写作法）

(2)、在（1）的条件下，连接DF，EF，试判断 $△ D E F$ 的形状，并说明理由．

查看试题解析
24. 在平面直角坐标系中，已知直线 $l_{1} ： y = 2 x + 4$ 分别与x轴，y轴交于A，B两点，直线 $l_{2} ： y_{2} = k x - 3 (k \neq 0)$

(1)、若直线 $l_{1}$ 与直线 $l_{2}$ 交于点 $P (a ， 2)$ ；
①求直线 $l_{2}$ 的函数解析式；
②当 $y_{1} > y_{2} > 0$ 时，请求出x的取值范围；

(2)、将线段AB沿某个方向平移得到线段EF，其中点 $F (m ， n)$ 是点B的对应点，点E是点A的对应点且在直线 $l_{2}$ 上，试说明n关于m的函数图象必经过一个定点，并求出该定点坐标．

查看试题解析
25. 如图1，矩形ABCD中，E为BC中点，连接AE， $B F ⊥ A E$ 于点G，交CD于F， $D H ⊥ A E$ 于点H， $G I / / C D$ ，交DH于点I．

(1)、求证： $G I = D F$ ；

(2)、若 $D F = F G$ ，求证：A、I、F三点共线；

(3)、如图2，连接HC交BF于点P，连接PI，求证：四边形GPIH是矩形．

查看试题解析