广东省广州市天河区2022-2023学年高二下学期期末数学试题

试卷更新日期：2023-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 在某项测试中，测量结果 $ξ$ 服从正态分布 $N (2 ， σ^{2})$ ，若 $P (2 < ξ < 4) = 0.2$ ，则 $P (ξ < 0) =$ （）

A、0.1 B、0.2 C、0.3 D、0.4

查看试题解析
2. 已知随机变量 $X ∼ B (4 ， \frac{2}{3})$ ，则 $P (X \geq 1)$ 的值为（）

A、 $\frac{80}{81}$ B、 $\frac{16}{81}$ C、 $\frac{65}{81}$ D、 $\frac{1}{81}$

查看试题解析
3. 已知数列 ${a_{n}}$ 满足 $a_{n + 1} - a_{n} = 3 (n \in N^{*})$ ， $a_{1} = - 6$ ，则 $| a_{1} | + | a_{2} | + | a_{3} | + | a_{4} | + | a_{5} | + | a_{6} | =$ （）

A、 $27$ B、 $18$ C、 $9$ D、 $0$

查看试题解析
4. 已知抛物线 $x = 2 y^{2}$ 上的点 $M$ 到其焦点的距离为 $2$ ，则点 $M$ 的横坐标是（）

A、 $\frac{3}{2}$ B、 $\frac{7}{4}$ C、 $\frac{15}{8}$ D、 $\frac{31}{16}$

查看试题解析
5. 古希腊时期，人们把宽与长之比为 $\frac{\sqrt{5} - 1}{2}$ 的矩形称为黄金矩形，把这个比值 $\frac{\sqrt{5} - 1}{2}$ 称为黄金分割比例，其中 $\frac{\sqrt{5} - 1}{2} \approx 0.618$ .如下图为希腊的一古建筑，其中图中的矩形 $A B C D$ 、 $B C F E$ 、 $C F G H$ 、 $F G J I$ 、 $G J K L$ 、 $J K M N$ 均为黄金矩形，若 $M$ 与 $K$ 之间的距离超过 $2 m$ ， $C$ 与 $F$ 之间的距离小于 $14.5 m$ ，则该古建筑中 $B$ 与 $C$ 之间的距离可能是（）
（参考数据： $0.61 8^{2} \approx 0.382$ ， $0.61 8^{3} \approx 0.236$ ， $0.61 8^{4} \approx 0.146$ ， $0.61 8^{5} \approx 0.090$ ， $0.61 8^{6} \approx 0.056$ ， $0.61 8^{7} \approx 0.034$ ）

A、 $22 m$ B、 $23 m$ C、 $24 m$ D、 $25 m$

查看试题解析
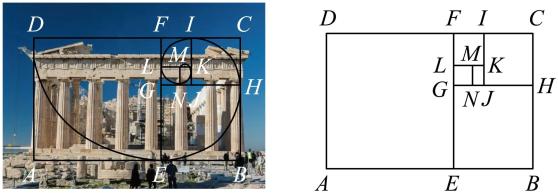6. 甲、乙、丙三人相互做传球训练，第 $1$ 次由甲将球传出，每次传球时，传球者都等可能地将球传给另外两个人中的任何一人，则 $4$ 次传球后球在乙手中的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{3}{8}$ D、 $\frac{5}{16}$

查看试题解析

7. 某校高二年级羽毛球社团为了解喜欢羽毛球运动是否与性别有关，随机在高二年级抽取了若干人进行调查.已知抽取的女生人数是男生人数的3倍，其中女生喜爱羽毛球运动的人数占女生人数的

\frac{2}{5}

，男生喜爱羽毛球运动的人数占男生人数的

\frac{3}{5}

.若本次调查得出“在犯错误的概率不超过0.05的前提下，认为喜爱羽毛球运动与性别有关”的结论，则被调查的男生至少有（）

参考公式及数据： $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ .

$α$	0.10	0.05	0.01	0.005	0.001
$x_{α}$	2.706	3.841	6.635	7.879	10.828

A、35人 B、32人 C、31人 D、30人

查看试题解析

8. 已知函数 $f (x) = a l n x + \frac{1}{2} x^{2}$ ，若对任意正数 $x_{1}$ ， $x_{2} (x_{1} \neq x_{2})$ ，都有 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} > 2$ 恒成立，则实数 $a$ 的取值范围为（）

A、 $(0 ， 1]$ B、 $(0 ， 2]$ C、 $[1 ， + \infty)$ D、 $[2 ， + \infty)$

查看试题解析

二、多选题

9. 已知 ${(2 - x)}^{8} = a_{0} + a_{1} x + a_{2} x^{2} + \cdot \cdot \cdot + a_{8} x^{8}$ ，则（）

A、 $a_{0} = 2^{8}$ B、 $a_{1} = 2^{10}$ C、 $a_{1} + a_{2} + \cdot \cdot \cdot + a_{8} = - 2^{8}$ D、展开式中所有项的二项式系数的和为 $2^{8}$

查看试题解析

10. 设离散型随机变量

X

的概率分布列如表，若

E (X) = 1

，

Y = 2 X + 1

，则下列各式正确的是（）

$X$	$- 1$	$0$	$6$
$P$	$\frac{1}{2}$	$a$	$b$

A、

P (X = 3) = \frac{1}{4}

B、

a = b = \frac{1}{4}

C、

E (Y) = 3

D、

D (Y) = 34

查看试题解析

11. 已知函数 $f (x) = e^{2 x} - 2 a x$ ， $a \in R$ ，则下列结论中正确的有（）

A、 $f (x)$ 必有唯一极值点 B、若 $a = 1$ ，则 $f (x)$ 在 $(- 1 ， 1)$ 上有极小值 $1$ C、若 $a = 1$ ，对 $\forall x \in [0 ， + ∞)$ 有 $f (x) \geq k x$ 恒成立，则 $k \leq 2 e - 2$ D、若存在 $x_{0} \in [2 ， 3]$ ，使得 $f (x_{0}) \leq 0$ 成立，则 $a \geq \frac{e^{6}}{6}$

查看试题解析
12. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1}$ 、 $F_{2}$ ，左、右顶点分别为 $A_{1}$ 、 $A_{2}$ ， $P$ 为双曲线右支上的一点，且直线 $P A_{1}$ 与 $P A_{2}$ 的斜率之积等于 $3$ ，则下列说法正确的是（）

A、双曲线 $C$ 的渐近线方程为 $y = \pm \sqrt{3} x$ B、若 $P F_{1} ⊥ P F_{2}$ ，且 $S_{△ P F_{1} F_{2}} = 6$ ，则 $a = 1$ C、分别以线段 $P F_{1}$ 、 $A_{1} A_{2}$ 为直径的两个圆内切 D、 $∠ P F_{2} A_{1} = 2 ∠ P A_{1} F_{2}$

查看试题解析

三、填空题

13. 椭圆 $\frac{y^{2}}{9} + \frac{x^{2}}{7} = 1$ 的离心率为.

查看试题解析
14. 有4名同学和2位老师排成一排合影，其中2位老师必须相邻，则不同的排法有种.（用数字作答）

查看试题解析

四、双空题

15. 要做一个无盖的长方体箱子，其体积为 $36 m^{3}$ ，底面长方形长与宽的比为 $2 ： 1$ ，则当它的宽为 $m$ 时，可使其表面积最小，最小表面积为 $m^{2}$ .

查看试题解析

五、填空题

16. 已知等比数列 ${a_{n}}$ 满足： $a_{1} + a_{2} = 20$ ， $a_{2} + a_{3} = 80$ .数列 ${b_{n}}$ 满足 $b_{n} = l o g_{2} a_{n} (n \in N^{*})$ ，其前 $n$ 项和为 $S_{n}$ ，若 $\frac{b_{n}}{S_{n} + 8} \leq λ$ 恒成立，则 $λ$ 的最小值为.

查看试题解析

六、解答题

17. 已知函数 $f (x) = x^{3} + a x^{2} + b x (a \in R ， b \in R)$ ，其图象在点 $(1 ， 4)$ 处的切线方程为 $y = 4$ .

(1)、求函数 $f (x)$ 的解析式；

(2)、求函数 $f (x)$ 在区间 $[\frac{1}{2} ， 4]$ 上的最值.

查看试题解析
18. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的焦点坐标为 $F_{1} (- 1 ， 0)$ 、 $F_{2} (1 ， 0)$ ，点 $A (1 ， \frac{\sqrt{2}}{2})$ 为椭圆 $C$ 上一点.

(1)、求椭圆 $C$ 的标准方程；

(2)、经过点 $F_{2}$ 且倾斜角为 $4 5^{∘}$ 的直线 $l$ 与椭圆 $C$ 相交于 $M$ 、 $N$ 两点， $O$ 为坐标原点，求 $△ O M N$ 的面积.

查看试题解析
19. $5$ 月 $25$ 日是全国大、中学生心理健康日，“ $5.25$ ”的谐音即为“我爱我”，意在提醒孩子们“珍惜生命、关爱自己”.学校将举行心理健康知识竞赛，第一轮选拔共设有 $A$ 、 $B$ 、 $C$ 三个问题，每位参加者按问题 $A$ 、 $B$ 、 $C$ 顺序作答，规则如下：
①每位参加者计分器的初始分均为 $10$ 分，答对问题 $A$ 、 $B$ 、 $C$ 分别加 $2$ 分、 $4$ 分、 $5$ 分，答错任一题减 $2$ 分；

②每回答一题，计分器显示累计分数，当累计分数小于 $8$ 分时，答题结束，淘汰出局；当累计分数大于或等于 $14$ 分时，答题结束，进入下一轮；

③当答完三题，若累计分数大于或等于 $14$ 分，则答题结束，进入下一轮；否则，答题结束，淘汰出局.

假设甲同学对问题 $A$ 、 $B$ 、 $C$ 回答正确的概率依次为 $\frac{3}{4}$ 、 $\frac{2}{3}$ 、 $\frac{1}{2}$ ，且各题回答正确与否相互之间没有影响.

(1)、求甲同学进入下一轮的概率；

(2)、用 $ξ$ 表示甲同学本轮答题结束时答对的个数，求 $ξ$ 的分布列和数学期望 $E (ξ)$ .

查看试题解析
20. 已知正项数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{n}^{2} + a_{n} = 2 S_{n} (n \in N^{*})$ ，数列 ${b_{n}}$ 是公比为2的等比数列，且 $b_{1} = a_{2}$ .

(1)、求数列 ${a_{n}}$ 和 ${b_{n}}$ 的通项公式；

(2)、数列 ${a_{n}}$ ， ${b_{n}}$ 的所有项按照“当 $n$ 为奇数时， $b_{n}$ 放在前面；当 $n$ 为偶数时， $a_{n}$ 放在前面”的要求进行“交叉排列”，得到一个新数列 ${c_{n}}$ ： $b_{1}$ ， $a_{1}$ ， $a_{2}$ ， $b_{2}$ ， $b_{3}$ ， $a_{3}$ ， $a_{4}$ ， $b_{4}$ ， …，求数列 ${c_{n}}$ 的前 $4 n + 3$ 项的和 $T_{4 n + 3}$ .

查看试题解析

21. 某医疗团队为研究

M

市的一种疾病发病情况与该市居民的年龄关系，从该市疾控中心得到以下数据：

年龄段（岁）	$[20 ， 30)$	$[30 ， 40)$	$[40 ， 50)$	$[50 ， 60)$	$[60 ， 70)$
发病率（ $‰$ ）	0.09	0.18	0.30	0.40	0.53

参考公式及数据： $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ ， $\sum_{i = 1}^{5} x_{i}^{2} = 11125$ ， $\sum_{i = 1}^{5} x_{i} y_{i} = 78.5$ .

(1)、若将每个区间的中点数据记为

x_{i}

，对应的发病率记为

y_{i}

（

i = 1

， 2，3，4，5），根据这些数据可以建立发病率

y (‰)

关于年龄

x

（岁）的经验回归方程

\hat{y} = \hat{b} x + \hat{a}

，求

\hat{a}

；

(2)、医学研究表明，化验结果有可能出现误差.现有

M

市某一居民年龄在

[40 ， 50)

，

A

表示事件“该居民化验结果呈阳性”，

B

表示事件“该居民患有这种疾病”.用频率估计概率，已知

P (A | B) = 0.9 ， P (\bar{A} | \bar{B}) = 0.8

，求

P (A)

查看试题解析

22. 已知函数 $f (x) = l n x + a x^{2}$ ， $a \in R$ .

(1)、讨论 $f (x)$ 的单调性；

(2)、当 $a = 1$ 时，证明： $f (x) \leq x^{2} + x - 1$ ；

(3)、证明：对任意的 $n \in N^{*}$ 且 $n \geq 2$ ，都有： $(1 + \frac{1}{2^{2}}) (1 + \frac{1}{3^{2}}) (1 + \frac{1}{4^{2}}) \cdot \cdot \cdot (1 + \frac{1}{n^{2}}) < \sqrt[3]{e^{2}}$ .

查看试题解析