上海市杨浦区2022-2023学年高二下学期期末数学试题
试卷更新日期:2023-07-27 类型:期末考试
一、填空题
-
1. 抛物线 的焦点坐标是 .2. 抛掷一颗质地均匀的正方体骰子,得点数的概率是.3. 半径为1厘米的球的表面积为平方厘米.4. 如图,正方体中,异面直线与所成角的大小是.
 5. 双曲线 的渐近线方程为.6. 以为圆心,且经过的圆的方程是.7. 如图所示,靶子由一个中心圆面Ⅰ和两个同心圆环Ⅱ、Ⅲ构成,射手命中Ⅰ、Ⅱ、Ⅲ的概率分别为0.35、0.30、0.25,则不命中靶的概率是.
5. 双曲线 的渐近线方程为.6. 以为圆心,且经过的圆的方程是.7. 如图所示,靶子由一个中心圆面Ⅰ和两个同心圆环Ⅱ、Ⅲ构成,射手命中Ⅰ、Ⅱ、Ⅲ的概率分别为0.35、0.30、0.25,则不命中靶的概率是. 8. “若直线平面 , 直线在平面上,则直线直线”是命题(填“真”或“假”).9. 已知一个圆锥的体积为 , 高为3,则该圆锥的母线与底面所成角的大小是.10. 已知与是独立事件, , 给出下列式子:①;②;③;④;
8. “若直线平面 , 直线在平面上,则直线直线”是命题(填“真”或“假”).9. 已知一个圆锥的体积为 , 高为3,则该圆锥的母线与底面所成角的大小是.10. 已知与是独立事件, , 给出下列式子:①;②;③;④;其中正确的式子是.(填序号)
11. 如图,正三棱柱的各条棱长都相等,线段、和是该正三棱柱的三条面对角线,直线与这三条面对角线所在直线所成的角大小相同,则这个角的大小是(写出所有可能的值).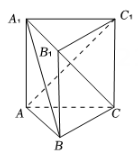 12. 已知数列 , , , ...,的各项均为正整数,其中 , 对于每个正整数 , 为相同的正整数,则的值是.
12. 已知数列 , , , ...,的各项均为正整数,其中 , 对于每个正整数 , 为相同的正整数,则的值是.二、单选题
-
13. 在长方体中,与相等的向量是( )A、 B、 C、 D、14. 如图,已知球的半径为5,球心到平面的距离为3,则平面截球所得的小圆的半径长是( )
 A、2 B、3 C、 D、415. 下列命题:
A、2 B、3 C、 D、415. 下列命题:①底面是正多边形的棱锥是正棱锥;②各侧棱的长都相等的棱锥是正棱锥;③各侧面是全等的等腰三角形的棱锥是正棱锥.
其中真命题的个数是( )
A、0 B、1 C、2 D、316. 小李购买了一盒点心,点心盒是长方体,长、宽、高分别为30厘米、20厘米和10厘米,商家提供丝带捆扎服务,有如图所示两种捆扎方案(粗线表示丝带)可供选择,免去手工费,但丝带需要按使用长度进行收费.假设丝带紧贴点心盒表面,且不计算丝带宽度以及重叠粘合打结的部分.为了节约成本,小李打算选择尽可能使用丝带较短的方案,则小李需要购买的丝带长度至少是( ) A、80厘米 B、100厘米 C、120厘米 D、140厘米
A、80厘米 B、100厘米 C、120厘米 D、140厘米三、解答题
-
17. 设等比数列的前项和为 , 已知 , .(1)、求公比的值;(2)、求的值.18. 已知 , 直线 , 直线.(1)、若 , 求与之间的距离;(2)、若与的夹角大小为 , 求直线的方程.19. 某校高二年级共有学生200人,其中男生120人,女生80人.为了了解全年级学生上学花费时间(分)的信息,按照分层抽样的原则抽取了样本,样本容量为20,并根据样本数据信息绘制了茎叶图和频率分布直方图.由于保存不当,茎叶图中有一个数据不小心被污染看不清了(如图),频率分布直方图纵轴上的数据也遗失了.
 (1)、根据茎叶图提供的有限信息,求频率分布直方图中和的值,指出样本的“中位数、平均数、众数、方差、极差”中,哪些已经能确定,并计算它们的值;(2)、通过对样本原始数据的计算,得到男生上学花费时间的样本均值为30(分),女生的样本均值为27.75(分),试计算被污染的数值,并根据样本估计该年级全体学生上学花费时间的“中位数、平均数、方差”.
(1)、根据茎叶图提供的有限信息,求频率分布直方图中和的值,指出样本的“中位数、平均数、众数、方差、极差”中,哪些已经能确定,并计算它们的值;(2)、通过对样本原始数据的计算,得到男生上学花费时间的样本均值为30(分),女生的样本均值为27.75(分),试计算被污染的数值,并根据样本估计该年级全体学生上学花费时间的“中位数、平均数、方差”.

