广东省广州市白云区2022-2023学年高一下学期期末数学试题

试卷更新日期：2023-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 已知向量 $\vec{a} = (3 ， - 6)$ ， $\vec{b} = (2 ， λ) (λ \in R)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则 $λ =$ （）

A、－4 B、－1 C、1 D、4

查看试题解析
2. 抛掷两枚质地均匀的骰子，则“抛掷的两枚骰子的点数之和是6”的概率为（）

A、 $\frac{1}{12}$ B、 $\frac{5}{36}$ C、 $\frac{1}{7}$ D、 $\frac{1}{6}$

查看试题解析
3. 已知甲组样本数据分别为4，6，9，11，x，且平均数为7，若乙组样本数据为7，11，17，21， $2 x - 1$ ，则乙组样本数据的平均数为（）

A、13 B、14 C、27 D、28

查看试题解析
4. 已知 $2 - i$ 是关于x的方程 $x^{2} + p x + q = 0$ 的一个根，则实数p，q分别为（）

A、 $p = 4 ， q = - 11$ B、 $p = - 4 ， q = 3$ C、 $p = 4 ， q = - 3$ D、 $p = - 4 ， q = 5$

查看试题解析
5. 已知等腰直角三角形的斜边长为 $\sqrt{2}$ ，以直角边所在直线为轴，其余两边旋转一周形成的面围成一个几何体，这个几何体的表面积为（）

A、 $\frac{π}{3}$ B、 $2 π$ C、 $(\sqrt{2} + 1) π$ D、 $(2 \sqrt{2} + 1) π$

查看试题解析
6. 四名同学各掷骰子5次，分别记录每次骰子出现的点数.根据四名同学的统计结果，可以判断出一定没有出现点数6的是（）

A、中位数为3，众数为3 B、中位数为3，极差为3 C、平均数为3，中位数为3 D、平均数为3，众数为4

查看试题解析
7. 已知棱长为1的正方体的顶点都在同一球面上.先从正方体的8个顶点中任取4个共面的点，再从球面上取1个点，形成四棱锥，这些四棱锥的体积的最大值为（）

A、 $\frac{1 + \sqrt{3}}{6}$ B、 $\frac{\sqrt{6}}{6}$ C、 $\frac{\sqrt{3}}{4}$ D、 $\frac{2 + \sqrt{3}}{12}$

查看试题解析
8. 已知点P在 $△ A B C$ 所在平面内，满足 $\vec{P A} + \vec{P B} + \vec{P C} = \vec{0}$ ，且 $\vec{A B} = m \vec{A P} + n \vec{A C}$ ，则 $m + n =$ （）

A、 $\frac{2}{3}$ B、1 C、 $\frac{4}{3}$ D、2

查看试题解析

二、多选题

9. 若平面 $α ⊥$ 平面 $β$ ，且 $α ∩ β = l$ ，则下列命题中正确的是（）

A、交线l的垂线必垂直于平面 $β$ B、与平面 $α$ 垂直的直线平行于平面 $β$ 或在平面 $β$ 内 C、平面 $α$ 内的任一条直线必垂直于平面 $β$ 内无数条直线 D、过平面 $α$ 内任意一点作交线l的垂线，则此垂线必垂直于平面 $β$

查看试题解析
10. 已知A，B是一个随机试验中的两个随机事件，若 $P (A B) = \frac{2}{9}$ ， $P (A) = \frac{2}{3}$ ， $P (B) = \frac{1}{3}$ ，则（）

A、事件A与B互为对立 B、事件A与B相互独立 C、 $P (A ∪ B) = \frac{7}{9}$ D、 $P (\bar{A B}) = \frac{2}{9}$

查看试题解析
11. 设 $z_{1}$ ， $z_{2}$ ， $z_{3}$ 为复数，且 $z_{1} \neq z_{2}$ .下列命题中正确的是（）

A、若 $z_{1} z_{3} = z_{2} z_{3}$ ，则 $z_{3} = 0$ B、若 $z_{1} = z_{3}$ ，则 ${| z_{1} |}^{2} = z_{1} z_{3}$ C、若 $| z_{1} - z_{2} | = | z_{1} + z_{2} |$ ，则 $z_{1} z_{2} = 0$ D、若 ${\bar{z}}_{2} = z_{3}$ ，则 $| z_{1} z_{2} | = | z_{1} z_{3} |$

查看试题解析
12. 在 $△ A B C$ 中，三个角A，B，C所对的边分别为a，b，c， $\vec{A D} = λ \vec{A C} (λ \in R)$ ，记 $∠ A B D = θ$ .下列命题中正确的是（）

A、若 $λ = \frac{1}{2}$ ，则 $c s i n θ = a s i n (B - θ)$ B、若 $λ = \frac{1}{2}$ ，则 $c c o s θ + b c o s (A + θ) = B D$ C、若 $λ \in [0 ， 1]$ ，则 $\frac{s i n θ}{a} + \frac{s i n (B - θ)}{c} = \frac{s i n B}{B D}$ D、若 $λ \in [0 ， 1]$ ，则 $a c o s (B - θ) + b c o s (A + θ) = c c o s θ$

查看试题解析

三、填空题

13. 某市2023年6月某一周的空气质量指数如下：
35 54 80 86 72 85 58

这一周空气质量指数的第60百分位数为.

查看试题解析
14. 已知复数 $z = \frac{1 - i}{1 + i}$ ， i为虚数单位，则z的虚部为.

查看试题解析

四、双空题

15. 在 $△ A B C$ 中，已知 $A B = 2$ ， $A C = 6 \sqrt{2}$ ， $∠ B A C = 45 °$ ，点D为边 $B C$ 的中点，则 $A D =$ ， $s i n ∠ B A D =$ .

查看试题解析

五、填空题

16. 在棱长为a的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，E，F分别为棱BC， $C C_{1}$ 的中点，过点A，E，F作一个截面，该截面将正方体分成两个多面体，则体积较小的多面体的体积为.

查看试题解析

六、解答题

17. 已知 $△ A B C$ 的内角A，B，C所对的边分别为a，b，c，向量 $\vec{m} = (s i n A ， \sqrt{3} c o s A)$ ， $\vec{n} = (1 ， 1)$ ，且 $\vec{m} ∥ \vec{n}$ .

(1)、求角A；

(2)、若 $a = 2 \sqrt{7}$ ， b＝4，求 $△ A B C$ 的周长.

查看试题解析
18. 图1是正方形 $A B C D$ ， E，F，G分别是 $A B$ ， $B C$ ， $C D$ 的中点.将其沿对角线AC折起，连结DB，如图2.请在图2中证明：

(1)、 $A C / /$ 平面EFG；

(2)、 $A C ⊥ D B$ .

查看试题解析
19. 为了解某市今年高一年级学生的身体素质状况，从该市高一年级学生中抽取100名学生进行“掷实心球”的项目测试.经统计，成绩均在2米到12米之间，把获得的所有数据分 $[2 ， 4)$ ， $[4 ， 6)$ ， $[6 ， 8)$ ， $[8 ， 10)$ ， $[10 ， 12)$ 成五组，得到频率分布直方图如图所示.

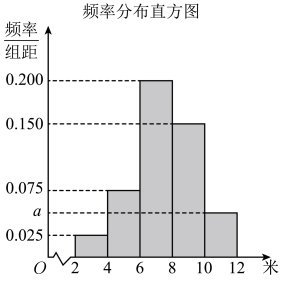(1)、根据频率分布直方图，估计该市今年高一年级学生“掷实心球”成绩的平均数（同一组中的数据以该组区间的中点值作代表）；

(2)、已知这100名学生中有女生40名，男生60名，这40名女生“掷实心球”成绩的平均数和方差分别为7和2.1，这60名男生“掷实心球”成绩的平均数和方差分别为8.5和2.4，求这100名学生“掷实心球”成绩的方差.

查看试题解析
20. 甲、乙两人参加猜成语活动，每轮活动由甲、乙各猜一个成语，已知甲每轮猜对的概率为 $\frac{2}{3}$ ，乙每轮猜对的概率为 $\frac{1}{2}$ .在每轮活动中，甲和乙猜对与否互不影响，各轮结果也互不影响.

(1)、求经过两轮活动，两人共猜对2个成语的概率；

(2)、求经过两轮活动，两人猜对成语的个数不相同的概率.

查看试题解析
21. 如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，平面 $A_{1} B C ⊥$ 平面 $A B B_{1} A_{1}$ ，

(1)、求证： $B C ⊥$ 平面 $A B B_{1} A_{1}$ ；

(2)、若直线 $A C$ 与平面 $A_{1} B C$ 所成角为 $α$ ，二面角 $A_{1} - B C - A$ 的大小为 $β$ ，试判断 $α$ ， $β$ 的大小关系，并予以证明.

查看试题解析
22. 古希腊的数学家海伦在其著作《测地术》中给出了由三角形的三边长a，b，c计算三角形面积的公式： $S = \sqrt{p (p - a) (p - b) (p - c)}$ ，这个公式常称为海伦公式.其中， $p = \frac{1}{2} (a + b + c)$ .我国南宋著名数学家秦九韶在《数书九章》中给出了由三角形的三边长a，b，c计算三角形面积的公式： $S = \sqrt{\frac{1}{4} [c^{2} a^{2} - {(\frac{c^{2} + a^{2} - b^{2}}{2})}^{2}]}$ ，这个公式常称为“三斜求积”公式.

(1)、利用以上信息，证明三角形的面积公式 $S = \frac{1}{2} a c s i n B$ ；

(2)、在 $△ A B C$ 中， $a + c = 8$ ， $t a n \frac{B}{2} = \frac{s i n A}{2 - c o s A}$ ，求 $△ A B C$ 面积的最大值.

查看试题解析