浙江省温州市十校联合体2022-2023学年高二下学期期末联考数学试题
试卷更新日期:2023-07-27 类型:期末考试
一、单选题
-
1. 集合 , 集合 , 则( )A、 B、 C、 D、2. 复数的实部与虚部互为相反数,且满足 , , 则复数在复平面上对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 函数的大致图象为A、
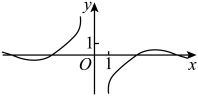 B、
B、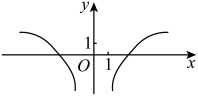 C、
C、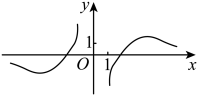 D、
D、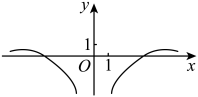 4. 的展开式中各项系数的和为 , 则该展开式中常数项为( )A、 B、 C、20 D、405. 冯老师教高二4班和5班两个班的数学,这两个班的人数相等.某次联考中,这两个班的数学成绩均近似服从正态分布,其正态密度函数的图像如图所示,其中是正态分布的期望,是正态分布的标准差,且 , , .关于这次数学考试成绩,下列结论正确的是( )
4. 的展开式中各项系数的和为 , 则该展开式中常数项为( )A、 B、 C、20 D、405. 冯老师教高二4班和5班两个班的数学,这两个班的人数相等.某次联考中,这两个班的数学成绩均近似服从正态分布,其正态密度函数的图像如图所示,其中是正态分布的期望,是正态分布的标准差,且 , , .关于这次数学考试成绩,下列结论正确的是( ) A、4班的平均分比5班的平均分高 B、相对于5班,4班学生的数学成绩更分散 C、4班108分以上的人数约占该班总人数的4.55% D、5班112分以上的人数与4班108分以上的人数大致相等6. 冬季两项是冬奥会的项目之一,是把越野滑雪和射击两种不同特点的竞赛项目结合在一起进行的运动,其中冬季两项男子个人赛,选手需要携带枪支和20发子弹,每滑行4千米射击一轮,共射击4轮,每轮射击5次,若每有1发子弹没命中,则被罚时1分钟,总用时最少者获胜.已知某男选手在一次比赛中共被罚时3分钟,假设其射击时每发子弹命中的概率都相同,且每发子弹是否命中相互独立,记事件为其在前两轮射击中没有被罚时,事件为其在第4轮射击中被罚时2分钟,那么( )A、 B、 C、 D、7. 我们知道:的图象关于原点成中心对称图形的充要条件是为奇函数,有同学发现可以将其推广为:的图象关于成中心对称图形的充要条件是为奇函数.若的对称中心为 , 则( )A、8088 B、4044 C、 D、8. 设 , , , 则下列关系正确的是( )A、 B、 C、 D、
A、4班的平均分比5班的平均分高 B、相对于5班,4班学生的数学成绩更分散 C、4班108分以上的人数约占该班总人数的4.55% D、5班112分以上的人数与4班108分以上的人数大致相等6. 冬季两项是冬奥会的项目之一,是把越野滑雪和射击两种不同特点的竞赛项目结合在一起进行的运动,其中冬季两项男子个人赛,选手需要携带枪支和20发子弹,每滑行4千米射击一轮,共射击4轮,每轮射击5次,若每有1发子弹没命中,则被罚时1分钟,总用时最少者获胜.已知某男选手在一次比赛中共被罚时3分钟,假设其射击时每发子弹命中的概率都相同,且每发子弹是否命中相互独立,记事件为其在前两轮射击中没有被罚时,事件为其在第4轮射击中被罚时2分钟,那么( )A、 B、 C、 D、7. 我们知道:的图象关于原点成中心对称图形的充要条件是为奇函数,有同学发现可以将其推广为:的图象关于成中心对称图形的充要条件是为奇函数.若的对称中心为 , 则( )A、8088 B、4044 C、 D、8. 设 , , , 则下列关系正确的是( )A、 B、 C、 D、二、多选题
-
9. 已知数列的前项和为 , 且 , , 则下列命题正确的是( )A、 B、 C、 D、10. 已知圆 , 点 , 点在圆上,为原点,则下列命题正确的是( )A、在圆上 B、线段长度的最大值为 C、当直线与圆相切时, D、的最大值为11. 已知 , , 为实数,则满足函数有且仅有一个零点的条件是( )A、 , B、 , C、 , D、 ,12. 已知三棱锥 , , 其余棱长均为 , 则下列命题正确的是( )A、该几何体外接球的表面积为 B、直线和所成的角的余弦值是 C、若点在线段上,则最小值为3 D、到平面的距离是
三、填空题
-
13. 已知平面向量 , , , , , 则的值是.14. 如图所示,为平面四边形的对角线,设 , , 为等边三角形,则四边形的面积的最大值为.
 15. 已知椭圆的左顶点为 , 上顶点为 , 为坐标原点,椭圆上的两点 , 分别在第一,第二象限内,若与的面积相等,且 , 则椭圆的离心率为.16. 函数为数学家高斯创造的取整函数,表示不超过的最大整数,如 , , 已知数列满足 , 且 , 若 , 则数列的前2023项和为.
15. 已知椭圆的左顶点为 , 上顶点为 , 为坐标原点,椭圆上的两点 , 分别在第一,第二象限内,若与的面积相等,且 , 则椭圆的离心率为.16. 函数为数学家高斯创造的取整函数,表示不超过的最大整数,如 , , 已知数列满足 , 且 , 若 , 则数列的前2023项和为.四、解答题
-
17. 如图所示,在棱长为1的正方体中为线段的中点.
 (1)、求证:平面平面;(2)、求到平面的距离.18. 设公差不为零的等差数列 , , , , 成等比数列.(1)、求数列的通项公式;(2)、已知 , 数列的前项和为 , 求使得成立的最小正整数.19. 中,三个内角 , , 所对的边分别为 , , 且(1)、若 , , 求内切圆的半径长;(2)、已知 , , 求的面积.20. 三门是“中国青蟹之乡”,气候温暖、港湾平静、水质优良,以优越的自然环境成为我国优质青蟹的最佳产区.所产的三门青蟹具有“金爪、绯钳、青背、黄肚”的特征,以“壳薄、皆黄、肉嫩、味美”而著称,素有“三门青蟹、横行世界”之美誉;且营养丰富,内含人体所需的18种氨基酸和蛋白质、脂肪、钙、磷、铁等营养成分,被誉为“海中黄金,蟹中臻品”.养殖户一般把重量超过350克的青蟹标记为类青蟹(1)、现有一个小型养蟹池,已知蟹池中有50只青蟹,其中类青蟹有7只,若从池中抓了2只青蟹,用表示其中类青蟹的只数,请写出的分布列,并求的数学期望;(2)、另有一个养蟹池,为估计蟹池中的青蟹数目 , 小王先从中抓了50只青蟹,做好记号后放回池中,过了一段时间后,再从中抓了20只青蟹,发现有记号的有只,若 , 试给出蟹池中青蟹数目的估计值(以使取得最大值的为估计值).
(1)、求证:平面平面;(2)、求到平面的距离.18. 设公差不为零的等差数列 , , , , 成等比数列.(1)、求数列的通项公式;(2)、已知 , 数列的前项和为 , 求使得成立的最小正整数.19. 中,三个内角 , , 所对的边分别为 , , 且(1)、若 , , 求内切圆的半径长;(2)、已知 , , 求的面积.20. 三门是“中国青蟹之乡”,气候温暖、港湾平静、水质优良,以优越的自然环境成为我国优质青蟹的最佳产区.所产的三门青蟹具有“金爪、绯钳、青背、黄肚”的特征,以“壳薄、皆黄、肉嫩、味美”而著称,素有“三门青蟹、横行世界”之美誉;且营养丰富,内含人体所需的18种氨基酸和蛋白质、脂肪、钙、磷、铁等营养成分,被誉为“海中黄金,蟹中臻品”.养殖户一般把重量超过350克的青蟹标记为类青蟹(1)、现有一个小型养蟹池,已知蟹池中有50只青蟹,其中类青蟹有7只,若从池中抓了2只青蟹,用表示其中类青蟹的只数,请写出的分布列,并求的数学期望;(2)、另有一个养蟹池,为估计蟹池中的青蟹数目 , 小王先从中抓了50只青蟹,做好记号后放回池中,过了一段时间后,再从中抓了20只青蟹,发现有记号的有只,若 , 试给出蟹池中青蟹数目的估计值(以使取得最大值的为估计值).