安徽省马鞍山市2022-2023学年高一下学期期末教学质量监测数学试题
试卷更新日期:2023-07-27 类型:期末考试
一、单选题
-
1. 复数(其中为虚数单位)的虚部为( )A、1 B、-1 C、 D、2. ( )A、 B、 C、 D、3. 下列各组向量中,可以作为基底的是( )A、 , B、 , C、 , D、 ,4. 通过抽样调查得到某栋居民楼12户居民的月均用水量数量(单位:吨),如下表格:
4.1
3.2
4.2
5.6
4.3
5.0
6.3
6.2
3.5
3.9
4.5
5.2
则这12户居民的月均用水量的第75百分位数为( )
A、5.0 B、5.2 C、5.4 D、5.65. 已知是空间两个不同的平面,是空间两条不同的直线,则下列命题为真命题的是( )A、若 , 则 B、若 , 则 C、若 , 且 , 则 D、若 , 且 , 则6. 将函数的图象上各点的横坐标伸长到原来的倍(纵坐标不变),得到函数的图象,则( )A、 B、 C、 D、7. 正方形ABCD中,E,F分别是边AD,DC的中点,BE与AF交于点G.则( )A、 B、 C、 D、8. 在直三棱柱中, , , , 且三棱柱的所有顶点都在同一球面上,则该球的表面积为( )A、 B、 C、 D、二、多选题
-
9. 若复数z满足(为虚数单位),则( )A、 B、 C、 D、10. 已知函数的部分图象,则( )
 A、 B、 C、点是图象的一个对称中心 D、的图象向左平移个单位后所对应的函数为偶函数11. 在中,下列说法正确的是( )A、若 , 则 B、若 , 则为锐角三角形 C、若 , 则为钝角三角形 D、存在满足12. 在正方体中,E,F分别为AB,BC的中点,G为线段上的动点,过E,F,G作正方体的截面记为 , 则( )
A、 B、 C、点是图象的一个对称中心 D、的图象向左平移个单位后所对应的函数为偶函数11. 在中,下列说法正确的是( )A、若 , 则 B、若 , 则为锐角三角形 C、若 , 则为钝角三角形 D、存在满足12. 在正方体中,E,F分别为AB,BC的中点,G为线段上的动点,过E,F,G作正方体的截面记为 , 则( )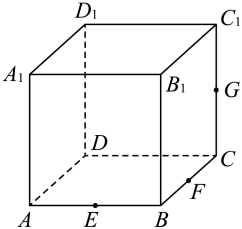 A、当截面为正六边形时,G为中点 B、当时,截面为五边形 C、截面可能是等腰梯形 D、截面不可能与直线垂直
A、当截面为正六边形时,G为中点 B、当时,截面为五边形 C、截面可能是等腰梯形 D、截面不可能与直线垂直三、填空题
-
13. 已知向量 , , 且 , 则.14. 已知某圆锥的侧面积为 , 其侧面展开图是半圆,则该圆锥的体积为 .15. 计算: .16. 已知△ABC是钝角三角形,角A,B,C的对边依次是a,b,c,且 , , 则边c的取值范围是 .
四、解答题
-
17. 某小学对在校学生开展防震减灾教育,进行一段时间的展板学习和网络学习后,学校对全校学生进行问卷测试(满分分).现随机抽取了部分学生的答卷,得分的频数统计表和对应的频率分布直方图如图所示:

得分
人数
(1)、求 , 的值,并估计全校学生得分的平均数;(2)、根据频率分布直方图,估计样本数据的和分位数.18. 在中,角A,B,C的对边依次是a,b,c.若.(1)、求角C;(2)、当 , 时,求的面积.19. 如图所示,在直三棱柱中, , D,E分别为棱AB,的中点. (1)、证明:CD∥平面;(2)、求BE与平面所成角的正弦值.
(1)、证明:CD∥平面;(2)、求BE与平面所成角的正弦值.
