北师大版数学九年级上册同步练习——第四章《图形的相似》综合练习(A)
试卷更新日期:2023-07-27 类型:单元试卷
一、选择题(每题3分,共36分)
-
1. 若 , 则( )A、6 B、 C、1 D、2. 若两个相似三角形周长的比为 , 则这两个三角形对应边的比是( )A、 B、 C、 D、3. 如图,将三角尺直立举起靠近墙面,打开手机手电筒照射三角尺,在墙面上形成影子.则三角尺与影子之间属于以下哪种图形变换( )
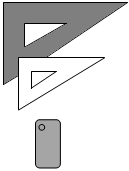 A、平移 B、轴对称 C、旋转 D、位似4. 如图,已知 , , 若的长度为6,则的长度为( )
A、平移 B、轴对称 C、旋转 D、位似4. 如图,已知 , , 若的长度为6,则的长度为( )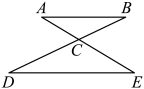 A、4 B、9 C、12 D、5. 已知 , ,若 ,则 ( )A、4 B、6 C、8 D、166. 已知△ABC与△A1B1C1是位似图形,位似比是1:3,则△ABC与△A1B1C1的面积比( )A、1 :3 B、1:6 C、1:9 D、3:17. 如图,在△ABC中,DE∥AB,且 = ,则 的值为( )
A、4 B、9 C、12 D、5. 已知 , ,若 ,则 ( )A、4 B、6 C、8 D、166. 已知△ABC与△A1B1C1是位似图形,位似比是1:3,则△ABC与△A1B1C1的面积比( )A、1 :3 B、1:6 C、1:9 D、3:17. 如图,在△ABC中,DE∥AB,且 = ,则 的值为( ) A、 B、 C、 D、8. 如图所示,某校数学兴趣小组利用标杆 测量建筑物的高度,已知标杆 高 ,测得 , ,则建筑物 的高是( )
A、 B、 C、 D、8. 如图所示,某校数学兴趣小组利用标杆 测量建筑物的高度,已知标杆 高 ,测得 , ,则建筑物 的高是( )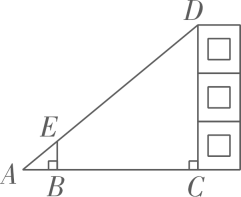 A、 B、 C、 D、9. 如图,为等边三角形,点 , 分别在边 , 上, , 若 , , 则的长为( )
A、 B、 C、 D、9. 如图,为等边三角形,点 , 分别在边 , 上, , 若 , , 则的长为( ) A、 B、 C、 D、10. 如图,在中, , 点在边上,且平分的周长,则的长是( )
A、 B、 C、 D、10. 如图,在中, , 点在边上,且平分的周长,则的长是( )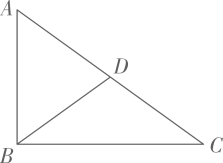 A、 B、 C、 D、11. 如图,是的中位线,点在上,连接并延长,与的延长线相交于点若 , 则线段的长为( )
A、 B、 C、 D、11. 如图,是的中位线,点在上,连接并延长,与的延长线相交于点若 , 则线段的长为( ) A、 B、 C、 D、12. 如图,四边形是一张矩形纸片.将其按如图所示的方式折叠:使边落在边上,点落在点处,折痕为;使边落在边上,点落在点处,折痕为 . 若矩形与原矩形相似, , 则的长为( )
A、 B、 C、 D、12. 如图,四边形是一张矩形纸片.将其按如图所示的方式折叠:使边落在边上,点落在点处,折痕为;使边落在边上,点落在点处,折痕为 . 若矩形与原矩形相似, , 则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
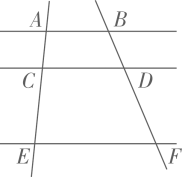
13. 如图, .若 , ,则 .
 14. 如图,在平面直角坐标系中,四边形的顶点坐标分别是 , 若四边形与四边形关于原点位似,且四边形的面积是四边形面积的4倍,则第一象限内点的坐标为 .
14. 如图,在平面直角坐标系中,四边形的顶点坐标分别是 , 若四边形与四边形关于原点位似,且四边形的面积是四边形面积的4倍,则第一象限内点的坐标为 . 15. 如图,和是以点为位似中心的位似图形,点在线段上.若 , 则和的周长之比为 .
15. 如图,和是以点为位似中心的位似图形,点在线段上.若 , 则和的周长之比为 .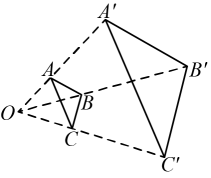 16. 如图,在Rt中, , 将绕点逆时针方向旋转 , 得到.连接 , 交AC于点 , 则的值为.
16. 如图,在Rt中, , 将绕点逆时针方向旋转 , 得到.连接 , 交AC于点 , 则的值为.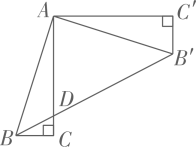 17. 如图,在四边形中, , 对角线相交于点 . 若 , 则的长为 .
17. 如图,在四边形中, , 对角线相交于点 . 若 , 则的长为 .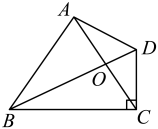 18. 如图,平分等边的面积,折叠得到分别与相交于两点.若 , 用含的式子表示的长是 .
18. 如图,平分等边的面积,折叠得到分别与相交于两点.若 , 用含的式子表示的长是 .
三、解答题(共7题,共66分)
-
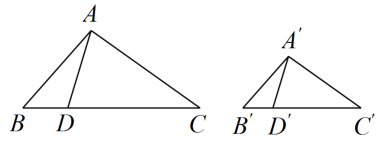
19. 如图,在与中,点、分别在边、上,且 , 若 ▲ , 则 . 请从①;②;③这三个选项中选择一个作为条件(写序号),并加以证明.
 20. 如图,在中, , E是边AC上一点,且 , 过点A作BE的垂线,交BE的延长线于点D,求证: .
20. 如图,在中, , E是边AC上一点,且 , 过点A作BE的垂线,交BE的延长线于点D,求证: .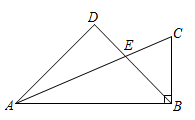 21. 如图,△ABC是一块锐角三角形的材料,边BC=120mm , 高AD=80mm , 要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少mm .
21. 如图,△ABC是一块锐角三角形的材料,边BC=120mm , 高AD=80mm , 要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少mm .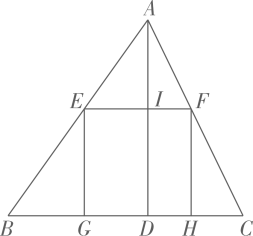 22. 如图,将边长为3的正方形沿直线折叠,使点的对应点落在边上(点不与点重合),点落在点处,与交于点 , 折痕分别与边 , 交于点 , 连接 .
22. 如图,将边长为3的正方形沿直线折叠,使点的对应点落在边上(点不与点重合),点落在点处,与交于点 , 折痕分别与边 , 交于点 , 连接 . (1)、求证:;(2)、若 , 求的长.23. 如图, , 点是线段上的一点,且 . 已知 .
(1)、求证:;(2)、若 , 求的长.23. 如图, , 点是线段上的一点,且 . 已知 .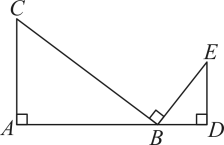 (1)、证明: .(2)、求线段的长.24. △ABC在边长为l的正方形网格中如图所示.
(1)、证明: .(2)、求线段的长.24. △ABC在边长为l的正方形网格中如图所示.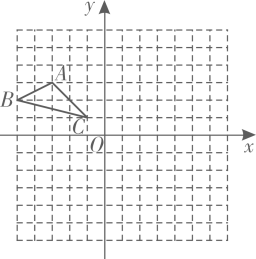
①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2.且△A1B1C位于点C的异侧,并表示出A1的坐标.
②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
③在②的条件下求出点B经过的路径长.
25. 如图,用四根木条钉成矩形框 ,把边 固定在地面上,向右推动矩形框,矩形框的形状会发生改变(四边形具有不稳定性).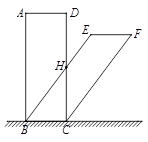 (1)、通过观察分析,我们发现图中线段存在等量关系,如线段 由 旋转得到,所以 .我们还可以得到 = , = ;(2)、进一步观察,我们还会发现 ∥ ,请证明这一结论;(3)、已知 ,若 恰好经过原矩形 边的中点 ,求 与 之间的距离.
(1)、通过观察分析,我们发现图中线段存在等量关系,如线段 由 旋转得到,所以 .我们还可以得到 = , = ;(2)、进一步观察,我们还会发现 ∥ ,请证明这一结论;(3)、已知 ,若 恰好经过原矩形 边的中点 ,求 与 之间的距离.