2023年高考真题分类汇编:牛顿定律、万有引力

试卷更新日期：2023-07-27 类型：二轮复习

进入出卷网下载

一、选择题

1. 2022年10月9日，我国综合性太阳探测卫星“夸父一号”成功发射，实现了对太阳探测的跨越式突破。“夸父一号”卫星绕地球做匀速圆周运动，距地面高度约为 $720km$ ，运行一圈所用时间约为100分钟。如图所示，为了随时跟踪和观测太阳的活动，“夸父一号”在随地球绕太阳公转的过程中，需要其轨道平面始终与太阳保持固定的取向，使太阳光能照射到“夸父一号”，下列说法正确的是（　　）

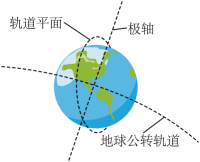A、 “夸父一号”的运行轨道平面平均每天转动的角度约为 $1 °$ B、“夸父一号”绕地球做圆周运动的速度大于 $7 .9km/s$ C、“夸父一号”绕地球做圆周运动的向心加速度大于地球表面的重力加速度 D、由题干信息，根据开普勒第三定律，可求出日地间平均距离

查看试题解析
2. 如图所示，在光滑水平地面上，两相同物块用细线相连，两物块质量均为1kg，细线能承受的最大拉力为2N。若在水平拉力F作用下，两物块一起向右做匀加速直线运动。则F的最大值为（）

A、1N B、2N C、4N D、5N

查看试题解析
3. 牛顿认为物体落地是由于地球对物体的吸引，这种吸引力可能与天体间（如地球与月球）的引力具有相同的性质、且都满足 $F \propto \frac{M m}{r^{2}}$ 。已知地月之间的距离r大约是地球半径的60倍，地球表面的重力加速度为g，根据牛顿的猜想，月球绕地球公转的周期为（）

A、 $30 π \sqrt{\frac{r}{g}}$ B、 $30 π \sqrt{\frac{g}{r}}$ C、 $120 π \sqrt{\frac{r}{g}}$ D、 $120 π \sqrt{\frac{g}{r}}$

查看试题解析
4. 如图所示，1、2轨道分别是天宫二号飞船在变轨前后的轨道，下列说法正确的是（）

A、飞船从1轨道变到2轨道要点火加速 B、飞船在1轨道周期大于2轨道周期 C、飞船在1轨道速度大于2轨道 D、飞船在1轨道加速度大于2轨道

查看试题解析
5. 如图所示，一光滑绝缘轨道水平放置，直径上有 $A$ 、 $B$ 两点， $A O = 2 cm ， O B = 4 cm$ ，在 $A B$ 固定两个带电量分别为 $Q_{1} 、 Q_{2}$ 的正电荷，现有一个带正电小球静置于轨道内侧 $P$ 点（小球可视为点电荷），已知 $A P ： B P = n ： 1$ ，试求 $Q_{1} ： Q_{2}$ 是多少（）

A、 $2 n^{2} ： 1$ B、 $4 n^{2} ： 1$ C、 $2 n^{3} ： 1$ D、 $4 n^{3} ： 1$

查看试题解析
6. 如图所示，工人利用滑轮组将重物缓慢提起，下列说法正确的是（）

A、工人受到的重力和支持力是一对平衡力 B、工人对绳的拉力和绳对工人的拉力是一对作用力与反作用力 C、重物缓慢拉起过程，绳子拉力变小 D、重物缓慢拉起过程，绳子拉力不变

查看试题解析
7. AB、CD两块正对的平行金属板与水平面成30°角固定，竖直截面如图所示。两板间距10cm，电荷量为 $1.0 \times 10^{- 8} C$ 、质量为 $3.0 \times 10^{- 4} kg$ 的小球用长为5cm的绝缘细线悬挂于A点。闭合开关S，小球静止时，细线与AB板夹角为30°；剪断细线，小球运动到CD板上的M点（未标出），则（）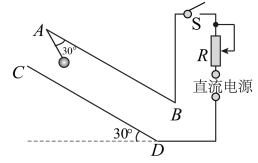

A、MC距离为 $5 \sqrt{3} cm$ B、电势能增加了 $\frac{3}{4} \sqrt{3} \times 10^{- 4} J$ C、电场强度大小为 $\sqrt{3} \times 10^{4} N / C$ D、减小R的阻值，MC的距离将变大

查看试题解析
8. 如图所示，水平面上固定两排平行的半圆柱体，重为G的光滑圆柱体静置其上，a、b为相切点， $∠ a O b = 90 °$ ，半径Ob与重力的夹角为37°。已知 $\sin 37 ° = 0.6$ ， $\cos 37 ° = 0.8$ ，则圆柱体受到的支持力F、F大小为（）

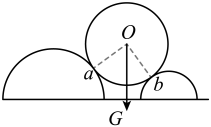A、 $F_{a} = 0.6 G$ ， $F_{b} = 0.4 G$ B、 $F_{a} = 0.4 G$ ， $F_{b} = 0.6 G$ C、 $F_{a} = 0.8 G$ ， $F_{b} = 0.6 G$ D、 $F_{a} = 0.6 G$ ， $F_{b} = 0.8 G$

查看试题解析
9. 木星的卫星中，木卫一、木卫二、木卫三做圆周运动的周期之比为 $1 ： 2 ： 4$ 。木卫三周期为T ，公转轨道半径是月球绕地球轨道半径r的n倍。月球绕地球公转周期为 $T_{0}$ ，则（）

A、木卫一轨道半径为 $\frac{n}{16} r$ B、木卫二轨道半径为 $\frac{n}{2} r$ C、周期T与T₀之比为 $n^{\frac{3}{2}}$ D、木星质量与地球质量之比为 $\frac{T_{0}^{2}}{T^{2}} n^{3}$

查看试题解析
10. 2022年12月8日，地球恰好运行到火星和太阳之间，且三者几乎排成一条直线，此现象被称为“火星冲日”。火星和地球几乎在同一平面内沿同一方向绕太阳做圆周运动，火星与地球的公转轨道半径之比约为3：2，如图所示。根据以上信息可以得出（）

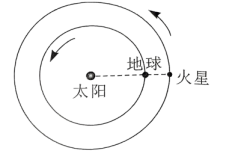A、火星与地球绕太阳运动的周期之比约为27：8 B、当火星与地球相距最远时，两者的相对速度最大 C、火星与地球表面的自由落体加速度大小之比约为9：4 D、下一次“火星冲日”将出现在2023年12月8日之前

查看试题解析
11. 安培通过实验研究，发现了电流之间相互作用力的规律。若两段长度分别为 △L₁和 △L₂、电流大小分别为I₁和I₂ 的平行直导线间距为r 时，相互作用力的大小可以表示为 $F = k \frac{I_{1} I_{2} △ L_{1} △ L_{2}}{r^{2}}$ 。比例系数k 的单位是（）

A、 kg •m/(s²•A) B、 kg •m/(s² •A²) C、kg •m²/(s³ •A) D、kg •m²/(s³ •A³)

查看试题解析
12. 如图所示，“嫦娥五号”探测器静止在月球平坦表面处。已知探测器质量为m，四条腿与竖直方向的夹角均为θ，月球表面的重力加速度为地球表面重力加速度g的 $\frac{1}{6}$ 。每条腿对月球表面压力的大小为（）

A、 $\frac{m g}{4}$ B、 $\frac{m g}{4 \cos θ}$ C、 $\frac{m g}{6 \cos θ}$ D、 $\frac{m g}{24}$

查看试题解析
13. 一同学将排球自O点垫起，排球竖直向上运动，随后下落回到O点。设排球在运动过程中所受空气阻力大小和速度大小成正比。则该排球（）

A、上升时间等于下落时间 B、被垫起后瞬间的速度最大 C、达到最高点时加速度为零 D、下落过程中做匀加速运动

查看试题解析

14. 太阳系各行星几平在同一平面内沿同一方向绕太阳做圆周运动．当地球恰好运行到某地外行星和太阳之间，且三者几乎排成一条直线的现象，称为“行星冲日”，已知地球及各地外行星绕太阳运动的轨道半径如下表：

行星名称	地球	火星	木星	土星	天王星	海王星
轨道半径 $R / AU$	1.0	1.5	5.2	9.5	19	30

则相邻两次“冲日”时间间隔约为（　　）

A、火星365天 B、火星800天 C、天王星365天 D、天王星800天

查看试题解析

二、多项选择题

15. 如图所示，原长为l的轻质弹簧，一端固定在O点，另一端与一质量为m的小球相连。小球套在竖直固定的粗糙杆上，与杆之间的动摩擦因数为0.5。杆上M、N两点与O点的距离均为l ， P点到O点的距离为 $\frac{1}{2} l$ ， OP与杆垂直。当小球置于杆上P点时恰好能保持静止。设最大静摩擦力等于滑动摩擦力，重力加速度大小为g。小球以某一初速度从M点向下运动到N点，在此过程中，弹簧始终在弹性限度内。下列说法正确的是（）

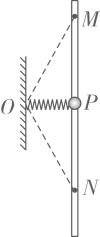A、弹簧的劲度系数为 $\frac{4 m g}{l}$ B、小球在P点下方 $\frac{1}{2} l$ 处的加速度大小为 $(3 \sqrt{2} - 4) g$ C、从M点到N点的运动过程中，小球受到的摩擦力先变小再变大 D、从M点到P点和从P点到N点的运动过程中，小球受到的摩擦力做功相同

查看试题解析
16. 使甲、乙两条形磁铁隔开一段距离，静止于水平桌面上，甲的N极正对着乙的S极，甲的质量大于乙的质量，两者与桌面之间的动摩擦因数相等。现同时释放甲和乙，在它们相互接近过程中的任一时刻（　　）

A、甲的速度大小比乙的大 B、甲的动量大小比乙的小 C、甲的动量大小与乙的相等 D、甲和乙的动量之和不为零

查看试题解析
17. 一质量为1kg的物体在水平拉力的作用下，由静止开始在水平地面上沿x轴运动，出发点为x轴零点，拉力做的功W与物体坐标x的关系如图所示。物体与水平地面间的动摩擦因数为0.4，重力加速度大小取10m/s²。下列说法正确的是（）

A、在x = 1m时，拉力的功率为6W B、在x = 4m时，物体的动能为2J C、从x = 0运动到x = 2m，物体克服摩擦力做的功为8J D、从x = 0运动到x = 4的过程中，物体的动量最大为2kg∙m/s

查看试题解析
18. 如图，固定在竖直面内的光滑轨道ABC由直线段AB和圆弧段BC组成，两段相切于B点，AB段与水平面夹角为θ，BC段圆心为O，最高点为C、A与C的高度差等于圆弧轨道的直径2R。小球从A点以初速度v₀冲上轨道，能沿轨道运动恰好到达C点，下列说法正确的是（）

A、小球从B到C的过程中，对轨道的压力逐渐增大 B、小球从A到C的过程中，重力的功率始终保持不变 C、小球的初速度 $v_{0} = \sqrt{2 g R}$ D、若小球初速度v₀增大，小球有可能从B点脱离轨道

查看试题解析
19. 如图，光滑水平地面上有一质量为 $2 m$ 的小车在水平推力 $F$ 的作用下加速运动。车厢内有质量均为 $m$ 的A、B两小球，两球用轻杆相连，A球靠在光滑左壁上，B球处在车厢水平底面上，且与底面的动摩擦因数为 $μ$ ，杆与竖直方向的夹角为 $θ$ ，杆与车厢始终保持相对静止假设最大静摩擦力等于滑动摩擦力。下列说法正确的是（）

A、若B球受到的摩擦力为零，则 $F = 2 m g \tan θ$ B、若推力 $F$ 向左，且 $\tan θ \leq μ$ ，则 $F$ 的最大值为 $2 m g \tan θ$ C、若推力 $F$ 向左，且 $μ < \tan θ \leq 2 μ$ ，则 $F$ 的最大值为 $4 m g (2 μ - \tan θ)$ D、若推力 $F$ 向右，且 $\tan θ > 2 μ$ ，则 $F$ 的范围为 $4 m g (\tan θ - 2 μ) \leq F \leq 4 m g (\tan θ + 2 μ)$

查看试题解析
20. 如图，一质量为M、长为l的木板静止在光滑水平桌面上，另一质量为m的小物块（可视为质点）从木板上的左端以速度v₀开始运动。已知物块与木板间的滑动摩擦力大小为f，当物块从木板右端离开时（）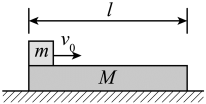

A、木板的动能一定等于fl B、木板的动能一定小于fl C、物块的动能一定大于 $\frac{1}{2} m v_{0}^{2} - f l$ D、物块的动能一定小于 $\frac{1}{2} m v_{0}^{2} - f l$

查看试题解析
21. 用水平拉力使质量分别为m_甲、m_乙的甲、乙两物体在水平桌面上由静止开始沿直线运动，两物体与桌面间的动摩擦因数分别为μ_甲和μ_乙。甲、乙两物体运动后，所受拉力F与其加速度a的关系图线如图所示。由图可知（）

A、m_甲<m_乙 B、m_甲>m_乙 C、μ_甲<μ_乙 D、μ_甲>μ_乙

查看试题解析

三、非选择题

22. 螺旋星系中有大量的恒星和星际物质，主要分布在半径为R的球体内，球体外仅有极少的恒星。球体内物质总质量为M，可认为均匀分布，球体内外的所有恒星都绕星系中心做匀速圆周运动，恒星到星系中心的距离为r ，引力常量为G。

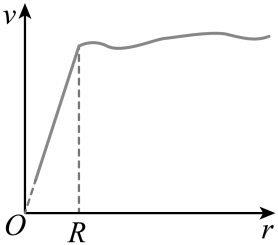(1)、求 $r > R$ 区域的恒星做匀速圆周运动的速度大小v与r的关系；

(2)、根据电荷均匀分布的球壳内试探电荷所受库仑力的合力为零，利用库仑力与万有引力的表达式的相似性和相关力学知识，求 $r \leq R$ 区域的恒星做匀速圆周运动的速度大小v与r的关系；

(3)、科学家根据实测数据，得到此螺旋星系中不同位置的恒星做匀速圆周运动的速度大小v随r的变化关系图像，如图所示，根据在 $r > R$ 范围内的恒星速度大小几乎不变，科学家预言螺旋星系周围（ $r > R$ ）存在一种特殊物质，称之为暗物质。暗物质与通常的物质有引力相互作用，并遵循万有引力定律，求 $r = n R$ 内暗物质的质量 $M^{'}$ 。

查看试题解析
23. 如图所示，物块A和木板B置于水平地面上，固定光滑弧形轨道末端与B的上表面所在平面相切，竖直挡板P固定在地面上。作用在A上的水平外力，使A与B以相同速度 $v_{0}$ 向右做匀速直线运动。当B的左端经过轨道末端时，从弧形轨道某处无初速度下滑的滑块C恰好到达最低点，并以水平速度v滑上B的上表面，同时撤掉外力，此时B右端与P板的距离为s。已知 $v_{0} = 1 m/s$ ， $v =4m/s$ ， $m_{A} = m_{C} = 1 kg$ ， $m_{B} = 2 kg$ ， A与地面间无摩擦，B与地面间动摩擦因数 $μ_{1} = 0.1$ ， C与B间动摩擦因数 $μ_{2} = 0.5$ ， B足够长，使得C不会从B上滑下。B与P、A的碰撞均为弹性碰撞，不计碰撞时间，取重力加速度大小 $g = 10 m / s^{2}$ 。

(1)、求C下滑的高度H；

(2)、与P碰撞前，若B与C能达到共速，且A、B未发生碰撞，求s的范围；

(3)、若 $s = 0.48 m$ ，求B与P碰撞前，摩擦力对C做的功W；

(4)、若 $s = 0.48 m$ ，自C滑上B开始至A、B、C三个物体都达到平衡状态，求这三个物体总动量的变化量 $Δ p$ 的大小。

查看试题解析
24. 如图所示，竖直放置在水平桌面上的左右两汽缸粗细均匀，内壁光滑，横截面积分别为S、 $2 S$ ，由体积可忽略的细管在底部连通。两汽缸中各有一轻质活塞将一定质量的理想气体封闭，左侧汽缸底部与活塞用轻质细弹簧相连。初始时，两汽缸内封闭气柱的高度均为H ，弹簧长度恰好为原长。现往右侧活塞上表面缓慢添加一定质量的沙子，直至右侧活塞下降 $\frac{1}{3} H$ ，左侧活塞上升 $\frac{1}{2} H$ 。已知大气压强为 $p_{0}$ ，重力加速度大小为g ，汽缸足够长，汽缸内气体温度始终不变，弹簧始终在弹性限度内。求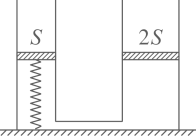

(1)、最终汽缸内气体的压强。

(2)、弹簧的劲度系数和添加的沙子质量。

查看试题解析
25. 某同学利用测质量的小型家用电子秤，设计了测量木块和木板间动摩擦因数 $μ$ 的实验。
如图（a）所示，木板和木块A放在水平桌面上，电子秤放在水平地面上，木块A和放在电子秤上的重物B通过跨过定滑轮的轻绳相连。调节滑轮，使其与木块A间的轻绳水平，与重物B间的轻绳竖直。在木块A上放置n（ $n = 0 ， 1 ， 2 ， 3 ， 4 ， 5$ ）个砝码（电子秤称得每个砝码的质量 $m_{0}$ 为 $20 ． 0g$ ），向左拉动木板的同时，记录电子秤的对应示数m。

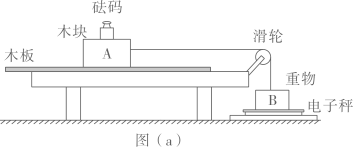
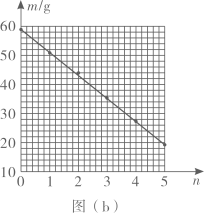(1)、实验中，拉动木板时（填“必须”或“不必”）保持匀速。

(2)、用 $m_{A}$ 和 $m_{B}$ 分别表示木块A和重物B的质量，则m和 $m_{A} 、 m_{B} 、 m_{0} 、 μ 、 n$ 所满足的关系式为 $m =$ 。

(3)、根据测量数据在坐标纸上绘制出 $m - n$ 图像，如图（b）所示，可得木块A和木板间的动摩擦因数 $μ =$ （保留2位有效数字）。

查看试题解析
26. 如图，质量m₁=1kg 的木板静止在光滑水平地面上，右侧的竖直墙面固定一劲度系数k=20N/m 的轻弹簧，弹簧处于自然状态。质量m₂=4kg 的小物块以水平向右的速度 $v_{0} = \frac{5}{4} m / s$ 滑上木板左端，两者共速时木板恰好与弹簧接触。木板足够长，物块与木板间的动摩擦因数μ=0.1，最大静摩擦力等于滑动摩擦力。弹簧始终处在弹性限度内，弹簧的弹性势能 Ep与形变量x 的关系为 $E_{p} = \frac{1}{2} k x^{2}$ 。取重力加速度g=10m/s² ，结果可用根式表示。

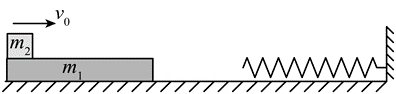(1)、求木板刚接触弹簧时速度v，的大小及木板运动前右端距弹簧左端的距离x₁。

(2)、求木板与弹簧接触以后，物块与木板之间即将相对滑动时弹簧的压缩量x₂及此时木板速度v₂的大小。

(3)、已知木板向右运动的速度从v₂减小到0所用时间为t₀。求木板从速度为v₂ 时到之后与物块加速度首次相同时的过程中，系统因摩擦转化的内能△U（用t表示）。

查看试题解析
27. 如图，一竖直固定的长直圆管内有一质量为M的静止薄圆盘，圆盘与管的上端口距离为l，圆管长度为20l。一质量为 $m = \frac{1}{3} M$ 的小球从管的上端口由静止下落，并撞在圆盘中心，圆盘向下滑动，所受滑动摩擦力与其所受重力大小相等。小球在管内运动时与管壁不接触，圆盘始终水平，小球与圆盘发生的碰撞均为弹性碰撞且碰撞时间极短。不计空气阻力，重力加速度大小为g。求：

(1)、第一次碰撞后瞬间小球和圆盘的速度大小；

(2)、在第一次碰撞到第二次碰撞之间，小球与圆盘间的最远距离；

(3)、圆盘在管内运动过程中，小球与圆盘碰撞的次数。

查看试题解析