【备考2024年】中考数学杭州卷真题变式分层精准练第16题
试卷更新日期:2023-07-26 类型:二轮复习
一、原题
-
1. 如图,在中, , 点分别在边 , 上,连接 , 已知点和点关于直线对称.设 , 若 , 则(结果用含的代数式表示).

二、基础
-
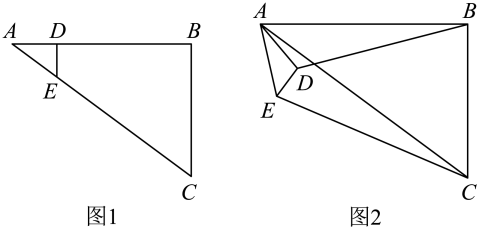
2. 如图1,在中, , , , D是上一点,且 , 过点D作交于E,将绕A点顺时针旋转到图2的位置.则图2中的值为 .
 3. 如图,在平行四边形ABCD中,E是线段AB上一点,连结AC、DE交于点F.若 , 则 .
3. 如图,在平行四边形ABCD中,E是线段AB上一点,连结AC、DE交于点F.若 , 则 . 4. 如图,在平行四边形中,点在上,交于点 , 若 , 则 .
4. 如图,在平行四边形中,点在上,交于点 , 若 , 则 . 5. 已知 , 与相交于点 , 其中点 , 分别是 , 的中点,若 , 则的值为 .
5. 已知 , 与相交于点 , 其中点 , 分别是 , 的中点,若 , 则的值为 . 6. 如图,在中,点D、E分别在边上, , , 如果 , , 那么的值是 .
6. 如图,在中,点D、E分别在边上, , , 如果 , , 那么的值是 .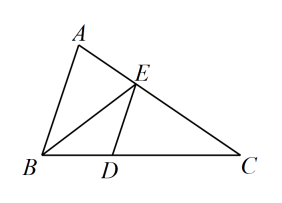 7. 如图,在中,的平分线交于点F.点D,E分别在 , 上,连接交于点G.若 , , 则 .
7. 如图,在中,的平分线交于点F.点D,E分别在 , 上,连接交于点G.若 , , 则 . 8. 如图,已知、是的中线,和交于点 , 当时,那么的值等于 .
8. 如图,已知、是的中线,和交于点 , 当时,那么的值等于 .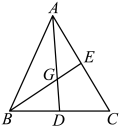 9. 如图,是半的直径,点C是弧的中点,点E是弧的中点,连接交于点F,则 .
9. 如图,是半的直径,点C是弧的中点,点E是弧的中点,连接交于点F,则 . 10. 如图,在中,D是上一点, , 则 .
10. 如图,在中,D是上一点, , 则 .
三、提高
-
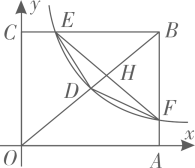
11. 2002年的国际数学家大会在中国北京举行,这是21世纪全世界数学家的第一次大聚会.这次大会的会徽选定了我国古代数学家赵爽用来证明勾股定理的弦图,世人称之为“赵爽弦图”.如图,用四个全等的直角三角形(Rt△AHB≌Rt△BEC≌Rt△CFD≌Rt△DGA)拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH,连接AC和EG,AC与DF、EG、BH分别相交于点P、O、Q,若BE∶EQ=3∶2,则的值是 .
 12. 如图,在Rt中, , 将绕点逆时针方向旋转 , 得到.连接 , 交AC于点 , 则的值为.
12. 如图,在Rt中, , 将绕点逆时针方向旋转 , 得到.连接 , 交AC于点 , 则的值为.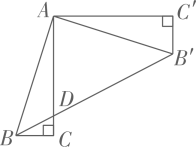 13. 如图,在中, , CD平分交AB于点D,过D作交AC于点E,将沿DE折叠得到 , DF交AC于点G.若 , 则.
13. 如图,在中, , CD平分交AB于点D,过D作交AC于点E,将沿DE折叠得到 , DF交AC于点G.若 , 则. 14. 希腊数学家海伦给出了挖掘直线隧道的方法:如图,是两侧山脚的入口,从出发任作线段 , 过作 , 然后依次作垂线段 , 直到接近点,作于点 . 每条线段可测量,长度如图所示.分别在 , 上任选点 , 作 , , 使得 , 此时点共线.挖隧道时始终能看见处的标志即可.
14. 希腊数学家海伦给出了挖掘直线隧道的方法:如图,是两侧山脚的入口,从出发任作线段 , 过作 , 然后依次作垂线段 , 直到接近点,作于点 . 每条线段可测量,长度如图所示.分别在 , 上任选点 , 作 , , 使得 , 此时点共线.挖隧道时始终能看见处的标志即可. (1)、 km.(2)、 = .15. 如图, , AB=a,CD=b, . 则EF= .
(1)、 km.(2)、 = .15. 如图, , AB=a,CD=b, . 则EF= . 16. 如图,线段轴,双曲线与分别经过点 , 点 , 过点作轴的垂线段,垂足为 , 连接 , 与相交于点 , 若 , 则:的值为 .
16. 如图,线段轴,双曲线与分别经过点 , 点 , 过点作轴的垂线段,垂足为 , 连接 , 与相交于点 , 若 , 则:的值为 . 17. 如图,在中, , 点D为中点, , 则的值为 .
17. 如图,在中, , 点D为中点, , 则的值为 . 18. 如图,在正方形内部作等边 , 交于F点,过E作 , 分别交于点G,H.则的值是 .
18. 如图,在正方形内部作等边 , 交于F点,过E作 , 分别交于点G,H.则的值是 .
四、培优
-
19. 如图,在中, , , 将绕着点C按顺时针旋转得到 , 连接BD交于在E,则 .
 20. 如图,在中, , , 点D为上一动点,连接 , 将沿翻折得到 , 交于点G, , 且 , 则 .
20. 如图,在中, , , 点D为上一动点,连接 , 将沿翻折得到 , 交于点G, , 且 , 则 .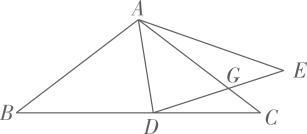 21. 如图,四边形为正方形纸片,E是边的中点,连接 , P是边上一点,将纸片沿着折叠,使点D落在上的F点处,则为 .
21. 如图,四边形为正方形纸片,E是边的中点,连接 , P是边上一点,将纸片沿着折叠,使点D落在上的F点处,则为 .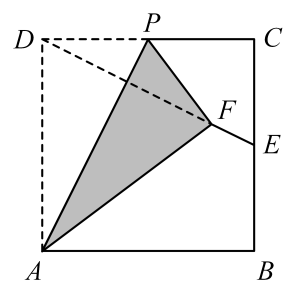
-