【备考2024年】中考数学杭州卷真题变式分层精准练第15题

试卷更新日期：2023-07-26 类型：二轮复习

进入出卷网下载

一、原题

1. 在“探索一次函数y=kx+b的系数k、b与图象的关系”活动中，老师给出了直角坐标系中的三个点：A（0，2），B（2，3），C（3，1）．同学们画出了经过这三个点中每两个点的一次函数的图象，并得到对应的函数表达式 $y_{1} = k_{1} x + b_{1} ， y_{2} = k_{2} x + b_{2} ， y_{3} = k_{3} x + b_{3}$ ．分别计算 $k_{1} + b_{1}$ ， $k_{2} + b_{2} ， k_{3} + b_{3}$ 的值，其中最大的值等于．

查看试题解析

二、基础

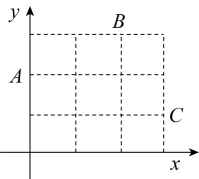
2. 如图，点A（﹣1，m）在直线y=2x+3上，连结OA，∠AOB=90°，点B在直线y=﹣x+b上，OA=OB，则b= ．

查看试题解析
3. 若一次函数 $y = 2 x + b (k \neq 0)$ 的图象向下平移3个单位后经过点 $A (1 ， 4)$ ，则b的值为．

查看试题解析
4. 如图3，在平面直角坐标系 $x O y$ 内，已知点 $G (- 3 ， 1)$ ， $A (- 1 ， 3)$ ， $B (- 4 ， 0)$ ，如果 $⊙ C$ 是以线段 $A B$ 为直径的圆，那么点G与 $⊙ C$ 的最短距离为．

查看试题解析
5. 平面直角坐标系中，点 $A (1 ， 3) ， B (- 1 ， - 1) ， C (3 ， a)$ 在同一条直线上，则a的值为.

查看试题解析
6. 已知点 $A (3 ， 4)$ ， $B (- 1 ， - 2)$ ，将线段 $A B$ 平移到线段 $C D$ ，若点A的对应点C落在x轴上，点B的对应点D落在y轴上，则线段 $A B$ 与y轴的交点P经过平移后对应点的坐标为.

查看试题解析
7. 已知三点 $(1 ， - 1)$ ， $(2 ， - 3)$ ， $(a ， 7)$ 在同一条直线上，则a的值为

查看试题解析
8. 若点A(-5，m)，B(n，4)都在函数y=x+b的图象上，则m+n的值为。

查看试题解析
9. 已知，一次函数 $y = k x + b$ ，当 $2 \leq x \leq 5$ 时， $- 3 \leq y \leq 6$ ．则 $k + b$ 的值是．

查看试题解析

三、提高

10. 如图，在平面直角坐标系中，A（3，0），B（0，4），C（2，0），D（0，1），连接AD、BC交于点E，则三角形ABE的面积为．

查看试题解析
11. 图形的变换就是点的变换，例如将直线y＝3x+1向右平移2个单位，求平移后直线的解析式，我们不妨先在直线y＝﹣3x+1上任意取两点（0，1）和（1，4），平移后这两点分别为（2，1）和（3，4），则平移后直线的解析式为y＝3x﹣5，现将直线y＝﹣3x+2关于x轴对称，则对称后直线的解析式为．

查看试题解析
12. 图形的变换就是点的变换，例如将直线 $y = 3 x + 1$ 向右平移2个单位，求平移后直线的解析式，我们不妨先在直线 $y = 3 x + 1$ 上任意取两点 $(0 ， 1)$ 和 $(1 ， 4)$ ，平移后这两点分别为 $(2 ， 1)$ 和 $(3 ， 4)$ ，则平移后直线的解析式为 $y = 3 x - 5$ ，现将直线 $y = - 3 x + 2$ 关于 $x$ 轴对称，则对称后直线的解析式为．

查看试题解析
13. 反比例函数y= $\frac{k}{x}$ 的图象与一次函数y=mx+n的图象交于两点（a，a-1），（a-7，-a），则不等式 $\frac{k}{x}$ >mx+n的解集为

查看试题解析
14. 如图，四个白色全等直角三角形与四个黑色全等三角形按如所示方式摆放成“风车”型，且黑色三角形的顶点E、F、G、H分别在白色直角三角形的斜边上，已知∠ABO＝90°，OB＝3，AB＝4，若点A、E、D在同一直线上，则OE的长为．

查看试题解析
15. 在平面直角坐标系中，已知A、B、C、D四点的坐标依次为（0，0）、（6，0）（8，6）、（2，6），若一次函数y=mx﹣6m的图象将四边形ABCD的面积分成1：3两部分，则m的值为.

查看试题解析
16. 下表分别给出了一次函数y₁＝k₁x＋b₁与y₂＝k₂x＋b₂图象上部分点的横坐标x和纵坐标y的对应值.则当x时，y₁＞y₂.
x
-4
-3
-2
-1
y₁
-9
-6
-3
0
x
-4
-3
-2
-1
y₂
-1
-2
-3
-4

查看试题解析
17. 如图，平面直角坐标系中，△ABC的顶点坐标分别是A(1，1)，B(3，1)，C(2，2)，当直线y＝ $\frac{1}{2}$ x＋b与△ABC有交点时，b的取值范围是．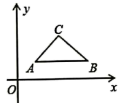

查看试题解析

四、培优

18. 如图，在平面直角坐标系中，点A、B的坐标分别为 $(- \frac{\sqrt{3}}{2} ， 0)$ ， $(\frac{\sqrt{3}}{2} ， 1)$ ，连接 $A B$ ，以 $A B$ 为边向上作等边三角形 $A B C$ ，则线段 $B C$ 所在直线的函数表达式为．

查看试题解析
19. 如图，在平面直角坐标系中，一次函数 $y = k x + b$ 的图象经过正方形OABC的顶点A和C，已知点A的坐标为 $(1 ， - 3)$ ，则b的值为．

查看试题解析
20. 如图，正方形 $A_{1} B_{1} C_{1} O$ ， $A_{2} B_{2} C_{2} C_{1}$ ， $A_{3} B_{3} C_{3} C_{2}$ …按如图所示的方式放置．点 $A_{1} 、 A_{2} 、 A_{3}$ …和点 $C_{1} 、 C_{2} 、 C_{3}$ …分别在直线 $y = k x + b$ （ $k > 0$ 和x轴上，已知点 $B_{1} (1 ， 1) ， B_{2} (3 ， 2)$ ，则 $B_{12}$ 的坐标是．

查看试题解析
21. 对于坐标平面内的点，先将该点向右平移1个单位，再向上平移2个单位，这种点的运动称为点的斜平移，如点 $P (2 ， 3)$ 经1次斜平移后的点的坐标为 $(3 ， 5)$ ．已知点 $A$ 的坐标为 $(1 ， 0)$ ．如图，点 $M$ 是直线 $l$ 上的一点，点 $A$ 关于点 $M$ 的对称点为点 $B$ ，点 $B$ 关于直线 $l$ 的对称点为点 $C$ ．若点 $B$ 由点 $A$ 经 $n$ 次斜平移后得到，且点 $C$ 的坐标为 $(7 ， 6)$ ，则点 $B$ 的坐标为．

查看试题解析

x		-4		-3		-2		-1
y₁		-9		-6		-3		0
x	-4		-3		-2		-1
y₂	-1		-2		-3		-4