【备考2024年】中考数学杭州卷真题变式分层精准练第12题
试卷更新日期:2023-07-26 类型:二轮复习
一、原题
-
1. 如图,点分别在的边上,且 , 点在线段的延长线上.若 , , 则 .
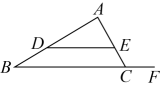
二、基础
-
2. 如图,直线 , , , 则 .
 3. 在螳螂的示意图中, , 是等腰三角形, , 则的度数是 .
3. 在螳螂的示意图中, , 是等腰三角形, , 则的度数是 .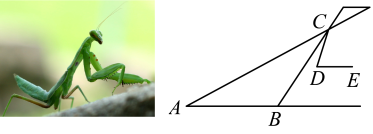 4. 已知直线 , 将一块含有角的直角三角板按如图方式放置,其中斜边与直线相交于点 , AB与直线n的交点标为点E .若 , 则的度数为 .
4. 已知直线 , 将一块含有角的直角三角板按如图方式放置,其中斜边与直线相交于点 , AB与直线n的交点标为点E .若 , 则的度数为 . 5. 如图,已知直线 , 点A在直线a上,点B、C在直线b上,点P在线段上,如果 , , 那么 .
5. 如图,已知直线 , 点A在直线a上,点B、C在直线b上,点P在线段上,如果 , , 那么 . 6. 如图,直线 , 的平分线交直线于点D,若 , 则的度数为 .
6. 如图,直线 , 的平分线交直线于点D,若 , 则的度数为 . 7. 如图,将一块含45°的直角三角板的直角顶点放在直尺的一边上,当∠1=35°时,则∠2的度数是 .
7. 如图,将一块含45°的直角三角板的直角顶点放在直尺的一边上,当∠1=35°时,则∠2的度数是 . 8. 如图,点D在的平分线OC上,点E在OA上, , , 则 的度数为 .
8. 如图,点D在的平分线OC上,点E在OA上, , , 则 的度数为 . 9. 如图,若 , 则∠1+∠3-∠2的度数为
9. 如图,若 , 则∠1+∠3-∠2的度数为 10. 某城市几条道路的位置关系如图所示,道路 , 道路与的夹角 . 城市规划部门想新修一条道路BF,要求 , 则的度数为 .
10. 某城市几条道路的位置关系如图所示,道路 , 道路与的夹角 . 城市规划部门想新修一条道路BF,要求 , 则的度数为 . 11. 一副三角板如图摆放,两斜边平行,则°.
11. 一副三角板如图摆放,两斜边平行,则°.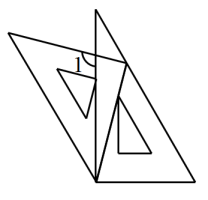 12. 一副三角板如图所示摆放,且 ,则 的度数为 .
12. 一副三角板如图所示摆放,且 ,则 的度数为 .
 13. 如图一副直角三角板如图放置 , , ,则求 .
13. 如图一副直角三角板如图放置 , , ,则求 .
三、提高
-
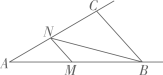
14. 如图,在中, , , M是射线上的一个动点,过点M作交射线于点N,连接 , 若中有两个角相等,则的度数可能是.
 15. 如图是国家级非物质文化遗产——“抖空竹”.在“抖空竹”的一个瞬间如图①所示,若将图①抽象成图②的数学问题: , , , 则的大小是度.
15. 如图是国家级非物质文化遗产——“抖空竹”.在“抖空竹”的一个瞬间如图①所示,若将图①抽象成图②的数学问题: , , , 则的大小是度.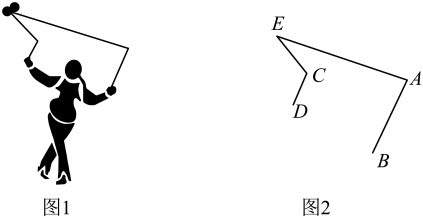 16. 如图、在菱形ABCD中,∠ADC=128°,P是对角线AC,BD的交点,点E在CB的延长线上,且PE=PA.则∠APE=度。
16. 如图、在菱形ABCD中,∠ADC=128°,P是对角线AC,BD的交点,点E在CB的延长线上,且PE=PA.则∠APE=度。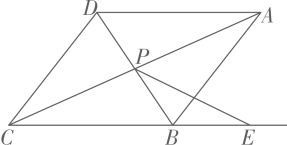 17. 线段和线段交于点 , 平分 , 点为线段上一点不与点和点重合 , 过点作 , 交线段于点 , 若则的度数为 .
17. 线段和线段交于点 , 平分 , 点为线段上一点不与点和点重合 , 过点作 , 交线段于点 , 若则的度数为 .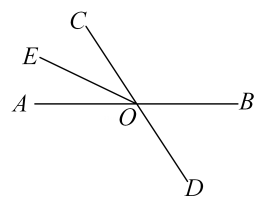 18. 如图,直线 , 将一个含角的直角三角板按如图所示的位置放置,若 , 则的度数为 .
18. 如图,直线 , 将一个含角的直角三角板按如图所示的位置放置,若 , 则的度数为 . 19. 如图, , 是的平分线,过作交于 , 作 , 垂足为 , , 则 .
19. 如图, , 是的平分线,过作交于 , 作 , 垂足为 , , 则 . 20. 如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′,BE,CD交于点F.若∠BAC=40°,则∠BFC的度数为 .
20. 如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′,BE,CD交于点F.若∠BAC=40°,则∠BFC的度数为 .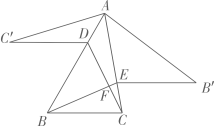 21. 如图,直线 , 点E、F分别为直线和上的点,点P为两条平行线间的一点,连接和 , 过点P作的平分线交直线于点G,过点F作 , 垂足为H,若 , 则°.
21. 如图,直线 , 点E、F分别为直线和上的点,点P为两条平行线间的一点,连接和 , 过点P作的平分线交直线于点G,过点F作 , 垂足为H,若 , 则°.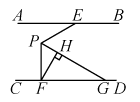
四、培优
-
22. 如图,AB∥CD, 的平分线 和 的平分线 的反向延长交于点E,且 ,则 度.
 23. 随着科技的发展,人们使用平板学习已经成为常态,它拥有的智能磁吸键盘和手写笔更是给人们带来无纸化学习新体验,如图1,当平板放在智能磁吸键盘上时,可调整平板角度,研究表明,屏幕中心在直视屏幕视线下方10°:20°时可减少视觉和肌肉骨骼不适.图2为调整示意图,即∠G=90°,∠GED=x°(10°<x<20°)时为最佳.当平板下沿落在第一个卡槽A时,键盘盖下半部分OC与键盘OP的夹角∠2=67°,键盘盖上、下半部分CD与OC的夹角∠3=134°,水平视线与屏幕视线夹角∠FED=38°,则x=;当平板下沿落在卡槽B时,∠2=53°,∠3=106°,则∠FED= .
23. 随着科技的发展,人们使用平板学习已经成为常态,它拥有的智能磁吸键盘和手写笔更是给人们带来无纸化学习新体验,如图1,当平板放在智能磁吸键盘上时,可调整平板角度,研究表明,屏幕中心在直视屏幕视线下方10°:20°时可减少视觉和肌肉骨骼不适.图2为调整示意图,即∠G=90°,∠GED=x°(10°<x<20°)时为最佳.当平板下沿落在第一个卡槽A时,键盘盖下半部分OC与键盘OP的夹角∠2=67°,键盘盖上、下半部分CD与OC的夹角∠3=134°,水平视线与屏幕视线夹角∠FED=38°,则x=;当平板下沿落在卡槽B时,∠2=53°,∠3=106°,则∠FED= .
 24. 如图,一位跑酷运动员准备以连续两次“跳跃”结束一次跑酷表演,即在水平面 AB 上跑至 B点,向上跃起至最高点 P,然后落在点 C 处,继续在水平面 CD 上跃起落在点 D,若∠ABK 和∠KCD 的平分线的反向延长线刚好交于最高点 P,∠BKC=88°,则∠P=度.
24. 如图,一位跑酷运动员准备以连续两次“跳跃”结束一次跑酷表演,即在水平面 AB 上跑至 B点,向上跃起至最高点 P,然后落在点 C 处,继续在水平面 CD 上跃起落在点 D,若∠ABK 和∠KCD 的平分线的反向延长线刚好交于最高点 P,∠BKC=88°,则∠P=度.
-