【备考2024年】中考数学杭州卷真题变式分层精准练第10题

试卷更新日期：2023-07-26 类型：二轮复习

进入出卷网下载

一、原题

1. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”．如图，在由四个全等的直角三角形（ $△ D A E ， △ A B F ， △ B C G ， △ C D H$ ）和中间一个小正方形 $E F G H$ 拼成的大正方形 $A B C D$ 中， $∠ A B F > ∠ B A F$ ，连接 $B E$ ．设 $∠ B A F = α ， ∠ B E F = β$ ，若正方形 $E F G H$ 与正方形 $A B C D$ 的面积之比为 $1 ： n ， t a n α = t a n^{2} β$ ，则 $n =$ （）

A、5 B、4 C、3 D、2

查看试题解析

二、基础

2. 下图源于我国汉代数学家赵爽的弦图，它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为 $α$ ，则 $c o s α$ 的值为（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
3. 我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”，如图所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形．如果大正方形面积为25，小正方形面积为1，则 $s i n θ =$ （）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{2}{5}$ D、 $\frac{1}{5}$

查看试题解析
4. 我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形．如果大正方形的面积是100，小正方形面积是20，则 $\sin θ \cdot \cos θ =$ （）

A、 $\frac{1}{5}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{2}{5}$

查看试题解析
5. 四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”（如图）．如果小正方形面积为49，大正方形面积为169，直角三角形中较小的锐角为θ，那么 $\sin θ$ 的值（）．

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{6}{13}$ D、 $\frac{5}{13}$

查看试题解析
6. 公元三世纪，我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125，小正方形面积是25，则（sinθ+cosθ）²＝（）

A、 $\frac{9}{5}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{3 \sqrt{5}}{5}$ D、 $\frac{1}{5}$

查看试题解析
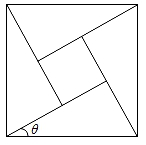7. 如图，“赵爽弦图”是吴国的赵爽创制的．以直角三角形的斜边为边长得到一个正方形，该正方形由4个全等的直角三角形再加上中间的小正方形组成，在一次游园活动中，数学小组制作了一面“赵爽弦图锣”，其中∠AEB＝90°，AB＝13cm，BE＝5cm，则阴影部分的面积是（）

A、169cm² B、25cm² C、49cm² D、64cm²

查看试题解析
8. 赵爽弦图是由4个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示）．若小正方形和大正方形的面积分别是1和5，则直角三角形两条直角边长分别为（）

A、2， $\sqrt{3}$ B、1， $\sqrt{3}$ C、2，1 D、2， $\sqrt{5}$

查看试题解析
9. 公元三世纪，我国汉代数学家赵爽在注解 $《$ 周髀算经 $》$ 时给出的“赵爽弦图”如图所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125，小正方形面积是25，则 ${(s i n θ - c o s θ)}^{2} = （）$

A、 $\frac{1}{5}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{3 \sqrt{5}}{5}$ D、 $\frac{9}{5}$

查看试题解析
10. 如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”，图中的四个直角三角形是全等的，如果大正方形ABCD的面积是小正方形EFGH面积的13倍，那么tan∠ADE的值为（）

A、 $\frac{3}{2}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{2 \sqrt{13}}{13}$

查看试题解析
11. 如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，如果大正方形的面积为16，直角三角形的面积为3，直角三角形的两直角边分别为a和b，那么 $(a + b)^{2}$ 的值为（）

A、18 B、22 C、28 D、36

查看试题解析
12. 如图，四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”．若直角三角形的两条直角边长分别为2和3，则大正方形与小正方形的面积之比为（）

A、9：2 B、1：13 C、1：14 D、2：15

查看试题解析

三、提高

13. 勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理，在我国古书《周牌算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”（如图①），后人称之为“赵爽弦图”，流传至今，如图①是用四个全等的直角三角形拼成一个正方形，利用面积法可以证明勾股定理.如图2连接EG并延长交D的延长线于点M，如tanM＝ $\frac{1}{2}$ ，则 $\frac{H G}{G M}$ 的值为（）

A、2 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、1.4

查看试题解析
14. 我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，它是由四个全等的直角三角形与中间的小正方形 $E F G H$ 拼成的一个大正方形 $A B C D$ ，连接 $A C$ ，交 $B E$ 于点 $P$ ，如图所示，若正方形 $A B C D$ 的面积为 $28$ ， $A E + E B = 7$ ，则 $S_{△ C F P} - S_{△ A E P}$ 的值是（　　）

A、3 B、3.5 C、4 D、7

查看试题解析
15. 如图1，四个全等的直角三角形围成一个大正方形，中间是个小正方形，这个图形是我国汉代赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”.在弦图中（如图2）连结AF，DE，并延长DE交AF于点K，连结KG. 若AH=2DH = $2 \sqrt{2}$ ，则KG的长为（）

A、2 B、 $\frac{3}{2} \sqrt{2}$ C、 $\sqrt{5}$ D、 $2 \sqrt{2}$

查看试题解析
16. 汉代数学家赵爽为了证明勾股定理，构造了一副“弦图”，后人称其为“赵爽弦图”．如图，大正方形 $A B C D$ 由四个全等的直角三角形和一个小正方形组成，若 $∠ A D E = ∠ A E D$ ， $A D = 2 \sqrt{5}$ ，则 $△ A D E$ 的面积为（）

A、6 B、5 C、 $2 \sqrt{5}$ D、 $2 \sqrt{10}$

查看试题解析
17. 如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH．连结BD交AF，CH于点N，P．若DE=3AE，正方形ABCD的面积为10，则△DHP，△NPG，△BNF的面积和为（）

A、 $1 + \sqrt{2}$ B、 $\sqrt{2}$ C、 $\frac{9}{4}$ D、2

查看试题解析
18. 我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图（1）所示）.图（2）由弦图变化得到，它是由八个全等的直角三角形拼接而成的记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S₁ ， S₂ ， S₃ ，若EF＝4，则S₁+S₂+S₃的值是（）

A、32 B、38 C、48 D、80

查看试题解析

四、培优

19. 如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH.连接EB，EG，延长EG交CD于点M，若∠BEM=90°，则BE：EM的值为（）

A、1：2 B、3：4 C、5：6 D、5：12

查看试题解析
20. 如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，它是由四个全等的直角三角形与中间的小正方形EFGH拼成的一个大正方形ABCD连结AG并延长交BC于点M.若 $\frac{A E}{B E}$ ＝ $\frac{1}{3}$ ，则 $\frac{C M}{B M}$ 的值为（）

A、 $\frac{3}{10}$ B、 $\frac{2}{7}$ C、 $\frac{1}{4}$ D、 $\frac{2}{9}$

查看试题解析
21. 如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图，它是由四个全等的直角三角形和一个小正方形EFGH组成，恰好拼成一个大正方形ABCD.连结EG并延长交BC于点M.若AB＝ $\sqrt{13}$ ，EF=1，则GM的长为（）

A、 $\frac{2 \sqrt{2}}{5}$ B、 $\frac{2 \sqrt{2}}{3}$ C、 $\frac{3 \sqrt{2}}{4}$ D、 $\frac{4 \sqrt{2}}{5}$

查看试题解析
22. 赵爽弦图由四个全等的直角三角形所组成，形成一个大正方形，中间是一个小正方形（如图所示）．某次课后服务拓展学习上，小浔绘制了一幅赵爽弦图，她将EG延长交CD于点Ｉ．记小正方形EFGＨ的面积为Ｓ₁ ，大正方形ABCD的面积为Ｓ₂ ，若DＩ＝2，CＩ＝1，Ｓ₂＝5Ｓ₁ ，则GＩ的值是（）

A、 $\frac{\sqrt{10}}{5}$ B、 $\frac{9}{20} \sqrt{2}$ C、 $\frac{\sqrt{5}}{8}$ D、 $\frac{3}{4}$

查看试题解析