北师大版数学九年级上册同步练习—— 第四章 《图形的相似》8.图形的位似(1)
试卷更新日期:2023-07-26 类型:同步测试
一、选择题
-
1. 如图,在正方形网格中,与位似,则下列说法正确的是( )
 A、位似中心是点 B、位似中心是点 C、位似比为 D、位似比为2. 如图,在方格纸上,以点O为位似中心,把线段缩小到原来的 , 则点A的对应点为( )
A、位似中心是点 B、位似中心是点 C、位似比为 D、位似比为2. 如图,在方格纸上,以点O为位似中心,把线段缩小到原来的 , 则点A的对应点为( )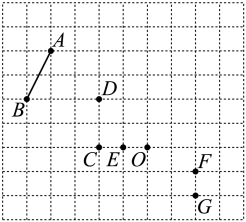 A、点D或点G B、点E或点F C、点D或点F D、点E或点G3. 如图,与位似,位似中心为点.若的周长与的周长比为 , 则的值为( )
A、点D或点G B、点E或点F C、点D或点F D、点E或点G3. 如图,与位似,位似中心为点.若的周长与的周长比为 , 则的值为( ) A、 B、 C、 D、4. 如图,与位似,点O为位似中心,已知 , 的面积为1,则的面积是( )
A、 B、 C、 D、4. 如图,与位似,点O为位似中心,已知 , 的面积为1,则的面积是( )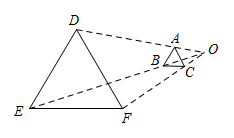 A、3 B、4 C、9 D、165. 每年秋季开学,学校组织同学们进行视力测试,如图是视力表的一部分,其中开口向上的两个“”之间的变换是( )
A、3 B、4 C、9 D、165. 每年秋季开学,学校组织同学们进行视力测试,如图是视力表的一部分,其中开口向上的两个“”之间的变换是( ) A、平移 B、对称 C、位似 D、旋转6. 如图,以点O为位似中心,作四边形的位似图形 , 已知 , 若四边形的面积是2,则四边形的面积是( )
A、平移 B、对称 C、位似 D、旋转6. 如图,以点O为位似中心,作四边形的位似图形 , 已知 , 若四边形的面积是2,则四边形的面积是( )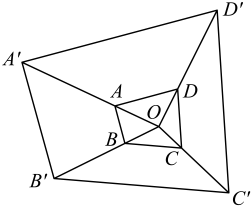 A、4 B、6 C、16 D、187. 如图,以点O为位似中心,将放大后得到 , , , 则等于( )
A、4 B、6 C、16 D、187. 如图,以点O为位似中心,将放大后得到 , , , 则等于( )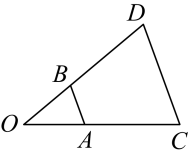 A、 B、 C、 D、8. 如图,与位似,点为位似中心,相似比为2:3.若的周长为4,则的周长是( )
A、 B、 C、 D、8. 如图,与位似,点为位似中心,相似比为2:3.若的周长为4,则的周长是( ) A、4 B、6 C、9 D、16
A、4 B、6 C、9 D、16二、填空题
-
9. 如图,和是以点为位似中心的位似图形,点在线段上.若 , 则和的周长之比为 .
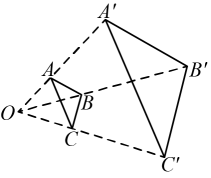 10. 如图所示△ABC和△A'B'C'是以点O为位似中心的位似图形,已知点C'是OC的三等分点,则△A'B'C'与△ABC的面积之比为 .
10. 如图所示△ABC和△A'B'C'是以点O为位似中心的位似图形,已知点C'是OC的三等分点,则△A'B'C'与△ABC的面积之比为 . 11. 如图,以点О为位似中心,将缩小得到 , 若 , 的周长为2,则的周长为 .
11. 如图,以点О为位似中心,将缩小得到 , 若 , 的周长为2,则的周长为 . 12. 如图,以点O为位似中心,将ΔOAB放大后得到ΔOCD,若OA=2, , 则AC=.
12. 如图,以点O为位似中心,将ΔOAB放大后得到ΔOCD,若OA=2, , 则AC=.
三、解答题
-
13. 如图,作出与四边形的相似的新四边形,使新图形与原图形的相似比为2:1.
 14. 如图,在等腰△ABC中,AB=AC,点D是AC边上一定点.请用尺规作图法在BC上求作一点P,使得△ABC∽△PCD.(保留作图痕迹,不写作法)
14. 如图,在等腰△ABC中,AB=AC,点D是AC边上一定点.请用尺规作图法在BC上求作一点P,使得△ABC∽△PCD.(保留作图痕迹,不写作法)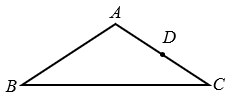 15. 如图,每个正方形都是边长为1个单位长度的正方形,△ABC与△A1B1C1是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
15. 如图,每个正方形都是边长为1个单位长度的正方形,△ABC与△A1B1C1是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.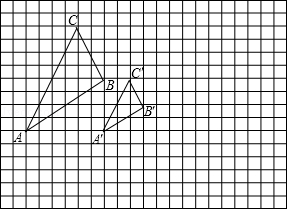 (1)、请在方格中确定位似中心O的位置,并以O为坐标原点,以网格线所在的直线为坐标轴建立平面直角坐标系.(2)、△ABC与△A1B1C1的位似比 .(3)、在图中作出△ABC关于原点O成中心对称的图形△A2B2C2 .16. 如图(1),格点△ABC(顶点在小正方形的顶点处的三角形称为格点三角形) ,请在图(2)、(3)、(4)中的6×6的网格中各画一个互不全等的格点三角形,使它们都和△ABC相似。要求:①其中有一个相似比为 ;②其中有一个面积为5.
(1)、请在方格中确定位似中心O的位置,并以O为坐标原点,以网格线所在的直线为坐标轴建立平面直角坐标系.(2)、△ABC与△A1B1C1的位似比 .(3)、在图中作出△ABC关于原点O成中心对称的图形△A2B2C2 .16. 如图(1),格点△ABC(顶点在小正方形的顶点处的三角形称为格点三角形) ,请在图(2)、(3)、(4)中的6×6的网格中各画一个互不全等的格点三角形,使它们都和△ABC相似。要求:①其中有一个相似比为 ;②其中有一个面积为5.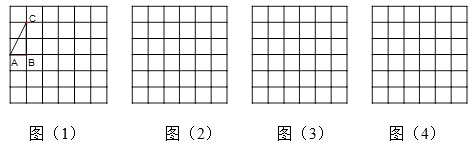 17. 以下各图均是由边长为1的小正方形组成的网格,图中的点A、B、C、D均在格点上.
17. 以下各图均是由边长为1的小正方形组成的网格,图中的点A、B、C、D均在格点上. (1)、在图①中,.(2)、利用网格和无刻度的直尺作图,保留痕迹,不写作法.
(1)、在图①中,.(2)、利用网格和无刻度的直尺作图,保留痕迹,不写作法.①如图②,在上找一点P,使.
②如图③,在上找一点P,使.
18. 如图,在8×8的正方形网格中,已知的顶点都在格点上,请在所给网格中按要求画出图形. (1)、在图1中,将绕着点C顺时针方向旋转得到(点A,B的对应点分别为 , ),并画出.(2)、在图2中,以点C为位似中心,作的位似图形,并使边长放大到原来的2倍,请画出的位似图形.19. 放缩尺是一种绘图工具,它能把图形放大或缩小.
(1)、在图1中,将绕着点C顺时针方向旋转得到(点A,B的对应点分别为 , ),并画出.(2)、在图2中,以点C为位似中心,作的位似图形,并使边长放大到原来的2倍,请画出的位似图形.19. 放缩尺是一种绘图工具,它能把图形放大或缩小.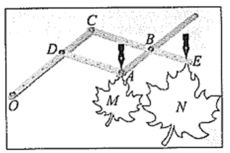
制作:把钻有若干等距小孔的四根直尺用螺栓分别在点A,B,C,D处连接起来,使得直尺可以绕着这些点转动,O为固定点, , , 在点A,E处分别装上画笔.
画图:现有一图形M,画图时固定点O,控制点A处的笔尖沿图形M的轮廓线移动,此时点E处的画笔便画出了将图形M放大后的图形N.
原理:
连接 , , 可证得以下结论:
①和为等腰三角形,则 , (180°-∠ ▲ );
②四边形为平行四边形(理由是 ▲ );
③ , 于是可得O,A,E三点在一条直线上;
④当时,图形N是以点O为位似中心,把图形M放大为原来的 ▲ 倍得到的.