安徽省合肥市瑶海区等4地2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式为最简二次根式的是（　　）

A、 $\sqrt{\frac{1}{3}}$ B、 $\sqrt{0.5}$ C、 $\sqrt{6}$ D、 $\sqrt{16}$

查看试题解析
2. 在下列长度的各组线段中，能组成直角三角形的是（　　）

A、4，5，6 B、5，6，7 C、5，11，12 D、5，12，13

查看试题解析
3. 下列方程中，一定为一元二次方程的是（　　）

A、 $x + 3 y = 4$ B、 $5 y = 5 y^{2}$ C、 $4 x - 4 = 0$ D、 $a x^{2} - x = 1$

查看试题解析
4. 将一元二次方程 $x^{2} - 4 x + 1 = 0$ 配方后得到的结果是（　　）

A、 ${(x - 2)}^{2} - 3 = 0$ B、 ${(x + 2)}^{2} - 3 = 0$ C、 ${(x - 2)}^{2} + 3 = 0$ D、 ${(x + 2)}^{2} + 3 = 0$

查看试题解析
5. 勾股定理是中国几何的根源，中华数学的精髓，诸如开方术、方程术、天元术等技艺的诞生与发展，寻根探源，都与勾股定理有着密切关系．如图， $△ A B C$ 中， $∠ A B C = 90 °$ ，若 $A B = 2$ ， $B C = 3$ ，则正方形 $A C D E$ 的面积为（　　）

A、4 B、 $\sqrt{13}$ C、13 D、16

查看试题解析
6. 已知一组数据：2，1，3，2，2，这组数据的方差是（　　）

A、 $0.4$ B、 $0.6$ C、2 D、3

查看试题解析
7. 下列叙述错误的是（）

A、平行四边形的对角线互相平分 B、矩形的对角线相等 C、对角线互相平分的四边形是平行四边形 D、对角线相等的四边形是矩形

查看试题解析
8. 某商店将进货价格为20元的商品按单价36元售出时，能卖出200个．已知该商品单价每上涨1元，其销售量就减少5个．设这种商品的售价上涨 $x$ 元时，获得的利润为1200元，则下列关系式正确的是（　　）

A、 $(x + 16) (200 - 5 x) = 1200$ B、 $(x + 16) (200 + 5 x) = 1200$ C、 $(x - 16) (200 + 5 x) = 1200$ D、 $(x - 16) (200 - 5 x) = 1200$

查看试题解析
9. 已知菱形 $A B C D$ 的对角线 $A C 、 B D$ 的长度恰为方程的 $x^{2} - 14 x + 48 = 0$ 两个实数根，则菱形 $A B C D$ 的周长为（　　）

A、12 B、16 C、20 D、24

查看试题解析
10. 如图，矩形 $A B C D$ 中，E为 $B C$ 边的中点，沿 $D E$ 对折矩形，使点C落在 $C^{'}$ 处，折痕为 $D E$ ，延长 $D C^{'}$ 交 $A B$ 于点F，连接 $B C^{'}$ 并延长交 $A D$ 于点G，连接 $C C^{'}$ ．给出以下结论：①四边形 $B E D G$ 为平行四边形；② $∠ E C^{'} C = ∠ B C^{'} F$ ；③ $G C^{'} = G D$ ；④ $C^{'}$ 为 $B G$ 的中点．其中正确结论的个数是（　　）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{x - 4}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 若一元二次方程 $x^{2} - 2 x + 2 a = 0$ 有两个相等的实数根，则a的值为

查看试题解析
13. 如图，一个正五边形和一个正方形各有一边在直线 $l$ 上，且只有一个公共顶点A，则 $∠ B A C$ 的大小为度．

查看试题解析
14. 如图，A、B、C分别为数轴上的三点，且 $A B = B C$ ，若点B对应的实数为1，点 $C$ 对应的实数为 $\sqrt{3}$ ，则点A对应的实数为．

查看试题解析
15. 如图，AD为 $△ A B C$ 的外角平分线， $C D ⊥ A D$ 于点D，M为BC边的中点，若 $B C = M D = 6$ ，则 $△ A B C$ 的周长为．

查看试题解析

三、解答题

16. 计算： ${(- \sqrt{6})}^{2} - 3 \sqrt{2} \times \sqrt{18}$

查看试题解析
17. 解方程： $x^{2} + 3 x - 1 = 0$

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = A C$ ，点D为形外一点，且 $A B ∥ C D$ ， $A B = 2 C D$ ， M为 $A B$ 的中点，请仅用无刻度的直尺分别按下列要求画图．（保留画图痕迹，不需要证明）

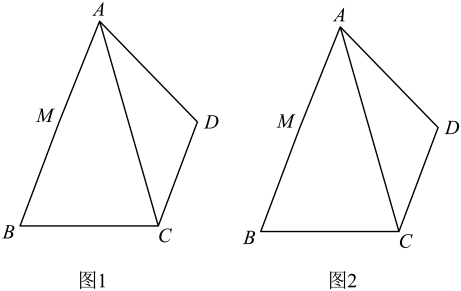(1)、在图1中，画出 $△ A B C$ 的 $A C$ 边上的中线 $B E$ ；

(2)、在图2中，先画出 $A C$ 边的中点E，再画出 $△ A B C$ 的 $B C$ 边上的高 $A H$ ．

查看试题解析
19. 某工厂利用空地新建一个长方形电动车棚，其中一面靠院墙，如图1，这堵墙的长度为10米．已知现有的木板材料（图中细线部分）可新建围墙26米，同时在与院墙平行的一面开一个2米宽的门，设该长方形电动车棚与院墙垂直的一边长为 $a$ 米

(1)、求与墙平行的一边长为多少米？（用含 $a$ 的代数式表示）

(2)、当 $a = 10$ 时，为了方便职工通行，施工单位决定在车棚内修建几条等宽的小路（如图2中内部阴影区域），使得停放电动车的空白面积为54平方米，那么小路的宽度是多少米？

查看试题解析
20. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $C D$ 为 $A B$ 边上的中线，过C点作 $C E ∥ A D$ ，连接 $A E$ ，且 $C E = A E$ ．

(1)、求证：四边形 $A D C E$ 为菱形

(2)、若 $A E = 5$ ， $A C = 6$ ，求四边形 $A B C E$ 的面积

查看试题解析

21. 为深入学习贯彻习近平法治思想，推动青少年宪法学习宣传教育走深走实，教育部组织开展全国学生“学宪法讲宪法”系列活动．某校积极响应教育部的号召，开展了宪法知识普及测评，现分别从七、八年级中各随机抽取了8名学生的成绩（满分10分）进行整理与分析，信息如下：

收集信息：

七年级：8，10，7，6，6，7，10，6；

八年级：9，10，6，10，10，6，9，8．

整理信息：

	平均数	中位数	众数
七年级	7.5	$a$	6
八年级	$b$	9	$c$

(1)、填空：

a =

，

b =

，

c =

．

(2)、若该校八年级共有1000名学生参加此次测评，请估计该校八年级学生中优秀（大于等于9分）的人数．

查看试题解析

22. 如图，正方形 $A B C D$ 中，E为 $C D$ 边上一点， $C F ⊥ A E$ 交 $A E$ 的延长线于点F， $D G ⊥ D F$ 交 $A E$ 于点G．

(1)、求证： $△ D A G ≌ △ D C F$ ；

(2)、若E为 $C D$ 的中点， $F C = 2$ ，求正方形 $A B C D$ 的面积，

查看试题解析

四、填空题

23. 若实数a，b满足 $a - 2 a b + 2 a b^{2} + 4 = 0$ ，则a的取值范围是．

查看试题解析