安徽省宿州市泗县2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
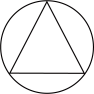 B、
B、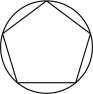 C、
C、 D、
D、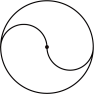 2. 如果 , 那么下列各式中一定正确的是( )A、 B、 C、 D、3. 在平行四边形中, , , 对角线的取值范围是( )A、 B、 C、 D、4. 若分式中的、的值同时扩大到原来的10倍,则分式的值( )A、是原来的30倍 B、是原来的10倍 C、是原来的倍 D、不变5. 不等式组的每个不等式解集在数轴上表示正确的是( )A、
2. 如果 , 那么下列各式中一定正确的是( )A、 B、 C、 D、3. 在平行四边形中, , , 对角线的取值范围是( )A、 B、 C、 D、4. 若分式中的、的值同时扩大到原来的10倍,则分式的值( )A、是原来的30倍 B、是原来的10倍 C、是原来的倍 D、不变5. 不等式组的每个不等式解集在数轴上表示正确的是( )A、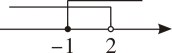 B、
B、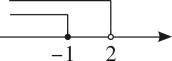 C、
C、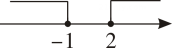 D、
D、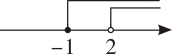 6. 如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )
6. 如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )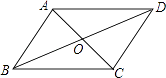 A、AB=CD B、AD∥BC C、OA=OC D、AD=BC7. 如图,在中,的垂直平分线分别交 , 于点D,E.若的周长为 , , 则的周长为( )
A、AB=CD B、AD∥BC C、OA=OC D、AD=BC7. 如图,在中,的垂直平分线分别交 , 于点D,E.若的周长为 , , 则的周长为( ) A、14 B、16 C、18 D、208. 如图,直线经过两点,且与直线交于点 , 则不等式的解集为( )
A、14 B、16 C、18 D、208. 如图,直线经过两点,且与直线交于点 , 则不等式的解集为( )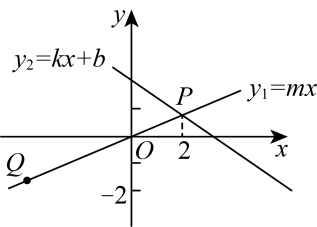 A、 B、 C、 D、9. 如图,、在平行四边形的对角线上, , , , 则的大小为( )
A、 B、 C、 D、9. 如图,、在平行四边形的对角线上, , , , 则的大小为( ) A、 B、 C、 D、10. 数学家莫伦在年发现了世界上第一个完美长方形(如图),即它恰好能被分割成个大小不同的正方形,从这以后人们开始热衷图形完美分割的研究,平行四边形被分割成个小正三角形(如图2),已知中间最小的两个正三角形和边长均为 , 平行四边形的周长为( )
A、 B、 C、 D、10. 数学家莫伦在年发现了世界上第一个完美长方形(如图),即它恰好能被分割成个大小不同的正方形,从这以后人们开始热衷图形完美分割的研究,平行四边形被分割成个小正三角形(如图2),已知中间最小的两个正三角形和边长均为 , 平行四边形的周长为( )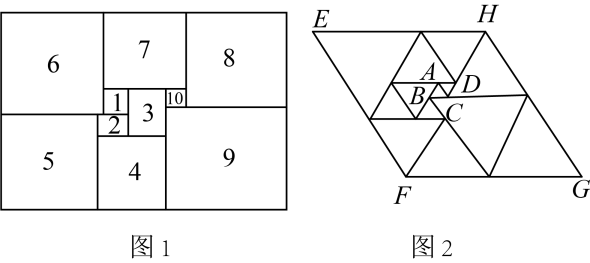 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
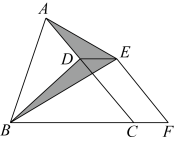
11. 若分式的值为0,则x的值为 .12. 已知一个多边形的内角和是外角和的2倍,则这个多边形为边形.13. 分解因式: .14. 若三角形三个内角的度数之比为 , 最短的边长是 , 则其最长的边的长是 .15. 已知关于的不等式组有且仅有三个整数解,则的取值范围是 .16. 如果关于x的方程 的解为负数,则m的取值范围是.17. 已知 , 求分式的值为 .18. 如图,已知的面积为 , 点在线段上,点在线段的延长线上,且 , 四边形是平行四边形,则图中阴影部分的面积为 .
三、解答题
-
19. 先化简,再求值: . 其中且为整数,请你从中选取一个喜欢的数代入求值.20. 如图,在平行四边形中,对角线交于点 , 过点任作直线分别交、于点E、F.
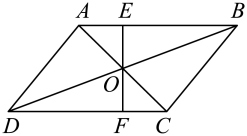 (1)、求证:;(2)、若 , , , 求四边形的周长.21. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,的三个顶点 , , 均在格点上.
(1)、求证:;(2)、若 , , , 求四边形的周长.21. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,的三个顶点 , , 均在格点上. (1)、画出将向左平移个单位长度得到的;(2)、画出绕点顺时针旋转后得到的 , 并写出的坐标.22. 某超市用4000元购进某种菌菇销售,由于销售状况良好,超市又调拨10000元资金购进该种菌菇,但这次每千克的进价比第一次的进价提高了5元,购进菌菇数量是第一次的2倍.(1)、该种菌菇的第一次进价是每千克多少元?(2)、如果这两批菌菇每千克售价相同,且全部售完后总利润不低于 , 那么每千克菌菇的售价至少是多少元?23. 把代数式通过配方等手段,得到完全平方式,再运用完全平方式的非负性来增加题目的已知条件,这种解题方法叫做配方法.配方法在代数式求值、解方程、最值问题等都有着广泛的应用.
(1)、画出将向左平移个单位长度得到的;(2)、画出绕点顺时针旋转后得到的 , 并写出的坐标.22. 某超市用4000元购进某种菌菇销售,由于销售状况良好,超市又调拨10000元资金购进该种菌菇,但这次每千克的进价比第一次的进价提高了5元,购进菌菇数量是第一次的2倍.(1)、该种菌菇的第一次进价是每千克多少元?(2)、如果这两批菌菇每千克售价相同,且全部售完后总利润不低于 , 那么每千克菌菇的售价至少是多少元?23. 把代数式通过配方等手段,得到完全平方式,再运用完全平方式的非负性来增加题目的已知条件,这种解题方法叫做配方法.配方法在代数式求值、解方程、最值问题等都有着广泛的应用.例如:①用配方法分解因式:
原式
②利用配方法求最小值:求最小值.
解: , 因为不论取何值,总是非负数,即 , 所以 , 所以当时,有最小值,最小值是 .
根据上述材料,解答下列问题:
(1)、填空:;(2)、将变形为的形式,并求出的最小值;(3)、若 , , 其中为任意实数,试比较与的大小,并说明理由.