上海市宝山区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 一次函数 的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列方程有实数根的是( )A、 B、 C、 D、3. 如图,矩形的对角线和交于点O,下列选项中错误的是( )
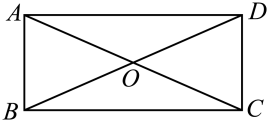 A、 B、 C、 D、4. 上海市16个区共约1326条健身步进和绿道,甲、乙两人沿着总长度为9千米的“健身步道”行走,甲的速度是乙的1.5倍,甲比乙提前15分钟走完全程,如果设乙的速度为x千米/时,那么下列方程中正确的是( )A、 B、 C、 D、5. 北京时间2023年5月10日,搭载天舟六号货运飞船的长征七号运载火箭发射成功.某校六年级航天兴趣小组共16人,随机调查了六年级的部分学生对中国航天事业的关注程度,发现很多同学心中都有一个伟大的航天梦,那么“在该校六年级所有学生中随机抽取一人参加中国航天主题分享活动,抽中的学生一定来自航天兴趣小组”是( )A、随机事件 B、确定事件 C、必然事件 D、不可能事件6. 如图,中,已知点分别是的中点,那么下列判断中错误的是( )
A、 B、 C、 D、4. 上海市16个区共约1326条健身步进和绿道,甲、乙两人沿着总长度为9千米的“健身步道”行走,甲的速度是乙的1.5倍,甲比乙提前15分钟走完全程,如果设乙的速度为x千米/时,那么下列方程中正确的是( )A、 B、 C、 D、5. 北京时间2023年5月10日,搭载天舟六号货运飞船的长征七号运载火箭发射成功.某校六年级航天兴趣小组共16人,随机调查了六年级的部分学生对中国航天事业的关注程度,发现很多同学心中都有一个伟大的航天梦,那么“在该校六年级所有学生中随机抽取一人参加中国航天主题分享活动,抽中的学生一定来自航天兴趣小组”是( )A、随机事件 B、确定事件 C、必然事件 D、不可能事件6. 如图,中,已知点分别是的中点,那么下列判断中错误的是( )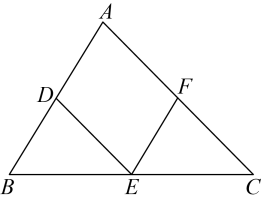 A、四边形是平行四边形 B、如果 , 那么四边形是菱形 C、如果 , 那么四边形是矩形 D、如果是等腰直角三角形,那么四边形是正方形
A、四边形是平行四边形 B、如果 , 那么四边形是菱形 C、如果 , 那么四边形是矩形 D、如果是等腰直角三角形,那么四边形是正方形二、填空题
-
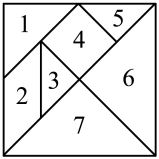
7. .8. 方程的根是 .9. 方程的根是 .10. 已知直线与直线相交于点 , 那么 .11. 已知点都在一次函数的图象上,那么m与n的大小关系是 .12. 已知点A是直线在第一象限内的一点,且它到两坐标轴的距离相等,那么点A的坐标是 .13. 如果一个二十边形的每个内角都相等,那么它的每个外角的度数是 .14. 顺次连接矩形四边中点所得的四边形是 .15. 七巧板游戏是中国人的智慧结晶.如图,七巧板是由个几何图形组成的正方形,其中、、、、是等腰直角三角形,是正方形,是平行四边形。一只蚂蚁在七巧板上随机停留,刚巧停在号板区域的概率是 .
 16. 如图,已知梯形 , , , 那么 .
16. 如图,已知梯形 , , , 那么 .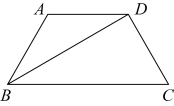 17. 已知矩形 , 把矩形沿直线翻折,点A落在点E处,如果的长度等于该矩形的一条边长,那么 .
17. 已知矩形 , 把矩形沿直线翻折,点A落在点E处,如果的长度等于该矩形的一条边长,那么 .三、解答题
-
18. 解方程: .19. 解方程组∶ .20. 如图,已知点E在梯形的边上.
 (1)、计算;(2)、设 , , .
(1)、计算;(2)、设 , , .①试用向量 , 、表示向量=;
②在图中求作: . (不要求写出作法,只需写出结论即可)
21. 元朝朱世杰的《算学启蒙》一书记载了一个数学问题:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之.”它的大意是∶“良马每天行里,劣马每天行里,劣马先行天,良马需要多少天才能追上劣马?”如图,是良马与驽马行走路程(单位∶里)关于行走时间(单位∶日)的函数图象. (1)、射线记为 , 射线记为 , 那么良马行走路程关于行走时间的函数图象是;(填或)(2)、两图象交点的坐标是;(3)、求良马行走路程关于行走时间的函数解析式.22. 如图,在矩形中,对角线、相交于点 , 为的中点,连接并延长至点 , 使 , 连接、 .
(1)、射线记为 , 射线记为 , 那么良马行走路程关于行走时间的函数图象是;(填或)(2)、两图象交点的坐标是;(3)、求良马行走路程关于行走时间的函数解析式.22. 如图,在矩形中,对角线、相交于点 , 为的中点,连接并延长至点 , 使 , 连接、 .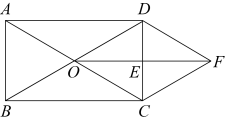 (1)、求证:四边形是菱形;(2)、已知 , , 求的长.23. 如图,点A的坐标为 , 点B、C在x轴上,且轴, , 直线与y轴交于点D,E是直线上的一个动点.
(1)、求证:四边形是菱形;(2)、已知 , , 求的长.23. 如图,点A的坐标为 , 点B、C在x轴上,且轴, , 直线与y轴交于点D,E是直线上的一个动点.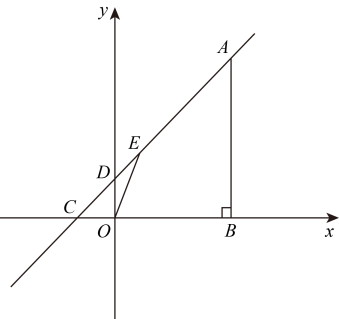 (1)、求直线的表达式;(2)、当点E在线段上,联结 , 如果的面积是面积的一半,求点E的坐标;(3)、设点F是平面内一点,如果以A、E、B、F为顶点的四边形为正方形,试求出点F的坐标.24. 平行四边形中,E是边上的动点,过点E作 , 垂足为点G,F是边的中点,连接 .
(1)、求直线的表达式;(2)、当点E在线段上,联结 , 如果的面积是面积的一半,求点E的坐标;(3)、设点F是平面内一点,如果以A、E、B、F为顶点的四边形为正方形,试求出点F的坐标.24. 平行四边形中,E是边上的动点,过点E作 , 垂足为点G,F是边的中点,连接 .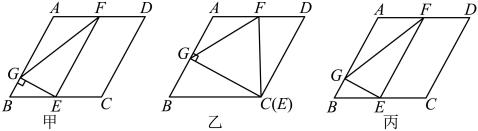 (1)、如图甲,当E是边的中点时,如果四边形的面积为10,求的面积;(2)、如图乙,点E移动至点C处,试判断形状,并说明理由;(3)、如图丙,如果 , , 设 , , 求y与x的函数关系式,并写出定义域.
(1)、如图甲,当E是边的中点时,如果四边形的面积为10,求的面积;(2)、如图乙,点E移动至点C处,试判断形状,并说明理由;(3)、如图丙,如果 , , 设 , , 求y与x的函数关系式,并写出定义域.