上海市普陀区2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列函数中，y是x的一次函数的是（）

A、 $y = x^{2} - 5$ B、 $y = 3$ C、 $y = k x + b$ D、 $y = x - 1$

查看试题解析
2. 一次函数 $y = - 2 x + 1$ 的图象经过哪几个象限（）

A、一、二、三象限 B、一、二、四象限 C、一、三、四象限 D、二、三、四象限

查看试题解析
3. 下列方程中，有实数根的是（）

A、 $x^{2} - x + 4 = 0$ B、 $\sqrt{x - 3} + 2 = 0$ C、 $\sqrt{x + 2} = - x$ D、 $\frac{x}{x^{2} - 1} = \frac{1}{x^{2} - 1}$

查看试题解析
4. 下列事件中，属于必然事件的是（）

A、在十进制中， $1 + 1 = 2$ B、在实数中任取一个数，这个数的平方小于0 C、任意画一个三角形是等腰三角形 D、掷一枚骰子，点数为4的一面朝上

查看试题解析
5. 如果点C是线段 $A B$ 的中点，那么下列结论中错误的是（）

A、 $\vec{A C}$ 与 $\vec{B C}$ 是相反向量 B、 $\vec{C A}$ 与 $\vec{B C}$ 是相等向量 C、 $\vec{A C}$ 与 $\vec{A B}$ 是平行向量 D、 $\vec{A C} + \vec{B C} = 0$

查看试题解析
6. 已知四边形 $A B C D$ 中， $A B / / C D ， A C = B D$ ，下列判断中的正确的是（）

A、如果 $B C = A D$ ，那么四边形 $A B C D$ 是等腰梯形 B、如果 $A D / / B C$ ，那么四边形 $A B C D$ 是菱形 C、如果AC平分BD，那么四边形 $A B C D$ 是矩形 D、如果 $A C ⊥ B D$ ，那么四边形 $A B C D$ 是正方形

查看试题解析

二、填空题

7. 方程 $x^{3} - 27 = 0$ 的解是．

查看试题解析
8. 已知一次函数 $f (x) = \frac{1}{2} x + 3$ ，那么 $f (- 4) =$ ．

查看试题解析
9. 如图，直线 $y = k x + b$ 经过 $(- 2 ， 0)$ ， $(0 ， 1)$ 两点，则不等式 $k x + b > 0$ 的解集为；

查看试题解析
10. 用换元法解方程 $\frac{3 x}{x^{2} - 1} - \frac{x^{2} - 1}{x} = 2$ ，如果设 $y = \frac{x}{x^{2} - 1}$ ，那么原方程可以化为关于y的整式方程为．

查看试题解析
11. 已知一个正多边形的一个外角为 $36 °$ ，则这个正多边形的边数是．

查看试题解析
12. 从1，2，4这三个数中任取两个数组成没有重复数字的两位数，那么组成的两位数是奇数的概率为．

查看试题解析
13. 书香相伴，香满校园，某校学生9月份借阅图书500本，11月份借阅图书845本，如果每月借阅图书数量的增长率相同，设这个增长率为x，那么根据题意可列方程为．

查看试题解析
14. 用一根20cm长的绳子围成一个矩形，使其相邻两边的长度比为 $3 ： 2$ ，那么这个矩形的面积为 $c m^{2}$ ．

查看试题解析
15. 在正方形ABCD中，E是对角线AC上一点，且AE=AB，则∠EBC的度数是．

查看试题解析
16. 如图，在平行四边形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点O．设 $\vec{O A} = \vec{a}$ ， $\vec{D O} = \vec{b}$ ，那么向量 $\vec{D C}$ 用向量 $\vec{a}$ 、 $\vec{b}$ 表示为．

查看试题解析
17. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $A D$ 是 $△ A B C$ 的中线，点 $E$ ， $F$ 分别是 $A D$ ， $A C$ 的中点，连接 $E F$ ，若 $E F = 3$ ，则 $A D$ 的长为．

查看试题解析
18. 如图，平行四边形 $A B C D$ 中， $B C = 4 ， ∠ B = 30 °$ ， $∠ A C B = 45 °$ ，将 $△ A B C$ 沿着 $A C$ 翻折，点B的对应点为点E，连接 $D E$ ，那么线段 $D E =$ ．

查看试题解析

三、解答题

19. 解方程： $\sqrt{5 - x} - 1 = x$ ．

查看试题解析
20. 解方程组： ${\begin{array}{l} 2 x - y = 6 \\ x^{2} - x y - 2 y^{2} = 0 \end{array}$

查看试题解析
21. 甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案．
甲公司方案：每月的养护费用y（元）与绿化面积x（平方米）是一次函数关系，如图所示．
乙公司方案：绿化面积不超过1000平方米时，每月收取费用5500 元；绿化面积超过1000平方米时，每月在收取5500元的基础上，超过部分每平方米收取4元．

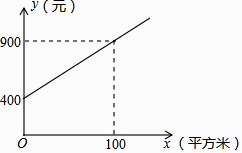(1)、求如图所示的y与x的函数解析式：（不要求写出定义域）；

(2)、如果某学校目前的绿化面积是1200平方米，试通过计算说明：选择哪家公司的服务，每月的绿化养护费用较少．

查看试题解析
22. A、B两地相距360千米，一辆汽车准备从A地开往B地，但由于任务紧急，现在实际行驶的速度每小时比原计划快20千米，所以提前3小时到达B地．求汽车原计划的速度．

查看试题解析
23. 已知：如图，在四边形 $A B C D$ 中， $A D ∥ B C$ ，对角线 $A C$ 、 $B D$ 相交于点O， $B D$ 平分 $∠ A B C$ ，过点D作 $D F ∥ A B$ 分别交 $A C$ 、 $B C$ 于点E、F．

(1)、求证：四边形 $A B F D$ 是菱形；

(2)、如果 $∠ B A D = 2 ∠ A D C$ ，求证： $A C = D F$ ．

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，直线 $y = x + 4$ 与y轴交于点A，且与直线 $C D$ 交于点 $B (m ， 2)$ ，直线 $C D$ 与x轴、y轴分别交于点D、C，点C的坐标为 $(0 ， - 2)$ ．

(1)、求 $△ A B C$ 的面积；

(2)、过点A作 $B C$ 的平行线交x轴于点E，
①求点E的坐标；

②点P是直线 $A B$ 上一动点且在x轴的上方，Q为直角坐标平面内一点，如果以点D，E，P，Q为顶点，且以 $D E$ 为边的平行四边形的面积等于 $△ A B C$ 的面积，请求出点P的坐标，并直接写出点Q的坐标．

查看试题解析
25. 在梯形 $A B C D$ 中， $A D ∥ B C$ ， $A B ⊥ B C$ ， $A D = 4 ， B C = 6$ ， $D C = 2 \sqrt{10}$ ，点E是射线 $A B$ 上一点（不与点A、B重合），联结 $D E$ ，过点E作 $E F ⊥ D E$ 交射线 $C B$ 于点F，联结 $D F$ ．设 $A E = x ， F C = y$ ．

(1)、求 $A B$ 的长；

(2)、如图，当点E在线段 $A B$ 上时，求y与x之间的函数解析式，并写出自变量x的取值范围；

(3)、如果 $△ D F C$ 是以 $D F$ 为腰的等腰三角形，求 $A E$ 的长．

查看试题解析