上海市青浦区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 直线的图象经过( )A、第一、二、三象限 B、第一、二、四象限 C、第一、三、四象限 D、第二、三、四象限2. 下列方程中,有实数根的方程是( )A、 B、 C、 D、3. 下列事件中是必然事件的是( )A、投掷一枚质地均匀的硬币10次,正面朝上的次数为5次 B、任取一个实数,它的平方大于零 C、两位同学玩“石头、剪刀、布”的游戏,一个回合定出胜负 D、某兴趣小组由13名同学组成,其中至少有两名同学的生日在同一个月4. 已知平行四边形 , 下列说法中错误的是( )A、 B、 C、 D、5. 如图,函数的图象与y轴、x轴分别相交于点和点 , 则关于x的不等式的解集为( )
 A、 B、 C、 D、6. 已知平行四边形的对角线相交于点O.下列补充条件中,能判定这个平行四边形是菱形的是( )A、 B、 C、 D、
A、 B、 C、 D、6. 已知平行四边形的对角线相交于点O.下列补充条件中,能判定这个平行四边形是菱形的是( )A、 B、 C、 D、二、填空题
-
7. 一次函数 的截距为 .8. 函数的定义域为 .9. 如果关于的方程有实数解,那么的取值范围是.10. 用换元法解方程 , 若设 , 则原方程可化为关于y的整式方程是 .11. 将直线 向右平移2个单位,得到的直线解析式为 .12. 一辆汽车,新车购买价为25万元,第一年使用后折旧20%,以后该车的年折旧率有所变化,但它在第二、三年的年折旧率相同.已知在第三年年末,这辆车折旧后价值14.45万元,设这辆车在第二、三年的年折旧率为a,则可列方程为 .13. 在平行四边形中, , , 则 .14. 若一个边形的每个内角都为 , 那么边数为 .15. 若菱形的边长为10,一条对角线长为12,则另一条对角线长为 .16. 从① , ② , ③ , ④四个关系中,任选两个作为条件,那么选到能够判定四边形是平行四边形的概率是 .17. 在等腰梯形中, , , , , 则该等腰梯形的高的长度是 .18. 如图,在矩形中, , , 点E为边中点,将沿翻折,点A落到点F处,延长交边于点G,则线段的长度为 .
三、解答题
-
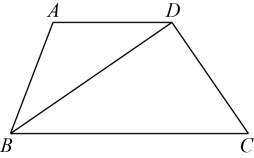
19. 解分式方程:20. 解方程组: .21. 如图,在菱形中,点E为边中点,连接 , .
 (1)、求的度数;(2)、连接 , 如果 , 求菱形的面积.22. 已知甲、乙两车分别从A、B两地同时出发,沿同一条公路相向而行,甲车先以75千米/时的速度匀速行驶150千米后与乙车相遇,再以另一速度继续匀速行驶3小时到达B地;乙车匀速行驶至A地,两车到达各自的目的地后停止.甲、乙两车各自距A地的路程y(km)与行驶时间x(h)之间的函数关系如图所示.
(1)、求的度数;(2)、连接 , 如果 , 求菱形的面积.22. 已知甲、乙两车分别从A、B两地同时出发,沿同一条公路相向而行,甲车先以75千米/时的速度匀速行驶150千米后与乙车相遇,再以另一速度继续匀速行驶3小时到达B地;乙车匀速行驶至A地,两车到达各自的目的地后停止.甲、乙两车各自距A地的路程y(km)与行驶时间x(h)之间的函数关系如图所示.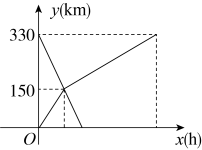 (1)、求两车相遇后,甲车距A地的路程y与行驶时间x之间的函数关系式;(2)、当乙车到达A地时,求甲车距A地的路程.23. 如图,在三角形中, , 分别是与它的邻补角的平分线,于点E.
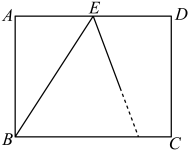
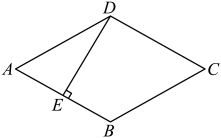
(1)、求两车相遇后,甲车距A地的路程y与行驶时间x之间的函数关系式;(2)、当乙车到达A地时,求甲车距A地的路程.23. 如图,在三角形中, , 分别是与它的邻补角的平分线,于点E.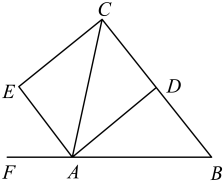 (1)、求证:四边形是矩形;(2)、连接交AC于点O,若 , 求证:四边形是正方形.
(1)、求证:四边形是矩形;(2)、连接交AC于点O,若 , 求证:四边形是正方形.