上海市浦东新区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 下列函数中,是一次函数的是( )A、 B、 C、 D、2. 用换元法解方程时,下列换元方法中最合适的换元方法是 ( )A、设 B、设 C、 D、3. 方程的解是( )A、 B、 C、 D、4. 下列事件是必然事件的是( )A、两个不相同无理数的和是无理数 B、两个不相同无理数的差是无理数 C、两个不相同无理数的积是无理数 D、两个不相同无理数的商是无理数5. 如果O是正方形对角线 , 的交点,那么向量、、 , 是( )A、相等向量 B、相反向量 C、平行向量 D、模相等的向量6. 已知四边形 , , 、是它的两条对角线,下列条件中,不能判定四边形是菱形的是( )A、 B、 C、 D、
二、填空题
-
7. 如果将直线向上平移1个单位,那么所得新直线的表达式是 .8. 直线 的截距是 .9. 关于x的方程的解是 .10. 方程的解是 .11. 写出二元二次方程的一对整数解是 .12. 有一个两位数,如果个位上的数比十位上的数大1,并其十位上的数的平方比个位上的数也大1,那么这个两位数是 .13. 四张完全相同的卡片上,分别画有平行四边形、矩形、等腰梯形和等腰三角形,如果从中任意抽取1张卡片,抽中的卡片上所画图形恰好是中心对称图形的概率是 .14. 一个多边形的每一个外角都等于45°,则这个多边形的内角和为15. 如图,已知梯形 , , 点在底边上, . 如果设 , , 那么 . (用向量 , 的式于表示)
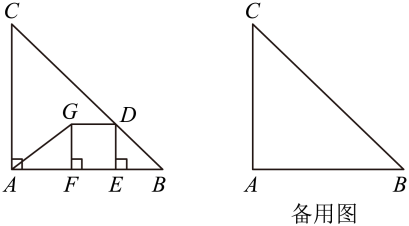
 16. 如果菱形的面积是24,较短的对角线长为6.那么这个菱形的边长是 .17. 如图,被平行于边的直线l分成梯形和小 , 当为直角三角形,且时,我们叫梯形是“余角梯形”.如果一个“余角梯形”较短底边长5,两腰长分别是3和4,那么它的中位线长是 .
16. 如果菱形的面积是24,较短的对角线长为6.那么这个菱形的边长是 .17. 如图,被平行于边的直线l分成梯形和小 , 当为直角三角形,且时,我们叫梯形是“余角梯形”.如果一个“余角梯形”较短底边长5,两腰长分别是3和4,那么它的中位线长是 . 18. 如图,在中, , , 点M在边上,过点M作 , 垂足为点M,交边于点N,将沿直线翻折,点A、C分别与点D、E对应,如果四边形是平行四边形,那么的长是 .
18. 如图,在中, , , 点M在边上,过点M作 , 垂足为点M,交边于点N,将沿直线翻折,点A、C分别与点D、E对应,如果四边形是平行四边形,那么的长是 .
三、解答题
-
19. 解分式方程:+1= .20. 某班六一节联欢会设计了即兴表演节目的摸球游戏,用一个不透明的盒子,里面装有四个分别标有数字1、2、3、4的乒乓球,这些球除数字外,其它完全相同.游戏规则是:参加联欢会的所有同学从盒子中随机一次摸出两个球(每位同学只能摸一次),如果两球上的数字之和是偶数就给大家即兴表演一个节;否则,下个同学接着做摸球游戏依次进行.(1)、用树状图表示所有等可能的结果;(2)、求参加联欢会的同学表演即兴节目的概率.21. 如图,已知梯形 , , , .
 (1)、求的度数;(2)、过点D作 , 垂足为点E,连接 , 如果 , 求的长.22. 我们知道,海拔高度每上升1千米,温度下降 , 某时刻,上海地面温度为 , 设高出地面千米处的温度为 .(1)、写出与之间的函数关系式,并写出函数定义域;(2)、有一架飞机飞过浦东上空,如果机舱内仪表显示飞机外面的温度为 , 求此刻飞机离地面的高度为多少千米?23. 已知,如图,中, , 是边的延长线上一点,过作 , 交的延长线于点 , .
(1)、求的度数;(2)、过点D作 , 垂足为点E,连接 , 如果 , 求的长.22. 我们知道,海拔高度每上升1千米,温度下降 , 某时刻,上海地面温度为 , 设高出地面千米处的温度为 .(1)、写出与之间的函数关系式,并写出函数定义域;(2)、有一架飞机飞过浦东上空,如果机舱内仪表显示飞机外面的温度为 , 求此刻飞机离地面的高度为多少千米?23. 已知,如图,中, , 是边的延长线上一点,过作 , 交的延长线于点 , . (1)、求证:四边形是平行四边形;(2)、连接 , 当是的中点时,求证:四边形为矩形.
(1)、求证:四边形是平行四边形;(2)、连接 , 当是的中点时,求证:四边形为矩形.