上海市松江区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 一次函数y=2x-5的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 在下列方程中,有实数根的是( )A、 B、 C、 D、3. 下列等式中不正确的是( )A、 B、 C、 D、4. 解方程时,设 , 则原方程可化为关于的整式方程是( )A、 B、 C、 D、5. 下列各事件中,属于必然事件的是( )A、拋一枚硬币,反面朝上; B、早上出门,在第一个路口遇到绿灯; C、6本书分放在5个抽屉,至少一个抽屉内有2本书. D、在平面内,度量一个三角形的内角度数,内角和为360°6. 乐乐家与学校相距1000米,某天乐乐上学时忘了带了一本书,走了一段时间才想起,于是返回家拿书,然后加快速度赶到学校,图中是乐乐与家的距离y(米)关于时间x(分钟)的函数图象,下列说法错误的是( )
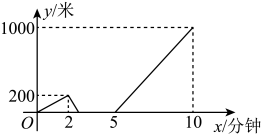 A、乐乐走了200米后返回家拿书 B、乐乐在家停留了3分钟 C、乐乐以每分钟200米的速度加速赶到学校 D、乐乐在第10分钟的时候赶到学校
A、乐乐走了200米后返回家拿书 B、乐乐在家停留了3分钟 C、乐乐以每分钟200米的速度加速赶到学校 D、乐乐在第10分钟的时候赶到学校二、填空题
-
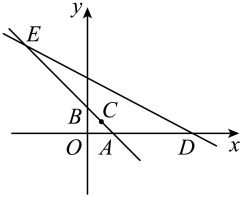
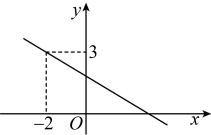
7. 直线 的截距是 .8. 方程的解是 .9. 方程的根是 .10. 关于的方程:的根为 .11. 已知一个多边形的内角和等于900°,则这个多边形的边数是 .12. 布袋里装有3个红球、5个黄球、6个黑球,这些球除颜色外其余都相同,那么从这个布袋里摸出一个黑球的概率为 .13. 平行于直线 , 且与轴交于点的直线表达式是 .14. 如图:点在直线上,则不等式关于的解集是 .
 15. 在四边形ABCD中,已知∠A+∠B=180°,要使四边形ABCD是平行四边形,还需添加一个条件,这个条件可以是 . (只需填写一种情况)
15. 在四边形ABCD中,已知∠A+∠B=180°,要使四边形ABCD是平行四边形,还需添加一个条件,这个条件可以是 . (只需填写一种情况)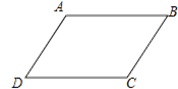 16. 菱形的边长为5,一条对角线长为8,则此菱形的面积是 .17. 如图,在梯形中, , , , , , 那么梯形的周长为cm.
16. 菱形的边长为5,一条对角线长为8,则此菱形的面积是 .17. 如图,在梯形中, , , , , , 那么梯形的周长为cm.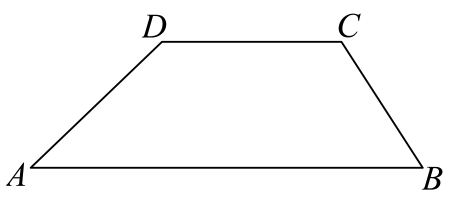 18. 已知:如图,在矩形中, . 点P是边上一点,且 . 连接 , 将四边形沿所在直线翻折,点A、B的对应点分别为点E、F,边与边的交点为点G.则;
18. 已知:如图,在矩形中, . 点P是边上一点,且 . 连接 , 将四边形沿所在直线翻折,点A、B的对应点分别为点E、F,边与边的交点为点G.则;
三、解答题
-
19. 解方程:20. 解方程组:21. 如图,已知在平行四边形中,点E、F分别在边上,且 , , 连接 .
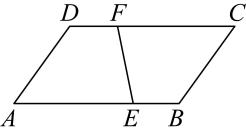 (1)、写出与相等的向量;(2)、填空;(3)、求作: . (保留作图痕迹,不要求写作法,请说明哪个向量是所求作的向量)22. 如图,甲、乙两人到距离A地35千米的B地办事,甲步行先走,乙骑车后走,两人行进的路程和时间的关系如图所示,根据图示提供的信息解答:
(1)、写出与相等的向量;(2)、填空;(3)、求作: . (保留作图痕迹,不要求写作法,请说明哪个向量是所求作的向量)22. 如图,甲、乙两人到距离A地35千米的B地办事,甲步行先走,乙骑车后走,两人行进的路程和时间的关系如图所示,根据图示提供的信息解答: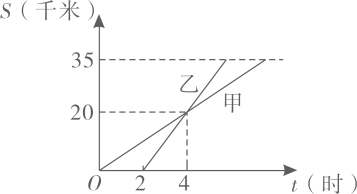 (1)、乙比甲晚 小时出发;乙出发 小时后追上甲;(2)、求乙比甲早几小时到达B地?23. 松江区于4月22日,举办“”上海佘山半程马拉松比赛.主办方打算为参赛选手定制一批护膝,并交由A厂家完成.已知A厂家要在规定的天数内生产3600对护膝,但由于参赛选手临时增加,不但要求A厂家在原计划基础上增加10%的总量,而且还要比原计划提前3天完成.经预测,要完成新计划,平均每天的生产总量要比原计划多20对.求原计划每天生产多少对护膝.24. 已知:如图,是等边三角形,点D在边上,且是等边三角形,边与交于点O.过点E作 , 分别与线段相交于点F、G、H,联结 .
(1)、乙比甲晚 小时出发;乙出发 小时后追上甲;(2)、求乙比甲早几小时到达B地?23. 松江区于4月22日,举办“”上海佘山半程马拉松比赛.主办方打算为参赛选手定制一批护膝,并交由A厂家完成.已知A厂家要在规定的天数内生产3600对护膝,但由于参赛选手临时增加,不但要求A厂家在原计划基础上增加10%的总量,而且还要比原计划提前3天完成.经预测,要完成新计划,平均每天的生产总量要比原计划多20对.求原计划每天生产多少对护膝.24. 已知:如图,是等边三角形,点D在边上,且是等边三角形,边与交于点O.过点E作 , 分别与线段相交于点F、G、H,联结 .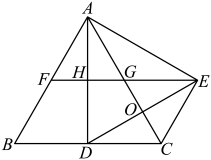 (1)、求证:四边形是平行四边形;(2)、连接 , 如果 , 求证:四边形是菱形.
(1)、求证:四边形是平行四边形;(2)、连接 , 如果 , 求证:四边形是菱形.