四川省成都市武侯区2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 以下是回收、绿色食品、绿色包装、低碳四个标志图案，其中为中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列因式分解正确的是（　　）

A、 $a (a - b) - b (b - a) = (a - b) (a + b)$ B、 $a^{2} - 4 b^{2} = (a + 4 b) (a - 4 b)$ C、 $a^{2} + 2 a b + {(- b)}^{2} = {(a - b)}^{2}$ D、 $a^{2} - a - 2 = a (a - 1) - 2$

查看试题解析
3. 一个不等式的解集在数轴上表示如图所示，则这个不等式可以是（　　）

A、 $1 - x > - 2$ B、 $x - 3 > 0$ C、 $2 x \leq 6$ D、 $3 - x \leq 0$

查看试题解析
4. 下列运算正确的是（）

A、 $\frac{a}{m} + \frac{b}{m} = \frac{a + b}{2 m}$ B、 $\frac{a}{x - y} - \frac{a}{y - x} = 0$ C、 $1 + \frac{1}{a} = \frac{2}{a}$ D、 $\frac{x}{x + y} + \frac{y}{y + x} = 1$

查看试题解析
5. 如图，小明荡秋千，位置从A点运动到了 $A^{'}$ 点，若 $∠ O A A^{'} = 50 °$ ，则秋千旋转的角度为（　　）

A、 $50 °$ B、 $60 °$ C、 $80 °$ D、 $90 °$

查看试题解析
6. 下列各命题中是真命题的是（　　）

A、两个锐角分别相等的两个直角三角形全等 B、两条直角边分别相等的两个直角三角形全等 C、平行四边形相邻的两个角都相等 D、一组对边平行，另一组对边相等的四边形是平行四边形

查看试题解析
7. 如图，将等边三角形 $A B C$ 纸片折叠，使得点A的对应点D落在 $B C$ 边上，其中折痕分别交边 $A B ， A C$ 于点E，F，连接 $D E ， D F$ ．若 $D F ⊥ B C$ ，则 $∠ A E F$ 的度数是（　　）

A、 $15 °$ B、 $30 °$ C、 $45 °$ D、 $60 °$

查看试题解析
8. 已知分式 $\frac{x + a}{2 x - b}$ (其中 $a$ ， $b$ 为常数 $)$ 满足表格中的信息：
          $x$ 的取值
          $0.5$
          $- 2$
          $m$
分式
无意义
值为 $0$
值为 $1$
则 $m$ 的值是(　　)

A、 $- 1$ B、 $1$ C、 $2$ D、 $3$

查看试题解析

二、填空题

9. 因式分解： $5 x^{2} - 5 =$ ．

查看试题解析
10. 定义：一个三角形的一边长是另一边长的2倍，这样的三角形叫做倍长三角形．若等腰 $△ A B C$ 是倍长三角形，腰 $A B$ 的长为10，则底边 $B C$ 的长为．

查看试题解析
11. 如图，一次函数 $y = k x + b$ 的图象与y轴正半轴相交于点A，与x轴正半轴相交于点B，且满足 $O A = 2$ ，则关于x的不等式 $k x + b > 2$ 的解集是．

查看试题解析
12. 如图，五边形 $A B C D E$ 是正五边形，若 $l_{1} / / l_{2}$ ，则 $∠ 1 - ∠ 2 =$ ．

查看试题解析
13. 如图，在 $△ A B C$ 中，按以下步骤作图：①分别以点B和C为圆心，以大于 $\frac{1}{2} B C$ 的长为半径作弧，两弧相交于点M和N；②作直线 $M N$ 交边 $A B$ 于点E．若 $A C = 10$ ， $B E = 8$ ， $∠ B = 45 °$ ，则 $A B$ 的长为．

查看试题解析

三、解答题

14.

(1)、解不等式组 ${\begin{array}{l} 2 x - 1 < 5 ① \\ \frac{4 - x}{2} \geq 1 ② \end{array}$

(2)、先化简，再求值： $\frac{1}{a - 1} \div (\frac{a^{2} + a}{a^{2} - 1} + \frac{1}{a - 1})$ ，其中 $a = - {(2023)}^{0} + {(\frac{1}{2})}^{- 1}$ ．

查看试题解析
15. 已知：如图，在 $▱ A B C D$ 中，点E，F分别为 $A D$ 和 $B C$ 的中点．求证：四边形 $B E D F$ 是平行四边形．

查看试题解析
16. 如图，方格纸中每个小正方形的边长都是1，建立平面直角坐标系 $x O y$ ，已知点A的坐标为 $(- 1 ， 3)$ ．

(1)、将点A先向右平移4个单位长度，再向下平移3个单位长度后得到点B，请画出 $△ O A B$ ，并直接写出点B的坐标；

(2)、在（1）的条件下，在y轴上取一点P，连接PB，若 $S_{Δ O P B} = \frac{4}{3} S_{Δ O A B}$ ，点P的坐标．

查看试题解析
17. 如图，D为 $△ A B C$ 内一点，连接 $D C$ 并延长至点E，使得 $C E = C D$ ．延长 $B C$ 至点F，使得 $C F = C B$ ，连接 $B D ， E F ， A E$ ．

(1)、求证： $E F ∥ B D$ ；

(2)、若 $∠ A C B = 90 °$ ， $B D ⊥ A E$ ，试探究线段 $A B ， A E ， B D$ 之间满足的数量关系．

查看试题解析
18. 如图1，在平面直角坐标系 $x O y$ 中，一次函数 $y = k x - 6 k + 6$ 的图象与一次函数 $y = - x + 6$ 的图象在第一象限相交于点 $A$ ，与 $y$ 轴正半轴相交于点 $B$ ．

(1)、若点 $A$ 的坐标为 $(2 ， n)$ ，分别求 $n$ ， $k$ 的值；

(2)、在(1)的条件下，是否存在点 $C$ ，使得以 $O$ ， $A$ ， $B$ ， $C$ 为顶点的四边形是平行四边形？若存在，求出点 $C$ 的坐标；若不存在，请说明理由；

(3)、如图2，连接 $O A$ ，过点 $O$ 作 $O D ⊥ O A$ 交直线 $A B$ 于点 $D$ ，试探究 $△ O B D$ 的形状．

查看试题解析

四、填空题

19. 已知 $x - 2 = 3 y$ ，则代数式 $x^{2} - 6 x y + 9 y^{2}$ 的值为．

查看试题解析
20. 生活中，我们所见到的地面常常是由一种或几种形状相同的图形拼接而成的．如图所示是由一块正三角形瓷砖与三块相同的正n边形瓷砖拼成的无缝隙、不重叠的地面的一部分，则n的值为．

查看试题解析
21. 若关于 $x$ 的分式方程 $\frac{1 - x}{x - 2} = \frac{m}{2 - x} - 2$ 的解小于 $3$ ，则 $m$ 的取值范围是

查看试题解析
22. 如图，在 $R t △ A B C$ 中， $∠ B = 90 ° ， ∠ A = 30 ° ， A B = 15$ ，点 $D ， E ， F$ 分别在边 $A B ， B C ， A C$ 上，连接 $D E ， E F ， D F$ ，若 $B D = 6$ ，且 $△ D E F$ 是等边三角形，则 $C F =$ ．

查看试题解析
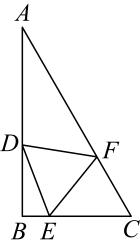23. 定义：在平面直角坐标系 $x O y$ 中，若点M关于直线 $x = m$ 的对称点 $M^{'}$ 在 $▱ A B C D$ 的内部（不包含边界），则称点M是 $▱ A B C D$ 关于直线 $x = m$ 的“伴随点”．如图，已知 $A (- 2 ， 0) ， B (3 ， 0) ， C (4 ， 4)$ 三点，连接 $B C$ ，以 $A B ， B C$ 为边作 $▱ A B C D$ ．若在直线 $y = x + n$ 上存在点N，使得点N是 $▱ A B C D$ 关于直线 $x = 2$ 的“伴随点”，则n的取值范围是．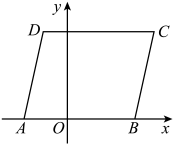

查看试题解析

五、解答题

24. 2023年3月10日，《成都市促进新能源汽车产业发展的实施意见》正式印发，该意见指出，结合未来新能源汽车充电需求，配建充电设施，鼓励对暂不具备建设条件的既有泊车位进行各类升级改造．某商场改造部分停车位为充电停车位，分别花费5万元和8万元购进了A，B两款充电桩，已知A款充电桩的单价比B款充电桩的单价高0.1万元，且购进B款充电桩的数量是A款充电桩的数量的2倍．

(1)、分别求A，B两款充电桩的单价；

(2)、该商场调研发现，现有改造的充电停车位已不能满足新能源汽车的充电需求，决定再用不多于 $9.58$ 万元的资金购进A，B两款充电桩共20个，求此次可购进A款充电桩的数量的最大值．

查看试题解析
25. 如图1，在 $▱ A B C D$ 中， $B C = n A B$ ，连接 $B D$ ， $∠ C B D = 30 °$ ，点E，F分别在边 $B C ， A D$ 上， $A E ， C F$ 分别交 $B D$ 于点G，H．将 $△ A B E$ ， $△ C D F$ 分别沿直线 $A E ， C F$ 折叠，使得点B的对应点 $B^{'}$ ，点D的对应点 $D^{'}$ 都落在对角线 $B D$ 上．

(1)、【尝试初探】求证： $△ A B G ≌ △ C D H$ ；

(2)、【深入探究】如图2，若点 $B^{'}$ ， $D^{'}$ 恰好分别与点H，G重合，求n的值；

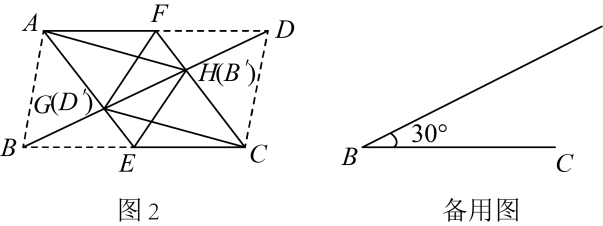(3)、【拓展延伸】若 $n = \sqrt{2}$ ，求 $\frac{B^{'} D^{'}}{B C}$ 的值．

查看试题解析
26. 【阅读理解】
在平面直角坐标系 $x O y$ 中，已知点R，S为平面内不重合的两点．给出如下定义：将点R绕点S顺时针旋转90度得到点 $R^{'}$ ，点 $R^{'}$ 关于y轴的对称点为 $R^{″}$ ，则称点 $R^{″}$ 为点R关于点S的“旋对点”．
【迁移应用】
如图，在平面直角坐标系 $x O y$ 中，直线 $y = x + 4$ 与x轴相交于点A，与y轴相交于点B．平面内有一点 $M (- 5 ， 1)$ ．

(1)、请在图中画出点M关于点O的“旋对点” $M^{″}$ ，并直接写出点M的坐标；

(2)、点Q为直线 $y = x + 4$ 上一动点．
①若点Q关于点M的“旋对点”为点 $Q^{″}$ ，试探究直线 $Q Q^{″}$ 经过某一定点，并求出该定点的坐标；
②在①的条件下，设直线 $Q Q^{″}$ 所经过的定点为H，取 $Q M$ 的中点N，连接 $N H$ ，求 $2 N H + Q H$ 的最小值．

查看试题解析

$x$ 的取值	$0.5$	$- 2$	$m$
分式	无意义	值为 $0$	值为 $1$