四川省成都市青羊区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 若分式的值为0,则x的值为( )A、2 B、-2 C、2或-2 D、02. 若ab,则下列不等式不一定成立的是( )A、a+3b+3 B、-2a-2b C、 D、a2b23. 下列多项式不能进行因式分解的是( )A、 B、 C、 D、4. 下列正多边形,绕其中心旋转后,能和自身重合的是 ( )A、
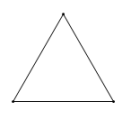 B、
B、 C、
C、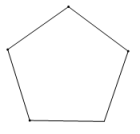 D、
D、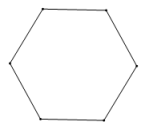 5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,沿着直线向右平移得到 , 与相交于点G,则以下四个结论:①;②;③;④ , 其中正确的是( )
5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,沿着直线向右平移得到 , 与相交于点G,则以下四个结论:①;②;③;④ , 其中正确的是( ) A、①②③ B、①②④ C、②④ D、①③④7. 如图,在中,是边的垂直平分线,分别交于D、E两点,连接 , , , 则的度数为( )
A、①②③ B、①②④ C、②④ D、①③④7. 如图,在中,是边的垂直平分线,分别交于D、E两点,连接 , , , 则的度数为( ) A、 B、 C、 D、8. 如图,四边形的对角线和相交于点O,下列条件不能判定四边形为平行四边形的是( )
A、 B、 C、 D、8. 如图,四边形的对角线和相交于点O,下列条件不能判定四边形为平行四边形的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 因式分解 = .10. 已知一个多边形的每个外角都是24°,此多边形是边形.11. 关于x的不等式的解集在数轴上表示如图,则k的值为 .
 12. 如图,在中,点D、E分别是的中点,以A为圆心,为半径作圆弧交于点F,若 , , 则的值为 .
12. 如图,在中,点D、E分别是的中点,以A为圆心,为半径作圆弧交于点F,若 , , 则的值为 . 13. 如图,的对角线AC,BD相交于点O,AC⊥BC,AC=2,BD=4,则AB= .
13. 如图,的对角线AC,BD相交于点O,AC⊥BC,AC=2,BD=4,则AB= .
三、解答题
-
14.(1)、解不等式组:;(2)、解分式方程:;(3)、先化简,再求值: , 其中 .15. 如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系的原点O在格点上,x轴、y轴都在网格线上,点A、B在格点上.
 (1)、将线段绕点O顺时针旋转得到线段 , 在图中画出线段 .(2)、线段与线段关于原点O成中心对称,在图中画出线段 .(3)、连接和 , 请直接写出四边形的面积为 .16. 成都环城生态公园项目是天府绿道体系“三环”中的重要一环,按照总体规划,环城生态公园项目将建成“5421”体系,让环城生态公园成为“绿色田园、天然公园、市民乐园”.在成都某个生态公园建设工程中,甲队单独施工50天可以完成该项工程,若甲队施工23天之后乙队加入,两队还需再同时施工12天,才能完成该项工程.若乙队单独施工完成此项工程需要多少天?17. 如图,在平面直角坐标系中,一次函数的图象与x轴交于点 , 与y轴交于点B,且与正比例函数的图象交于点 .
(1)、将线段绕点O顺时针旋转得到线段 , 在图中画出线段 .(2)、线段与线段关于原点O成中心对称,在图中画出线段 .(3)、连接和 , 请直接写出四边形的面积为 .16. 成都环城生态公园项目是天府绿道体系“三环”中的重要一环,按照总体规划,环城生态公园项目将建成“5421”体系,让环城生态公园成为“绿色田园、天然公园、市民乐园”.在成都某个生态公园建设工程中,甲队单独施工50天可以完成该项工程,若甲队施工23天之后乙队加入,两队还需再同时施工12天,才能完成该项工程.若乙队单独施工完成此项工程需要多少天?17. 如图,在平面直角坐标系中,一次函数的图象与x轴交于点 , 与y轴交于点B,且与正比例函数的图象交于点 . (1)、求m的值及一次函数解析式;(2)、点D在y轴上,当是以为直角边的直角三角形时,求点D的坐标.18. 如图,在四边形中, , .
(1)、求m的值及一次函数解析式;(2)、点D在y轴上,当是以为直角边的直角三角形时,求点D的坐标.18. 如图,在四边形中, , . (1)、求证:四边形为平行四边形;(2)、点E为边的中点,连接 , 过E作交边于点F,连接 .
(1)、求证:四边形为平行四边形;(2)、点E为边的中点,连接 , 过E作交边于点F,连接 .①求证:;
②若 , , , 求与的值.
四、填空题
-
19. 已知 , 则代数式的值是 .20. 关于x的方程的解是正数,则符合条件的a的所有正整数解之和为 .21. 如图,在平面直角坐标系中,直线交x轴于点A,交y轴于点B,在第一象限内有一点 , 当时,m的值为 .
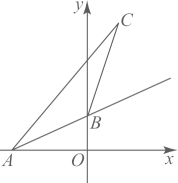 22. 如图,中 , , 平分交于点D,当为等腰三角形时,线段的值为 .
22. 如图,中 , , 平分交于点D,当为等腰三角形时,线段的值为 .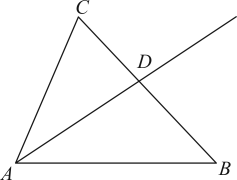 23. 如图,▱ABCD中∠D=75°,AB=4,AC=BC,点E为线段AD上一动点,过点E作EF⊥AC于点F,连接BE,点G为BE中点,连接GF.当GF最小时,线段AF的值为 .
23. 如图,▱ABCD中∠D=75°,AB=4,AC=BC,点E为线段AD上一动点,过点E作EF⊥AC于点F,连接BE,点G为BE中点,连接GF.当GF最小时,线段AF的值为 .
五、解答题
-
24. 近年来,成都市聚焦实现碳达峰碳中和目标,着力推进空间、产业、交通、能源结构优化调整,坚定不移走生态优先、绿色低碳的高质量发展道路.成都某新能源光伏企业计划生产A、B两种产品共10件,其生产成本和利润如下表.若工厂计划投入资金成本不超过38万元,且总利润不少于16万元.设生产A产品x件,总利润为y万元.(x取正整数)
A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)、求出y与x的关系式,并求出自变量x的取值范围;(2)、请求出总利润的最大值.25. 如图,中, , , 点是边上一动点,将绕点逆时针旋转得到 , 交边于点 , 连接 , 过点作平分交边于点 , 连接 . (1)、求证:;(2)、判断与的数量关系并证明;(3)、当时,若 , 求的面积.26. 如图,在平面直角坐标系中,点 , 点 , 点 , 以、为边作 , 点E为中点,连接、 .
(1)、求证:;(2)、判断与的数量关系并证明;(3)、当时,若 , 求的面积.26. 如图,在平面直角坐标系中,点 , 点 , 点 , 以、为边作 , 点E为中点,连接、 . (1)、分别求出线段和线段所在直线解析式;(2)、点P为线段上的一个动点,作点B关于点P的中心对称点F,设点P横坐标为a,用含a的代数式表示点F的坐标(不用写出a的取值范围);(3)、在(2)的条件下,
(1)、分别求出线段和线段所在直线解析式;(2)、点P为线段上的一个动点,作点B关于点P的中心对称点F,设点P横坐标为a,用含a的代数式表示点F的坐标(不用写出a的取值范围);(3)、在(2)的条件下,①当点F移动到的边上时,求点P坐标;
②M为中点,N为中点,连接、 . 请利用备用图探究,直接写出在点P的运动过程中,周长的最小值和此时点P的坐标.