四川省成都市金牛区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 下面图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若一个多边形的每个外角都是60°,则该多边形的边数为( ).A、9 B、8 C、7 D、63. 已知 , 则下列不等式一定成立的是( )A、 B、 C、 D、4. 若分式的值为0,则的值为( )A、 B、7 C、7或 D、495. 四边形的对角线交于点O,下列哪组条件不能判断四边形是平行四边形( )A、 , B、 , C、 , D、 ,6. 如图,在等腰中, , , , 的度数为( )
2. 若一个多边形的每个外角都是60°,则该多边形的边数为( ).A、9 B、8 C、7 D、63. 已知 , 则下列不等式一定成立的是( )A、 B、 C、 D、4. 若分式的值为0,则的值为( )A、 B、7 C、7或 D、495. 四边形的对角线交于点O,下列哪组条件不能判断四边形是平行四边形( )A、 , B、 , C、 , D、 ,6. 如图,在等腰中, , , , 的度数为( ) A、 B、 C、 D、7. 如图,在中,以点B为圆心,适当的长度为半径画弧分别交边于点P、Q,再分别以点P、Q为圆心,以大于为半径画弧,两弧交于点M,连接交于点E,过点E作交AB于点D,若 , , 则的周长为( )
A、 B、 C、 D、7. 如图,在中,以点B为圆心,适当的长度为半径画弧分别交边于点P、Q,再分别以点P、Q为圆心,以大于为半径画弧,两弧交于点M,连接交于点E,过点E作交AB于点D,若 , , 则的周长为( ) A、8 B、11 C、10 D、138. 《九章算术》中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到800里远的城市,所需时间比规定时间多1天;若改为快马派送,则所需时间比规定时间少2天,已知快马的速度是慢马的倍,求规定时间.设规定时间为天,则下列列出的分式方程正确的是( )A、 B、 C、 D、
A、8 B、11 C、10 D、138. 《九章算术》中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到800里远的城市,所需时间比规定时间多1天;若改为快马派送,则所需时间比规定时间少2天,已知快马的速度是慢马的倍,求规定时间.设规定时间为天,则下列列出的分式方程正确的是( )A、 B、 C、 D、二、填空题
-
9. 因式分解:= .10. 点向右平移4个单位,再向上平移1个单位后的坐标是 .11. 若关于的不等式的解集是 , 则的值为 .12. 如图,在边长为1的等边中,分别取三边的中点 , , , 得到 , 用同样的方法,得到 , 则的周长为 .
 13. 如图,有一架秋千,当它静止时,踏板离地米;将它往前推米时,踏板离地米,此时秋千的绳索是拉直的, , 则秋千的长度是米.
13. 如图,有一架秋千,当它静止时,踏板离地米;将它往前推米时,踏板离地米,此时秋千的绳索是拉直的, , 则秋千的长度是米.
三、解答题
-
14. 计算下列各题.(1)、解不等式组:;(2)、解方程:;(3)、先化简,再求值: , 其中 .15. 如图,在平面直角坐标系中,已知点 , , , 请解答下列问题:
 (1)、若先向右平移3个单位,然后向下平移2个单位得到 , 作出并写出三个顶点的坐标;(2)、将绕点O按逆时针方向旋转90°得到 , 作出 . (提示:作图时,先用2B铅笔作图,确定不再修改后用中性笔描黑)16. 随着退林复耕的全面推进,成都天府绕城生态公园也在向十万亩良田公园变身,其中有两块面积相等的良田公园作为小麦试验田,第一块使用原品种,第二块使用新品种,已知原品种种子比新品种每千克的单价少2元,且用700元购买的原品种种子千克数与用840元购买的新品种种子千克数相等,求原品种、新品种种子每千克的价格各是多少元?17. 如图,在四边形中, , 点E在上, .
(1)、若先向右平移3个单位,然后向下平移2个单位得到 , 作出并写出三个顶点的坐标;(2)、将绕点O按逆时针方向旋转90°得到 , 作出 . (提示:作图时,先用2B铅笔作图,确定不再修改后用中性笔描黑)16. 随着退林复耕的全面推进,成都天府绕城生态公园也在向十万亩良田公园变身,其中有两块面积相等的良田公园作为小麦试验田,第一块使用原品种,第二块使用新品种,已知原品种种子比新品种每千克的单价少2元,且用700元购买的原品种种子千克数与用840元购买的新品种种子千克数相等,求原品种、新品种种子每千克的价格各是多少元?17. 如图,在四边形中, , 点E在上, . (1)、求证:四边形是平行四边形;(2)、若 , 平分 , , 求的长.18. 在中, , , , 点D是线段上的动点,交AC于点E,分别交射线、射线于点F、G,连结 .
(1)、求证:四边形是平行四边形;(2)、若 , 平分 , , 求的长.18. 在中, , , , 点D是线段上的动点,交AC于点E,分别交射线、射线于点F、G,连结 . (1)、如图1,若点G恰好平分 , 判断四边形的形状并证明;(2)、如图2,设的长为x,的面积为y,求出y关于x的函数关系式;(3)、当时,求的长.
(1)、如图1,若点G恰好平分 , 判断四边形的形状并证明;(2)、如图2,设的长为x,的面积为y,求出y关于x的函数关系式;(3)、当时,求的长.四、填空题
-
19. 已知 , , 则 .20. 关于x的分式方程有增根,则 .21. 如图,一次函数与的图象相交于点 , 则关于的不等式组的解集为 .
 22. 在中, , , , , 将沿剪开成两个三角形,把这两个三角形拼成一个平行四边形.在拼成的平行四边形中,对角线长度的最大值是 .
22. 在中, , , , , 将沿剪开成两个三角形,把这两个三角形拼成一个平行四边形.在拼成的平行四边形中,对角线长度的最大值是 . 23. 在平面直角坐标系中,已知点 , , , , 给出如下定义:若点P关于直线:的对称点Q在四边形的内部或边上,则称该点P为四边形关于直线的“相关点”,点是四边形关于直线:的“相关点”,且是以为腰的等腰三角形,则m的值为;直线上存在点P,使得点P是四边形关于直线:的“相关点”,则的取值范围为 .
23. 在平面直角坐标系中,已知点 , , , , 给出如下定义:若点P关于直线:的对称点Q在四边形的内部或边上,则称该点P为四边形关于直线的“相关点”,点是四边形关于直线:的“相关点”,且是以为腰的等腰三角形,则m的值为;直线上存在点P,使得点P是四边形关于直线:的“相关点”,则的取值范围为 .五、解答题
-
24. 第31届世界大学生夏季运动会将于2023年7月28日至2023年8月8日在成都举行,这一届的吉祥物“蓉宝”是以大熊猫“芝麻”为原型设计,某公司生产的吉祥物摆件有445箱,蓉宝挂件有130箱.(1)、现计划租用A,B两种货车共15辆,一次性将物品送往仓库,已知A种货车可装摆件35箱和挂件10箱,B种货车可装摆件15箱和挂件15箱,则一共有几种租车方案?(2)、在(1)的条件下,A种货车每辆需运费860元,B种货车每辆需运费740元,怎样租车才能使总运费最少?并求出最少运费.25. 在平面直角坐标系中,直线分别交x轴、y轴于点C、B,直线与x轴负半轴交于点A,与y轴交于点B.
 (1)、如图1,求的面积;(2)、如图2,作于点E,延长交直线于点D,请在平面内找一点P,使得以P、D、B、E为顶点的四边形是平行四边形,直接写出这样的点P的坐标;(3)、如图3,在(2)的条件下,点F在线段上,点G在线段上,若 , , 求点F的坐标.26. 在中, , 点为直线BC上一动点, , .
(1)、如图1,求的面积;(2)、如图2,作于点E,延长交直线于点D,请在平面内找一点P,使得以P、D、B、E为顶点的四边形是平行四边形,直接写出这样的点P的坐标;(3)、如图3,在(2)的条件下,点F在线段上,点G在线段上,若 , , 求点F的坐标.26. 在中, , 点为直线BC上一动点, , .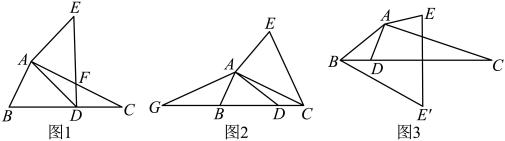 (1)、如图1,连接交于 , , 为中点,若 , , 求的长;(2)、如图2,延长至点使得 , 连接 , 求证:;(3)、如图3, , , 作点关于直线的对称点 , 连接 , , 当最小时,直接写出线段的长.
(1)、如图1,连接交于 , , 为中点,若 , , 求的长;(2)、如图2,延长至点使得 , 连接 , 求证:;(3)、如图3, , , 作点关于直线的对称点 , 连接 , , 当最小时,直接写出线段的长.