四川省达州市达川区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 下列奥运会会徽图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列由左到右的变形,属于因式分解的( )A、 B、 C、 D、3. 若分式 的值为0,则x的值为( )A、-2 B、0 C、2 D、±24. 如图,是不等式组的解集在数轴上的正确表示,则的值是( )
2. 下列由左到右的变形,属于因式分解的( )A、 B、 C、 D、3. 若分式 的值为0,则x的值为( )A、-2 B、0 C、2 D、±24. 如图,是不等式组的解集在数轴上的正确表示,则的值是( )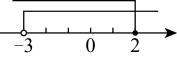 A、 B、 C、6 D、95. 下列说法错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则6. 下列命题中是真命题的是( )A、一组对边平行,一组对角相等的四边形是平行四边形 B、一组边、一组角对应相等的两个直角三角形全等 C、若等腰三角形的一个外角等于 , 则该等腰三角形的顶角等于 D、三角形中,三边的垂直平分线的交点到三边的距离相等7. 如图,在平行四边形中,对角线相交于点O,E是的中点,连接 . 若 , 的周长为9,则平行四边形的周长为( )
A、 B、 C、6 D、95. 下列说法错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则6. 下列命题中是真命题的是( )A、一组对边平行,一组对角相等的四边形是平行四边形 B、一组边、一组角对应相等的两个直角三角形全等 C、若等腰三角形的一个外角等于 , 则该等腰三角形的顶角等于 D、三角形中,三边的垂直平分线的交点到三边的距离相等7. 如图,在平行四边形中,对角线相交于点O,E是的中点,连接 . 若 , 的周长为9,则平行四边形的周长为( )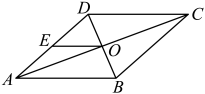 A、17 B、20 C、26 D、348. 如图,已知是的平分线, , 若 , 则的面积( )
A、17 B、20 C、26 D、348. 如图,已知是的平分线, , 若 , 则的面积( )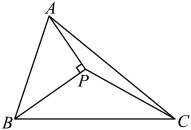 A、 B、 C、 D、不能确定9. 某中学为使初三学生在中考体育测试中取得优异的成绩,在4月初安排全校体育教师对初三全体学生进行了一次摸拟检测,在这一次检测中,甲组教师完成300个学生检测,乙组教师完成270个学生检测;已知甲组教师比乙组教师平均每分钟多检测4个学生,所用时间比乙组教师少用30分钟,求本次检测中甲、乙两组教师平均每分钟各检测多少个学生?设甲组教师平均每分钟检测x个学生,则由题意可列方程为( )A、 B、 C、 D、10. 如图,四边是平行四边形, , 与的延长线交于点E,连接交于F,连接 , 下列结论中:①四边形是平行四边形;②;③若 , 则;④若 , 则是直角三角形,正确的结论有( )
A、 B、 C、 D、不能确定9. 某中学为使初三学生在中考体育测试中取得优异的成绩,在4月初安排全校体育教师对初三全体学生进行了一次摸拟检测,在这一次检测中,甲组教师完成300个学生检测,乙组教师完成270个学生检测;已知甲组教师比乙组教师平均每分钟多检测4个学生,所用时间比乙组教师少用30分钟,求本次检测中甲、乙两组教师平均每分钟各检测多少个学生?设甲组教师平均每分钟检测x个学生,则由题意可列方程为( )A、 B、 C、 D、10. 如图,四边是平行四边形, , 与的延长线交于点E,连接交于F,连接 , 下列结论中:①四边形是平行四边形;②;③若 , 则;④若 , 则是直角三角形,正确的结论有( )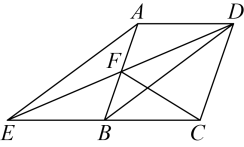 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
11. 若关于x的不等式组的解集是 , 则a的取值范围是 .12. 如图,在中, , 边的垂直平分线交于点D,交于点E.若 , 则的度数为 .
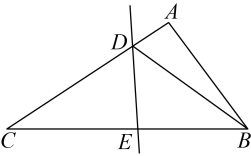 13. ∵ , ∴ , 这说明能被整除,即或是的一个因式.另外,当即时,多项式的值为0;当即时,多项式的值为0.若能被整除,则k的值是 .14. 已知关于x的分式方程的解为负数,则m的取值范围是 .15. 如图,在中, , , , 以点A为圆心,任意长度为半径画弧,分别交于点M、N,再分别以点M、N为圆心,大于的长为半径画弧,两弧交于点O,连接并延长交于点D,以为边作平行四边形 , 则平行四边形的面积是 .
13. ∵ , ∴ , 这说明能被整除,即或是的一个因式.另外,当即时,多项式的值为0;当即时,多项式的值为0.若能被整除,则k的值是 .14. 已知关于x的分式方程的解为负数,则m的取值范围是 .15. 如图,在中, , , , 以点A为圆心,任意长度为半径画弧,分别交于点M、N,再分别以点M、N为圆心,大于的长为半径画弧,两弧交于点O,连接并延长交于点D,以为边作平行四边形 , 则平行四边形的面积是 .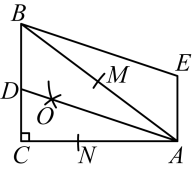
三、解答题
-
16.(1)、解分式方程:(2)、解不等式组 , 把解集在数轴表示出来.17. 先化简: , 再从、、0、1四个数中挑选一个自己喜欢的整数代入求值.18. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,的三个顶点 , , 均在格点上,
 (1)、画出将向下平移4个单位长度得到的;(2)、画出绕点C逆时针旋转后得到的 , 并写出点的坐标;(3)、求点A到点经过的路径长度.19. 如图,在中, , 的平分线交于点D,点E在上,且 , 过点B作交的延长线于点F.
(1)、画出将向下平移4个单位长度得到的;(2)、画出绕点C逆时针旋转后得到的 , 并写出点的坐标;(3)、求点A到点经过的路径长度.19. 如图,在中, , 的平分线交于点D,点E在上,且 , 过点B作交的延长线于点F.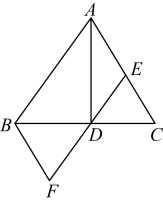 (1)、求证:四边形是平行四边形;(2)、若 , 求的长.20. 某精品水果店老板在“五·一”劳动节期间,第一次购进有机草莓20千克,有机西瓜40千克,共用去1580元,很快售完;老板第二次又购进有机草莓45千克,有机西瓜60千克,共用去3195元,两次的进价相同.(1)、求有机草莓、西瓜每千克进价各是多少元?(2)、水果店以每千克70元的价格销售第二次购进的有机草莓,售出60%后,因有机草莓存放时间短,必须尽快售完,故决定打折促销,要使第二次草莓的销售总利润不少于423元,剩余的草莓每千克售价最低打几折?21. 如图,四边形是平行四边形,的平分线交对角线于点E,交于点H,交的延长线于点F,且 , .
(1)、求证:四边形是平行四边形;(2)、若 , 求的长.20. 某精品水果店老板在“五·一”劳动节期间,第一次购进有机草莓20千克,有机西瓜40千克,共用去1580元,很快售完;老板第二次又购进有机草莓45千克,有机西瓜60千克,共用去3195元,两次的进价相同.(1)、求有机草莓、西瓜每千克进价各是多少元?(2)、水果店以每千克70元的价格销售第二次购进的有机草莓,售出60%后,因有机草莓存放时间短,必须尽快售完,故决定打折促销,要使第二次草莓的销售总利润不少于423元,剩余的草莓每千克售价最低打几折?21. 如图,四边形是平行四边形,的平分线交对角线于点E,交于点H,交的延长线于点F,且 , .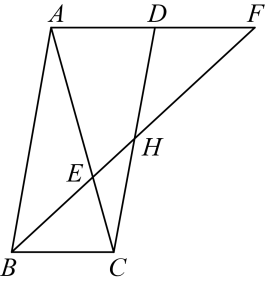 (1)、求的度数;(2)、判断:是否是等腰三角形?并说明理由.22. 如图,平行四边形的对角线与相交于点O,点E为的中点,过点A作交的延长线于点F,连接 .
(1)、求的度数;(2)、判断:是否是等腰三角形?并说明理由.22. 如图,平行四边形的对角线与相交于点O,点E为的中点,过点A作交的延长线于点F,连接 .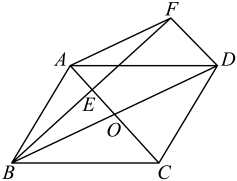 (1)、求证:四边形是平行四边形.(2)、若 , , , 求平行四边形的面积.23. 我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、添项拆项法、十字相乘法等等.①分组分解法:将一个多项式适当分组后,可提公因式或运用公式继续分解的方法叫作分组分解法.
(1)、求证:四边形是平行四边形.(2)、若 , , , 求平行四边形的面积.23. 我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、添项拆项法、十字相乘法等等.①分组分解法:将一个多项式适当分组后,可提公因式或运用公式继续分解的方法叫作分组分解法.例如:
②十字相乘法:十字相乘法能用于二次三项式的分解因式.
分解步骤:1.分解二次项,所得结果分别写在十字交叉线的左上角和左下角;2.分解常数项,所得结果分别写在十字交叉线的右上角和右下角;3.交叉相乘,求代数和,使其等于一次项;4.观察得出原二次三项式的两个因式,并表示出分解结果.这种分解方法叫作十字相乘法.
例如: 分析:
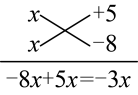
观察得出:两个因式分别为与
解:原式
③添项拆项法:将一个多项式的某一项拆成两项后,可提公因式或运用公式继续分解的方法叫作拆项法.
例如: .
(1)、仿照以上方法,按照要求分解因式:①(分组分解法);
②(十字相乘法);
(2)、已知:a、b、c为的三条边, , 判断的形状.24. 由于受到手机更新换代的影响,某手机店经销的华为Mate30手机二月份每台售价比一月份每台售价低500元.如果卖出相同数量的华为Mate30手机,那么一月份销售额为9万元,二月份销售额只有8万元.(1)、一月份Mate30手机每台售价为多少元?(2)、为了提高利润,该店计划三月份购进华为Mate40手机销售,已知华为Mate30每台进价为3500元,华为Mate40每台进价为4000元,预计用不少于7.4万元且不多于7.6万元的资金购进这两种手机共20台,请问有几种进货方案?(3)、该店计划4月份对华为Mate30的尾货进行销售,决定在二月份售价基础上每售出一台华为Mate30手机再返还顾客现金 元,而华为Mate40按销售价4400元销售,如要使(2)中所有方案获利相同, 应取何值?25. 如图所示,在平行四边形中, , 点F是的中点,连接 , 延长交的延长线于点H,平分交于点E.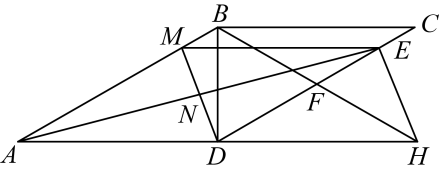 (1)、若 , , 求的长;(2)、点M在上,满足 , 连接交于点N,求证四边形是平行四边形;(3)、在(2)的条件下,若 , 求证: .
(1)、若 , , 求的长;(2)、点M在上,满足 , 连接交于点N,求证四边形是平行四边形;(3)、在(2)的条件下,若 , 求证: .