四川省达州市通川区2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 世界上最小的鸟是生活在古巴的吸蜜蜂鸟，它的质量约为0.056盎司.将0.056用科学记数法表示为（）

A、5.6×10^﹣¹ B、5.6×10^﹣² C、5.6×10^﹣³ D、0.56×10^﹣¹

查看试题解析
2. 在以下回收、绿色食品、节能、节水四个标志中，是中心对称图形的是（）.

A、 B、 C、 D、

查看试题解析
3. 化简分式 $\frac{7 a + 7 b}{a^{2} - b^{2}}$ 的结果是（）

A、 $\frac{a + b}{7}$ B、 $\frac{7}{a + b}$ C、 $\frac{7}{a - b}$ D、 $\frac{a - b}{7}$

查看试题解析
4. 下面式子从左边到右边的变形是因式分解的是（）

A、 $x^{2} - 4 x + 4 = {(x - 2)}^{2}$ B、 $x^{2} - x - 2 = x (x - 1) - 2$ C、 $(x + 1) (x - 1) = x^{2} - 1$ D、 $x - \frac{1}{x} = x (1 - \frac{1}{x})$

查看试题解析
5. 如图所示，在 $▱ A B C D$ 中，对角线 $A C$ ， $B D$ 交于点O， $O E ∥ B C$ 交 $C D$ 于E．若 $O E = 3 c m$ ，则 $A D$ 的长为（）

A、3 $c m$ B、6 $c m$ C、9 $c m$ D、12 $c m$

查看试题解析
6. 解关于 $x$ 的方程 $\frac{x - 6}{x - 5} + 1 = \frac{m}{x - 5}$ （其中m为常数）产生增根，则常数m的值等于（）

A、-2 B、2 C、-1 D、1

查看试题解析
7. 如图，已知在 $△ A B C$ 中， $∠ A B C < 90 °$ ， $A B \neq B C ， B E$ 是 $A C$ 边上的中线．按下列步骤作图：①分别以点 $B ， C$ 为圆心，大于线段 $B C$ 长度一半的长为半径作弧，相交于点 $M ， N$ ；②过点 $M ， N$ 作直线 $M N$ ，分别交 $B C$ ， $B E$ 于点 $D ， O$ ；③连结 $C O ， D E$ ．则下列结论错误的是（）

A、 $O B = O C$ B、 $∠ B O D = ∠ C O D$ C、 $D E / / A B$ D、 $D B = D E$

查看试题解析
8. 定义一种新运算：当 $a > b$ 时， $a * b = a b + b$ ；当 $a < b$ 时， $a * b = a b - b$ ．若 $3 * (x + 2) > 0$ ，则x的取值范围是（）

A、 $- 1 < x < 1$ 或 $x < - 2$ B、 $x < - 2$ 或 $1 < x < 2$ C、 $- 2 < x < 1$ 或 $x > 1$ D、 $x < - 2$ 或 $x > 2$

查看试题解析
9. 如图，把长方形纸片 $A B C D$ 沿对角线折叠，设重叠部分为 $△ E B D$ ，那么，有下列说法：
① $△ B D E$ 是等腰三角形， $E B = E D$ ；②折叠后 $∠ A B E$ 和 $∠ D B F$ 一定相等；③折叠后得到的图形是轴对称图形；④ $△ A B E$ 和 $△ D E F$ 一定是全等三角形．其中正确的是（）

A、①②③ B、①③④ C、①②④ D、①②③④

查看试题解析
10. 如图在平面直角坐标系 $x O y$ 中，有一个等腰直角三角形 $A O B$ ， $∠ O A B = 90 °$ ，直角边 $A O$ 在x轴上，且 $A O = 1$ ．将 $R t △ A O B$ 绕原点O顺时针旋转 $90 °$ 得到等腰直角三角形 $A_{1} O B_{1}$ ，且 $A_{1} O = 2 A O$ ，再将 $R t △ A_{1} O B_{1}$ 绕原点O顺时针旋转90°得到等腰三角形 $A_{2} O B_{2}$ ，且 $A_{2} O = 2 A_{1} O$ ……，依此规律，得到等腰直角三角形 $A_{2023} O B_{2023}$ ．则点 $B_{2023}$ 的坐标（）

A、 $(- 2^{2023} ， 2^{2023})$ B、 $(2^{2022} ， - 2^{2022})$ C、 $(2^{2023} ， - 2^{2023})$ D、 $(2^{2022} ， 2^{2022})$

查看试题解析

二、填空题

11. 若分式 $\frac{2 - | x |}{x + 2}$ 的值为零，则x的值为.

查看试题解析
12. 点 $(- \frac{1}{2} ， m)$ 和点 $(2 ， n)$ 在直线 $y = 2 x + b$ 上，则m与n的大小关系是．

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ， $B D$ 平分 $∠ A B C$ ， $D E ⊥ A B$ 于E，若 $△ A D E$ 的周长为 $2 \sqrt{2}$ ，则 $△ A B C$ 的面积为．

查看试题解析
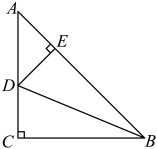14. 如图，将正方形网格放置在平面直角坐标系中，其中，每个小正方形的边长均为1，点A ， B ， C的坐标分别为 $A (0 ， 3)$ ， $B (- 1 ， 1)$ ， $C (3 ， 1)$ ． $△ A^{'} B^{'} C^{'}$ 是 $△ A B C$ 关于 $x$ 轴的对称图形，将 $△ A^{'} B^{'} C^{'}$ 绕点 $B^{'}$ 逆时针旋转180°，点 $A^{'}$ 的对应点为M ，则点M的坐标为．

查看试题解析
15. 已知：如图， $B D$ 为 $△ A B C$ 的角平分线，且 $B D = B C$ ， E为 $B D$ 延长线上的一点， $B E = B A$ ，过E作 $E F ⊥ A B$ ， F为垂足．下列结论：① $△ A B D ≌ △ E B C$ ；② $∠ B C E + ∠ B C D = 180 °$ ；③ $A D = A E = E C$ ；④ $A B + B C = 2 B F$ ．其中正确的是．（只填序号）

查看试题解析

三、解答题

16.

(1)、解不等式组： ${\begin{array}{l} x + 1 \geq 2 \\ 5 x \leq 4 x + 3 \end{array}$ ，并把不等式组的解集在数轴上表示出来

(2)、先化简，再求值： $\frac{x}{x - 2} \div \frac{x^{2} - 2 x}{x^{2} - 4} - \frac{2}{x - 2}$ ，其中 $x = \frac{3}{2}$

查看试题解析
17. 为贯彻落实党中央关于全面建成小康社会的战略部署，某贫困地区的广大党员干部深入农村积极开展“精准扶贫”工作．经过多年的精心帮扶，截至2019年底，按照农民人均年纯收入3218元的脱贫标准，该地区只剩少量家庭尚未脱贫．现从这些尚未脱贫的家庭中随机抽取50户，统计其2019年的家庭人均年纯收入，得到如下图所示的条形图．

(1)、如果该地区尚未脱贫的家庭共有1000户，试估计其中家庭人均年纯收入低于2000元（不含2000元）的户数；

(2)、估计2019年该地区尚未脱贫的家庭人均年纯收入的平均值；

(3)、2020年初，由于新冠疫情，农民收入受到严重影响，上半年当地农民家庭人均月纯收入的最低值变化情况如下面的折线图所示．为确保当地农民在2020年全面脱贫，当地政府积极筹集资金，引进某科研机构的扶贫专项项目．据预测，随着该项目的实施，当地农民自2020年6月开始，以后每月家庭人均月纯收入都将比上一个月增加170元．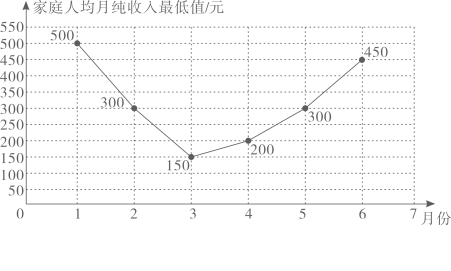

已知2020年农村脱贫标准为农民人均年纯收入4000元，试根据以上信息预测该地区所有贫困家庭能否在今年实现全面脱贫．

查看试题解析
18. 小刚去超市购买画笔，第一次花60元买了若干支A型画笔，第二次超市推荐了B型画笔，但B型画笔比A型画笔的单价贵2元，他又花100元买了相同支数的B型画笔．

(1)、超市B型画笔单价多少元？

(2)、小刚使用两种画笔后，决定以后使用B型画笔，但感觉其价格稍贵，和超市沟通后，超市给出以下优惠方案：一次购买不超过20支，则每支B型画笔打九折；若一次购买超过20支，则前20支打九折，超过的部分打八折．设小刚购买的B型画笔x支，购买费用为y元，请写出y关于x的函数关系式．

(3)、在（2）的优惠方案下，若小刚计划用270元购买B型画笔，则能购买多少支B型画笔？

查看试题解析
19. 如果一个分式的分子或分母可以因式分解，且这个分式不可约分，那么我们称这个分式为“和谐分式”．

(1)、下列分式：① $\frac{x - 1}{x^{2} + 1}$ ；② $\frac{a - 2 b}{a^{2} - b^{2}}$ ；③ $\frac{x + y}{x^{2} - y^{2}}$ ；④ $\frac{a^{2} - b^{2}}{{(a + b)}^{2}}$ ．其中是“和谐分式”是　　（填写序号即可）；

(2)、若a为正整数，且 $\frac{x - 1}{x^{2} + a x + 4}$ 为“和谐分式”，请写出a的值；

(3)、在化简 $\frac{4 a^{2}}{a b^{2} - b^{3}} - \frac{a}{b} \div \frac{b}{4}$ 时，
小东和小强分别进行了如下三步变形：

小东：原式= $\frac{4 a^{2}}{a b^{2} - b^{3}} - \frac{a}{b} \times \frac{4}{b}$ = $\frac{4 a^{2}}{a b^{2} - b^{3}} - \frac{4 a}{b^{2}}$ = $\frac{4 a^{2} b^{2} - 4 a (a b^{2} - b^{3})}{(a b^{2} - b^{3}) b^{2}}$ ，

小强：原式= $\frac{4 a^{2}}{a b^{2} - b^{3}} - \frac{a}{b} \times \frac{4}{b}$ = $\frac{4 a^{2}}{b^{2} (a - b)} - \frac{4 a}{b^{2}} = \frac{4 a^{2} - 4 a (a - b)}{(a - b) b^{2}}$ ，

显然，小强利用了其中的和谐分式，第三步所得结果比小东的结果简单，原因是：　　，

请你接着小强的方法完成化简．

查看试题解析
20. 在现今“互联网＋”的时代，密码与我们的生活已经密不可分．而诸如“123456”、生日等简单密码又容易被破解，因此利用简单方法产生一组容易记忆的密码就很有必要了．有一种用“因式分解”法产生的密码，方便记忆，其原理是：将一个多项式分解因式，如多项式： $x^{3} + 2 x^{2} - x - 2$ 因式分解的结果为 $(x - 1) (x + 1) (x + 2)$ ，当 $x = 18$ 时， $x - 1 = 17$ ， $x + 1 = 19$ ， $x + 2 = 20$ ，此时可以得到六位数的数字密码171920．

(1)、根据上述方法，当 $x = 21$ ， $y = 7$ 时，对于多项式 $x^{3} - x y^{2}$ 分解因式后可以形成哪些数字密码（写出三个）

(2)、若一个直角三角形的周长是30，斜边长为13，其中两条直角边分别为x、y，求出一个由多项式 $x^{3} y + x y^{3}$ 分解因式后得到的六位数的数字密码（只需一个即可）；

(3)、若多项式 $x^{3} + (m - 3 n) x^{2} - n x - 21$ 因式分解后，利用本题的方法，当 $x = 27$ 时可以得到其中一个六位数的数字密码为242834，求m、n的值．

查看试题解析
21.

(1)、如图，在正方形网格中， $△ A B C$ 的顶点在格点上．请仅用无刻度直尺完成以下作图（保留作图痕迹）．
①在图1中，作 $△ A B C$ 关于点O对称的 $△ A^{'} B^{'} C^{'}$ ；

②在图2中，作 $△ A B C$ 绕点A顺时针旋转一定角度后，顶点仍在格点上的 $△ A^{'} B^{'} C^{'}$ ．


(2)、如图，已知线段a，点A在平面直角坐标系 $x O y$ 内．用直尺和圆规在第一象限内作出点P，使点P（P到两坐标轴的距离相等，且与点A的距离等于a．（保留作图痕迹，不写作法，要求写出结论）


查看试题解析
22.

(1)、问题1：如图①，在四边形 $A B C D$ 中， $∠ B = ∠ C = 90 °$ ， $P$ 是 $B C$ 上一点， $P A = P D$ ， $∠ A P D = 90 °$ ．求证： $A B + C D = B C$ ．

(2)、问题2：如图②，在四边形 $A B C D$ 中， $∠ B = ∠ B C D = 45 °$ ， $P$ 是 $B C$ 上一点，过点 $P$ 作 $D P ⊥ A P$ 于P， $D P = A P$ ，连接 $A D$ ．过点C作 $C E ∥ A B$ 交 $A P$ 的延长线于点E连接 $D E$ ．求证： $D E = D A$ ．

查看试题解析
23. 阅读材料：
我们定义：如果一个数的平方等于-1，记作i²=-1，那么这个i就叫做虚数单位．虚数与我们学过的实数合在一起叫做复数．一个复数可以表示为a+bi（a，b均为实数）的形式，其中a叫做它的实部，b叫做它的虚部．
复数的加、减、乘的运算与我们学过的整式加、减、乘的运算类似．
例如计算：（5+i）+（3-4i）=（5+3）+（i-4i）=8-3i．
根据上述材料，解决下列问题：

(1)、填空：i³= ， i⁴=；

(2)、计算：（2+i）²；

(3)、将 $\frac{1 + i}{1 - i}$ 化为a+bi（a，b均为实数）的形式（即化为分母中不含i的形式）．

查看试题解析
24. 某商场为了促销，设计了抽奖活动，方案如下：根据不同的消费金额，每次抽奖时可以从100张面值分别为1元、2元、3元、…、100元的奖券中（面值为整数），一次任意抽取2张、3张、4张、…等若干张奖券，奖券的面值金额之和即为优惠金额．某顾客获得了一次抽取5张奖券的机会，小明想知道该顾客共有多少种不同的优惠金额？
问题建模：

从1，2，3，…，n（n为整数，且 $n \geq 3$ ）这n个整数中任取 $a (1 < a < n)$ 个整数，这a个整数之和共有多少种不同的结果？

模型探究：

我们采取一般问题特殊化的策略，先从最简单的情形入手，再逐次递进，从中找出解决问题的方法．

(1)、探究一：①从1，2，3这3个整数中任取2个整数，这2个整数之和共有多少种不同的结果？
表①

所取的2个整数
1，2
1，3
2，3
2个整数之和
3
4
5
如表①，所取的2个整数之和可以为3，4，5，也就是从3到5的连续整数，其中最小是3，最大是5，所以共有3种不同的结果．
②从1，2，3，4这4个整数中任取2个整数，这2个整数之和共有多少种不同的结果？
表②

所取的2个整数
1，2
1，3
1，4
2，3
2，4
3，4
2个整数之和
3
4
5
5
6
7
如表②，所取的2个整数之和可以为3，4，5，6，7，也就是从3到7的连续整数，其中最小是3，最大是7，所以共有5种不同的结果．
③从1，2，3，4，5这5个整数中任取2个整数，这2个整数之和共有种不同的结果．
④从1，2，3，…，n（n为整数，且 $n \geq 3$ ）这n个整数中任取2个整数，这2个整数之和共有种不同的结果．

(2)、探究二：
①从1，2，3，4这4个整数中任取3个整数，这3个整数之和共有种不同的结果．
②从1，2，3，…，n（n为整数，且 $n \geq 4$ ）这n个整数中任取3个整数，这3个整数之和共有种不同的结果．

(3)、探究三：从1，2，3，…，n（n为整数，且 $n \geq 5$ ）这n个整数中任取4个整数，这4个整数之和共有种不同的结果．

(4)、归纳结论：从1，2，3，…，n（n为整数，且 $n \geq 3$ ）这n个整数中任取 $a (1 < a < n)$ 个整数，这a个整数之和共有种不同的结果．

(5)、问题解决：从100张面值分别为l元、2元、3元、…、100元的奖券中（面值为整数），一次任意抽取5张奖券，共有种不同的优惠金额．

(6)、拓展延伸：
①从l，2，3，…，n（n为整数，且 $n \geq 6$ ）这n个整数中任取6个整数，使得取出的这些整数之和共有2023种不同的结果？（写出解答过程）

②从3，4，5，…， $n + 3$ （n为整数，且 $n \geq 2$ ）这 $(n + 1)$ 个整数中任取 $a (1 < a < n + 1)$ 个整数，这a个整数之和共有种不同的结果．

查看试题解析
25. 在一次数学研究性学习中，小兵将两个全等的直角三角形纸片ABC和DEF拼在一起，使点A与点F重合，点C与点D重合（如图1），其中∠ACB＝∠DFE＝90°，BC＝EF＝3cm，AC＝DF＝4cm，并进行如下研究活动．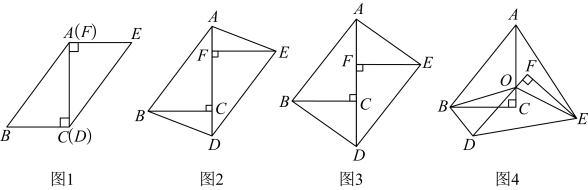

活动一：将图1中的纸片DEF沿AC方向平移，连结AE，BD（如图2），当点F与点C重合时停止平移．

(1)、【思考】图2中的四边形ABDE是平行四边形吗？请说明理由．

(2)、【发现】当纸片DEF平移到某一位置时，小兵发现四边形ABDE为矩形（如图3）．求AF的长．

(3)、活动二：在图3中，取AD的中点O，再将纸片DEF绕点O顺时针方向旋转α度（0≤α≤90），连结OB，OE（如图4）．
【探究】当EF平分∠AEO时，探究OF与BD的数量关系，并说明理由．

查看试题解析

所取的2个整数	1，2	1，3	1，4	2，3	2，4	3，4
2个整数之和	3	4	5	5	6	7