四川省达州市渠县2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 依据所标数据,下列图形中一定为平行四边形的是( )A、
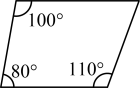 B、
B、 C、
C、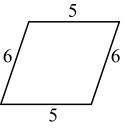 D、
D、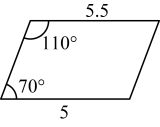 2. 在平面直角坐标系中,若点在第二象限,则的取值范围在数轴上表示正确的是( )A、
2. 在平面直角坐标系中,若点在第二象限,则的取值范围在数轴上表示正确的是( )A、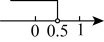 B、
B、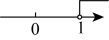 C、
C、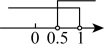 D、
D、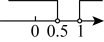 3. 下列说法,错误的是( )A、一个三角形两边的垂直平分线的交点到这个三角形三个顶点的距离相等 B、“若 , 则”的逆命题是假命题 C、在角的内部到角的两边距离相等的点一定在这个角的平分线上 D、用反证法证明“三角形中必有一个角不大于”,先假设这个三角形中有一个内角大于60°4. 如图,边长为的长方形周长为12,面积为5,则的值为( )
3. 下列说法,错误的是( )A、一个三角形两边的垂直平分线的交点到这个三角形三个顶点的距离相等 B、“若 , 则”的逆命题是假命题 C、在角的内部到角的两边距离相等的点一定在这个角的平分线上 D、用反证法证明“三角形中必有一个角不大于”,先假设这个三角形中有一个内角大于60°4. 如图,边长为的长方形周长为12,面积为5,则的值为( )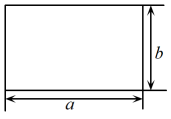 A、60 B、120 C、130 D、2405. 表格第一列是王江化简分式的部分计算过程,则在化简过程中的横线上依次填入的表格第二列内容的序号为( )
A、60 B、120 C、130 D、2405. 表格第一列是王江化简分式的部分计算过程,则在化简过程中的横线上依次填入的表格第二列内容的序号为( )原式
①
②
③
④
A、④①② B、③①② C、③②① D、④②①6. 若关于x的分式方程有增根,则m的值为( )A、1 B、2 C、3 D、47. 若某多边形的边数满足不等式组的整数解,则这个多边形的内角和是( )A、 B、 C、 D、8. 如图,在平行四边形ABCD中,对角线AC⊥BC,M在∠CAD的平分线上,且AM⊥DM,点N为CD的中点,连接MN,若AD=12,MN=2.则AB的长为( )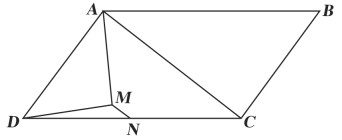 A、12 B、20 C、24 D、309. 如图,点P为定角平分线上的一个定点,且与互补.若在绕点P旋转的过程中,其两边分别与、相交于M、N两点,则以下结论中,不正确的是( )
A、12 B、20 C、24 D、309. 如图,点P为定角平分线上的一个定点,且与互补.若在绕点P旋转的过程中,其两边分别与、相交于M、N两点,则以下结论中,不正确的是( )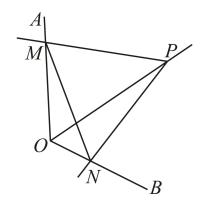 A、的值不变 B、 C、的长不变 D、四边形的面积不变10. 在平行四边形中, , 于 , 于 , , BF相交于H,BF与AD的延长线相交于点G,下面给出四个结论:①;②;③;④ , 其中正确的结论是( )
A、的值不变 B、 C、的长不变 D、四边形的面积不变10. 在平行四边形中, , 于 , 于 , , BF相交于H,BF与AD的延长线相交于点G,下面给出四个结论:①;②;③;④ , 其中正确的结论是( ) A、①②③ B、①②④ C、②③④ D、①②③④
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
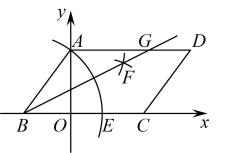
11. 若一次函数的图像经过点 , 则不等式的解集为 .12. 如图,的顶点 , ),以点B为圆心,长为半径画弧,交于点E , 分别以点A , E为圆心,以大于的长为半径画弧,两弧在的内部相交于点F , 画射线交于点G , 则点G的坐标是 .
 13. 如图第一象限内有两点 , ,将线段 平移,使点 、 分别落在两条坐标轴上,则点 平移后的对应点的坐标是.
13. 如图第一象限内有两点 , ,将线段 平移,使点 、 分别落在两条坐标轴上,则点 平移后的对应点的坐标是. 14. 我们在学习许多代数公式时,可以用几何图形来推理验证.观察图1, . 接下来,观察图2,通过类比思考,因式分解= .
14. 我们在学习许多代数公式时,可以用几何图形来推理验证.观察图1, . 接下来,观察图2,通过类比思考,因式分解= .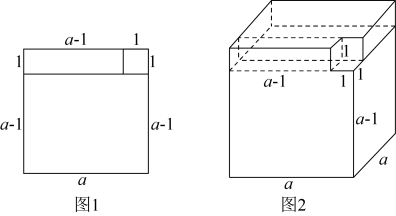 15. 如图,在和中, , , 相交于点E, . 将沿折叠,点落在点处,若 , 则的大小为 .
15. 如图,在和中, , , 相交于点E, . 将沿折叠,点落在点处,若 , 则的大小为 .
三、解答题
-
16. 按要求求解下列各题.(1)、解不等式:;(2)、解方程: .17. 先化简,再求值: , 请从不等式组的整数解中选择一个你喜欢的数求值.18. 下面是证明三角形中位线定理的两种添加辅助线的方法,选择其中一种,完成证明.
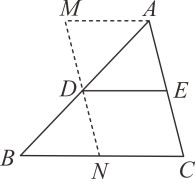
已知:如图,中,D、E分别是、的中点.

求证: , 且 .
方法一
证明:如图,延长至点F,使 , 连接 .
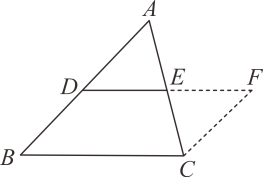
方法二
证明:如图,过点A作 , 过点D作直线交直线于M,交于N.
 19. 在中, , 尺规作图的痕迹如图所示,若 , , 求线段CD的长.
19. 在中, , 尺规作图的痕迹如图所示,若 , , 求线段CD的长.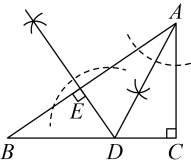 20. 某商场准备购进A,B两种书包,每个A种书包比B种书包的进价少10元,用600元购进A种书包的个数是用350元购进B种书包个数的2倍,请解答下列问题:(1)、A,B两种书包每个进价各是多少元?(2)、若该商场购进B种书包的个数比A种书包的2倍还多5个,且A种书包不少于19个,购进A,B两种书包的总费用不超过4350元,请你求出该商场有哪几种进货方案.21. 如图,各顶点的坐标分别为 , , .
20. 某商场准备购进A,B两种书包,每个A种书包比B种书包的进价少10元,用600元购进A种书包的个数是用350元购进B种书包个数的2倍,请解答下列问题:(1)、A,B两种书包每个进价各是多少元?(2)、若该商场购进B种书包的个数比A种书包的2倍还多5个,且A种书包不少于19个,购进A,B两种书包的总费用不超过4350元,请你求出该商场有哪几种进货方案.21. 如图,各顶点的坐标分别为 , , . (1)、将向上平移多少个单位,再向右平移多少个单位得到的位置?(2)、将绕点C顺时旋转得 .
(1)、将向上平移多少个单位,再向右平移多少个单位得到的位置?(2)、将绕点C顺时旋转得 .①当旋转角为时,在方格中画出;
②旋转中,当最长时,求的坐标.
22. 如图,在平行四边形中,E,F是直线上的两点, .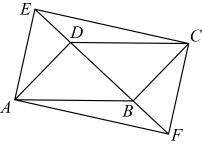 (1)、求证:四边形是平行四边形;(2)、若 , , , 且 , 求的长.23. 阅读材料:形如的式子叫做完全平方式,有些多项式虽然不是完全平方式,但可以通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.配方法在因式分解、代数最值等问题中都有广泛的应用.
(1)、求证:四边形是平行四边形;(2)、若 , , , 且 , 求的长.23. 阅读材料:形如的式子叫做完全平方式,有些多项式虽然不是完全平方式,但可以通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.配方法在因式分解、代数最值等问题中都有广泛的应用.(一)用配方法因式分解: .
解:原式
(二)用配方法求代数式的最小值.
解:原式
∵ , ∴ , ∴的最小值为 .
(1)、若代数式是完全平方式,则常数k的值为;(2)、因式分解: ;(3)、用配方法求代数式的最小值;(4)、 拓展应用:若实数a,b满足 , 则的最小值为 .
24. △ABC和△DEC是等腰直角三角形, , , .
 (1)、【观察猜想】当△ABC和△DEC按如图1所示的位置摆放,连接BD、AE,延长BD交AE于点F,猜想线段BD和AE有怎样的数量关系和位置关系.(2)、【探究证明】如图2,将△DCE绕着点C顺时针旋转一定角度 , 线段BD和线段AE的数量关系和位置关系是否仍然成立?如果成立,请证明:如果不成立,请说明理由.(3)、【拓展应用】如图3,在△ACD中, , , , 将AC绕着点C逆时针旋转90°至BC,连接BD,求BD的长.25. 如图,在平面直角坐标系xOy中,直线交x轴于点A,交y轴于点B.以AB为边作 , 点D在x轴正半轴,且 .
(1)、【观察猜想】当△ABC和△DEC按如图1所示的位置摆放,连接BD、AE,延长BD交AE于点F,猜想线段BD和AE有怎样的数量关系和位置关系.(2)、【探究证明】如图2,将△DCE绕着点C顺时针旋转一定角度 , 线段BD和线段AE的数量关系和位置关系是否仍然成立?如果成立,请证明:如果不成立,请说明理由.(3)、【拓展应用】如图3,在△ACD中, , , , 将AC绕着点C逆时针旋转90°至BC,连接BD,求BD的长.25. 如图,在平面直角坐标系xOy中,直线交x轴于点A,交y轴于点B.以AB为边作 , 点D在x轴正半轴,且 .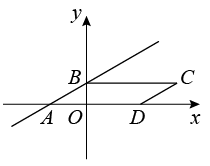
 (1)、求点C,D的坐标;(2)、点P是x轴上一点,点Q是直线CD上一点,连接BP,BQ,PQ,若是以BQ为斜边的等腰直角三角形,求点P的坐标;(3)、已知直线 , 当时,对x的每一个值都有 , 请直接写出a的取值范围.
(1)、求点C,D的坐标;(2)、点P是x轴上一点,点Q是直线CD上一点,连接BP,BQ,PQ,若是以BQ为斜边的等腰直角三角形,求点P的坐标;(3)、已知直线 , 当时,对x的每一个值都有 , 请直接写出a的取值范围.