四川省成都市天府新区2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是(　　)

A、 B、 C、 D、

查看试题解析
2. 已知 $x > y$ ，下列不等式一定成立的是（　　）

A、 $- 2 x > - 2 y$ B、 $x - 3 < y - 3$ C、 $\frac{x}{3} < \frac{y}{3}$ D、 $\frac{1}{2} x > \frac{1}{2} y$

查看试题解析
3. 已知一次函数 $y = (m + 2) x - 6$ ，若 $y$ 的值随 $x$ 值增大而减小，则m的取值范围是(　　)

A、 $m < - 2$ B、 $m > - 2$ C、 $m < 6$ D、 $- 2 < m < 6$

查看试题解析
4. 如果一个多边形的每个内角与它的外角相等，则它的边数为(　　)

A、4 B、5 C、6 D、7

查看试题解析
5. 在四边形ABCD中，AB∥CD，再添加下列其中一个条件后，四边形ABCD不一定是平行四边形的是（）

A、AB＝CD B、AD＝BC C、AD∥BC D、∠A＝∠C

查看试题解析
6. 如图， $△ A B C$ 经过平移得到 $△ D E F$ ， DE分别交BC，AC于点G，H，若 $∠ B = 97 °$ ， $∠ C = 40 °$ ，则 $∠ G H C$ 的度数为（　　）

A、147° B、40° C、97° D、43°

查看试题解析
7. 将关于 $x$ 的分式方程 $\frac{3}{x - 2} - 2 = \frac{5}{2 - x}$ 去分母后所得整式方程正确的是（　　）

A、 $3 (2 - x) - 2 (x - 2) = 5$ B、 $3 - 2 (x - 2) = - 5$ C、 $- 3 - 2 (x - 2) = 5$ D、 $3 - 2 (x - 2) = 5$

查看试题解析
8. 如图， $▱ A B C D$ 的对角线 $A C$ ， $B D$ 相交于点O，E是 $B C$ 的中点， $B E = 3$ ， $E O = 3.5$ ，则 $▱ A B C D$ 的周长为(　　)

A、 $9.5$ B、13 C、26 D、19

查看试题解析

二、填空题

9. 分解因式： $x^{2} y - 2 x y + y$ =.

查看试题解析
10. 若分式 $\frac{x}{x + 4}$ 有意义，则 $x$ 的取值范围为．

查看试题解析
11. 一次函数 $y = k x$ 和 $y = - x + 3$ 的图象如图所示，则关于x的不等式 $k x \geq - x + 3$ 的解集为．

查看试题解析
12. 如图， $△ A B C$ 是等边三角形，延长 $B C$ 到D，使 $∠ A D B = 50 °$ ，在 $A C$ 右侧作等腰直角 $△ A C E$ ， $C E$ 与 $A D$ 相交于点F，则 $∠ D A E$ 的度数为．

查看试题解析
13. 如图，在直角 $△ A B C$ 中， $∠ C = 90 °$ ，按以下步骤作图：①以点A为圆心，任意长为半径作弧，分别交 $A C$ ， $A B$ 于点E，F；②分别以E，F为圆心，大于 $\frac{1}{2} E F$ 的长为半径作弧，两弧在 $∠ B A C$ 内交于点G；③作射线 $A G$ 交 $B C$ 于点D；若 $A C = 8$ ， $B C = 6$ ，则 $C D$ 的长为．

查看试题解析

三、解答题

14.

(1)、解不等式组： ${\begin{array}{l} \frac{2 x - 1}{3} - \frac{5 x + 1}{2} \leq 1 ① \\ 5 x - 1 < 3 (x + 1) ② \end{array}$

(2)、先化简，再求值： $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x - 1}$ ，其中， $x = \sqrt{2} + 2$ ．

查看试题解析
15. 如图，在正方形网格中，每个小方格的边长为1个单位长度， $△ A B C$ 的三个顶点位置如图所示，若点A的坐标为 $(a ， 2)$ ，点B的坐标为 $(6 ， b)$ ．

(1)、在图中画出平面直角坐标系 $x O y$ ，并写出点B的坐标；

(2)、平移 $△ A B C$ ，使得点C平移到点F的位置，A，B点平移后的对应点分别是D，E，画出 $△ D E F$ ；

(3)、求 $B E$ 的长度．

查看试题解析
16. 如图，在 $▱ A B C D$ 中，对角线AC与BD相交于点O， $O F = \frac{1}{3} O A$ ， $O E = \frac{1}{3} O C$ ，连接 $B E ， B F ， D E ， D F$ ．

(1)、求证：四边形 $B E D F$ 是平行四边形；

(2)、若 $B E ⊥ A C$ ， $C E = 12$ ， $D F = 8$ ，求 $B D$ 的长．

查看试题解析
17. “成都成就梦想”，第31届世界大学生运动会将于2023年7月28日在成都举行，某特许经销商试销售A，B两类大运会纪念品，若A类纪念品每个进价比B类纪念品每个进价少5元，且用90元购进A类纪念品的数量和100元购进B类纪念品的数量相同．

(1)、求A，B两类纪念品每个进价分别是多少元？

(2)、若该经销商购进A类纪念品数量比B类纪念品数量的3倍还少5个，两类纪念品的总数不超过95个，且B类纪念品的个数多于24个，求该经销商应购进B类纪念品多少个？

查看试题解析
18. 如图，四边形 $A B C D$ 是平行四边形， $∠ D = 60 °$ ，以 $A D$ 为边向下作等边 $△ A D E$ ， F是 $A D$ 上一点， $A B = A F$ ，连接 $C F$ ，作 $∠ C F G = 60 °$ 且 $G F$ 与 $A E$ 交于点G，连接 $C G$ ．

(1)、求证： $△ A F G ≌ △ D C F$ ；

(2)、若 $∠ G C B = 45 °$ ，试判断 $C F$ ， $D E$ 的数量关系，并说明理由；

(3)、在（2）的条件下，若 $C F = \sqrt{6}$ ，求平行四边形 $A B C D$ 的面积

查看试题解析

四、填空题

19. 已知 $a + b = 3 ， a b = 2$ ，则代数式 $a^{2} b + a b^{2}$ 的值为．

查看试题解析
20. 有6张大小形状相同的卡片，正面分别写有1，2，3，4，5，6这6个数字，将它们的背面朝上洗匀后，任意抽取一张，记卡片上的数字为 $m$ ，能使关于 $x$ 的分式方程 $\frac{2 x - m}{x - 1} = 3$ 的解为正整数的概率是．

查看试题解析
21. 已知，如图， $R t △ A B C$ 面积为30， $∠ A C B = 90 °$ ， $C D$ 为 $△ A B C$ 的中线，若 $C D = \frac{13}{2}$ ，则 $△ A B C$ 的周长为．

查看试题解析
22. 我们称形如 ${\begin{array}{l} a x + b > 0 \\ b x + a > 0 \end{array}$ (其中 $\frac{b}{a}$ 为整数)的不等式组为“互倒不等式组”，若互倒不等式组 ${\begin{array}{l} a x + b > 0 \\ b x + a > 0 \end{array}$ (其中 $\frac{b}{a}$ 为整数)有且仅有1，2两个正整数解，则 $\frac{b}{a} =$ ．

查看试题解析
23. 如图，已知 $△ A B C$ 为等边三角形， $A B = 2$ ， D为 $A B$ 中点，E为直线 $B C$ 上一点，以 $D E$ 为边在 $D E$ 右侧作等边 $△ D E F$ ，连接 $A F$ ，则 $A F$ 的最小值为．

查看试题解析

五、解答题

24. 为我市创建全国文明典范城市，天府新区开展了“文明进万家·千企大联动”活动，在文明接力的同时，众多商家专门对文明市民给予特殊照顾--提供“折上折”大优惠．某商家根据近段时间的销售需求，购进甲、乙两种商品，已知按进价购买 $2$ 件甲商品与 $3$ 件乙商品费用为 $180$ 元，按进价购买 $3$ 件甲商品的费用比 $2$ 件乙商品的费用多 $75$ 元．

(1)、求甲乙商品每件的进价各是多少元；

(2)、商家准备购进甲乙两种商品共 $300$ 件，且甲商品件数的 $3$ 倍不低于乙商品件数．甲乙商品的原售价分别为 $62$ 元 $/$ 件， $50$ 元 $/$ 件，现做以下优惠活动：甲商品销售单价降低 $9$ 元，乙商品打八折售价，若 $300$ 件商品全部卖完，则该商家的总利润 $W$ 最大是多少元？

查看试题解析
25. 如图，直线 $y = x + 2$ 与坐标轴交于A，B两点，点C坐标为 $(\frac{11}{2} ， 0)$ ，将B点向右平移4个单位，再向下平移1个单位得到点D，直线 $C D$ 交直线 $A B$ 于点E．

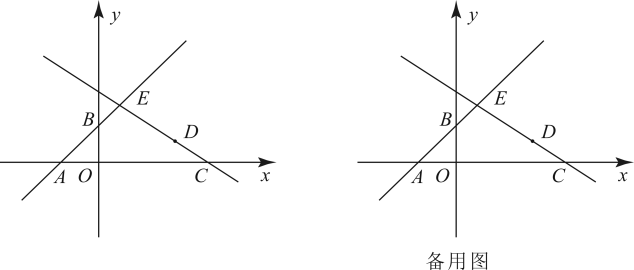(1)、求直线 $C D$ 的表达式；

(2)、我们定义：如果一个三角形中有一个内角为 $45 °$ ，则称这个三角形为“天府三角形”
①点F是直线 $A B$ 上第一象限内一点，若 $△ E F D$ 为“天府三角形”，求点F的坐标；

②在①的条件下，当点F的横坐标大于 $\frac{7}{2}$ 时，作点B关于x轴的对称点 $B^{'}$ ，点P为直线 $F D$ 上的一个动点，连接 $A P$ ，点Q为线段 $A P$ 的中点，连接 $B^{'} Q$ ，当 $A P + 2 B^{'} Q$ 最小时，求点Q的坐标．

查看试题解析
26. 在等腰直角 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = \sqrt{2}$ ，将直角边AC绕点A顺时针旋转得到AP，旋转角为 $α (0 ° < α < 180 °)$ ，连接CP，PB．

(1)、如图1，当 $α = 45 °$ 时，求BP的长；

(2)、如图2，若 $∠ C P B = 135 °$ ，且D为AB中点，连接PD，猜想CP和DP的数量关系，并说明理由；

(3)、在旋转过程中，当 $C P = B P$ 时，求旋转角 $α$ 的度数．

查看试题解析