四川省广安市邻水县2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 若二次根式在实数范围内有意义,则的取值范围是( )A、 B、 C、 D、2. 下列各曲线中,不能表示是的函数的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在四边形中,两组对边分别相等.若 , 则的度数为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. “杂交水稻之父”袁隆平培育的超级杂交稻在全世界推广种植.某种植户为了考察所种植的杂交水稻苗的长势,从稻田中随机抽取了9株水稻苗,测得苗高(单位:)分别是21,23,22,23,24,25,24,23,25.则这组数据的众数和中位数分别是( )A、23,23 B、23,24 C、24,25 D、24,246. 在中, , , 的对边分别记为a,b,c,由下列条件不能判定为直角三角形的是( )A、 B、 C、 D、7. 如图是一支温度计的示意图,图中左边是用摄氏温度表示的温度值,右边是用华氏温度表示的温度值,下表是这两个温度值之间的部分对应关系:
3. 在四边形中,两组对边分别相等.若 , 则的度数为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. “杂交水稻之父”袁隆平培育的超级杂交稻在全世界推广种植.某种植户为了考察所种植的杂交水稻苗的长势,从稻田中随机抽取了9株水稻苗,测得苗高(单位:)分别是21,23,22,23,24,25,24,23,25.则这组数据的众数和中位数分别是( )A、23,23 B、23,24 C、24,25 D、24,246. 在中, , , 的对边分别记为a,b,c,由下列条件不能判定为直角三角形的是( )A、 B、 C、 D、7. 如图是一支温度计的示意图,图中左边是用摄氏温度表示的温度值,右边是用华氏温度表示的温度值,下表是这两个温度值之间的部分对应关系:摄氏温度值x/℃
0
10
20
30
40
50
华氏温度值y/℉
32
50
68
86
104
122
 根据以上信息,可以得到y与x之间的关系式为( )A、 B、 C、 D、8. 下列说法正确的是( )A、对角线互相垂直的四边形是菱形 B、四条边都相等的四边形是正方形 C、直角三角形斜边上的中线等于斜边的一半 D、有一组对边相等,一组对边平行的四边形是平行四边形9. 关于x的一次函数 , 下列说法错误的是( )A、若函数的图象经过原点,则 B、当时,y随x的增大而减小 C、函数的图象一定经过点 D、若函数的图象经过第一、三、四象限,则k的取值范围是10. 如图,中, , , . 以 , 为直角边,构造;再以 , 为直角边,构造;……,按照这个规律,在中,点到的距离是( )
根据以上信息,可以得到y与x之间的关系式为( )A、 B、 C、 D、8. 下列说法正确的是( )A、对角线互相垂直的四边形是菱形 B、四条边都相等的四边形是正方形 C、直角三角形斜边上的中线等于斜边的一半 D、有一组对边相等,一组对边平行的四边形是平行四边形9. 关于x的一次函数 , 下列说法错误的是( )A、若函数的图象经过原点,则 B、当时,y随x的增大而减小 C、函数的图象一定经过点 D、若函数的图象经过第一、三、四象限,则k的取值范围是10. 如图,中, , , . 以 , 为直角边,构造;再以 , 为直角边,构造;……,按照这个规律,在中,点到的距离是( )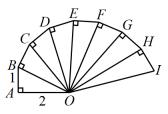 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 甲、乙两名同学投掷实心球,每人投10次,平均成绩都为 , 方差分别为 , , 则成绩比较稳定的是同学.(填“甲”或“乙”)12. 已知一次函数的图象经过点和 , 当函数值时,x的取值范围为 .13. 已知实数a满足 , 则的值为 .14. 如图,已知的周长是 , 对角线和相交于点 , 的周长比的周长大 , 则 .
 15. 如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是。
15. 如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是。 16. 如图,在△ABC中,DE∥CA,DF∥BA,下列说法:①如果∠BAC=90°,那么四边形AEDF是矩形;②如果AD平分∠BAC,那么四边形AEDF是菱形;③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形.其中正确的有个
16. 如图,在△ABC中,DE∥CA,DF∥BA,下列说法:①如果∠BAC=90°,那么四边形AEDF是矩形;②如果AD平分∠BAC,那么四边形AEDF是菱形;③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形.其中正确的有个
三、解答题
-
17. 计算: .18. 观察下列各组勾股数有哪些规律:
3,4,5
5,12,13
7,24,25
9,40,41
……
a,b,c
请解答:
(1)、当a=11时,求b,c的值;(2)、判断21,220,221是否为一组勾股数?若是,请说明理由.19. 如图,正比例函数的图象经过点 . (1)、求k的值;(2)、请在如图所示的平面直角坐标系中画出一次函数的图象;(3)、根据图象,直接写出关于x的不等式的取值范围是 .20. 如图,在中, , D、E、F分别是边的中点,求证:四边形是菱形.
(1)、求k的值;(2)、请在如图所示的平面直角坐标系中画出一次函数的图象;(3)、根据图象,直接写出关于x的不等式的取值范围是 .20. 如图,在中, , D、E、F分别是边的中点,求证:四边形是菱形. 21. 为深入学习贯彻习近平法治思想,推动青少年宪法学习宣传教育走深走实,某校开展了宪法知识在线学习、知识竞赛与演讲比赛三项活动,下表是参加冠亚军决赛的两名选手的各项测试成绩(单位:分).
21. 为深入学习贯彻习近平法治思想,推动青少年宪法学习宣传教育走深走实,某校开展了宪法知识在线学习、知识竞赛与演讲比赛三项活动,下表是参加冠亚军决赛的两名选手的各项测试成绩(单位:分).选手/项目
在线学习
知识竞赛
演讲比赛
甲
84
96
90
乙
89
99
85
(1)、若将在线学习、知识竞赛与演讲比赛三项成绩的平均分作为最后成组,谁将获得冠军?(2)、若将在线学习、知识竞赛与演讲比赛的成绩按2:3:5的比例计算最后成绩,谁将获得冠军?22. 台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿AB由点A向点B移动,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域. (1)、海港C受台风影响吗?为什么?(2)、若台风的速度为25km/h,台风影响该海港持续的时间有多长?23. 某店销售甲、乙两种特价商品,两种商品的进价与售价如表所示:
(1)、海港C受台风影响吗?为什么?(2)、若台风的速度为25km/h,台风影响该海港持续的时间有多长?23. 某店销售甲、乙两种特价商品,两种商品的进价与售价如表所示:甲商品
乙商品
进价(元/件)
35
5
售价(元/件)
45
8
该店计划购进甲、乙两种商品共100件进行销售,设购进甲商品x件,甲、乙两种商品全部销售完后获得的利润为y元.
(1)、求出y与x之间的函数关系式;(2)、若购进乙商品的件数不少于甲商品件数的3倍,当购进甲、乙两种商品各多少件时,可使得甲、乙两种商品全部销售完后获得的利润最大?最大利润是多少?24. 某居民小区有块形状为长方形ABCD的绿地,长方形绿地的长BC为 米,宽AB为 米,现要在长方形绿地中修建一个长方形花坛(即图中阴影部分),长方形花坛的长为 米,宽为 米. (1)、长方形ABCD的周长是多少?(结果化为最简二次根式)(2)、除去修建花坛的地方,其它地方全修建成通道,通道上要铺上造价为6元/ 的地砖,要铺完整个通道,则购买地砖需要花费多少元?(结果化为最简二次根式)25. 阅读下列内容:设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三边长之间的关系来判断这个三角形的形状:①若 , 则该三角形是直角三角形;②若 , 则该三角形是钝角三角形;③若 , 则该三角形是锐角三角形.例如:若一个三角形的三边长分别是4,5,6,则最长边是6,由于 , 故由上面的③可知该三角形是锐角三角形.请解答以下问题:(1)、若一个三角形的三边的长分别是6,7,8,则该三角形的形状是三角形.(2)、若一个三角形的三边的长分别是5,12,x,且这个三角形是直角三角形,求x的值.(3)、若一个三角形的三条边的长分别是 , , , 请判断这个三角形的形状,并写出你的判断过程.26. 已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.(1)、如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(1)、长方形ABCD的周长是多少?(结果化为最简二次根式)(2)、除去修建花坛的地方,其它地方全修建成通道,通道上要铺上造价为6元/ 的地砖,要铺完整个通道,则购买地砖需要花费多少元?(结果化为最简二次根式)25. 阅读下列内容:设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三边长之间的关系来判断这个三角形的形状:①若 , 则该三角形是直角三角形;②若 , 则该三角形是钝角三角形;③若 , 则该三角形是锐角三角形.例如:若一个三角形的三边长分别是4,5,6,则最长边是6,由于 , 故由上面的③可知该三角形是锐角三角形.请解答以下问题:(1)、若一个三角形的三边的长分别是6,7,8,则该三角形的形状是三角形.(2)、若一个三角形的三边的长分别是5,12,x,且这个三角形是直角三角形,求x的值.(3)、若一个三角形的三条边的长分别是 , , , 请判断这个三角形的形状,并写出你的判断过程.26. 已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.(1)、如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;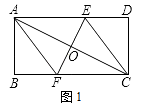 (2)、如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
(2)、如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.