四川省眉山市2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 要使分式 $\frac{x - 3}{x + 5}$ 有意义，则 $x$ 的取值应该满足(　　)

A、 $x \neq - 5$ B、 $x \neq 5$ C、 $x = 3$ D、 $x \neq 0$

查看试题解析
2. 每年10月16日为世界粮食日，它告诫人们要珍惜每一粒粮食．已知一粒米的重量约0.000 021千克，将数据0.000 021用科学记数法表示为（）

A、 $0.21 \times 1 0^{- 4}$ B、 $2.1 \times 1 0^{- 4}$ C、 $2.1 \times 1 0^{- 5}$ D、 $21 \times 1 0^{- 6}$

查看试题解析
3. 一次函数 $y = (k - 3) x + 2$ 的函数值 $y$ 随 $x$ 的增大而减小，则 $k$ 的值为（）

A、2 B、3 C、4 D、5

查看试题解析
4. 下列结论中，不正确的是（　　）

A、对角线互相垂直的平行四边形是菱形 B、对角线相等的平行四边形是矩形 C、对角线互相垂直平分的四边形是正方形 D、一组对边平行且相等的四边形是平行四边形

查看试题解析
5. 在学校开展的“弘扬东坡文化，砥砺前行之志”的一次演讲比赛中，编号分别为1，2，3，4，5五位同学最后成绩如表所示：
参赛者编号
1
2
3
4
5
成绩（分）
97
88
85
93
85
那么这五位同学演讲成绩的众数与中位数依次是（　　）

A、97，85 B、95，88 C、85，85 D、85，88

查看试题解析
6. 关于x的方程 $\frac{3 x - 1}{x - 3} = \frac{a}{3 - x} - 1$ 有增根，则a的值是（　　）

A、3 B、8 C、 $- 8$ D、 $- 14$

查看试题解析
7. 直线 $y = k x + b$ 与直线 $y = - 4 x + 2023$ 平行，且与y轴交于点 $P (0 ， - 5)$ ，则其函数表达式是（　　）

A、 $y = 4 x + 2023$ B、 $y = - 4 x - 5$ C、 $y = 4 x + 5$ D、 $y = - 4 x - 2023$

查看试题解析
8. 如图，矩形纸片 $A B C D$ 中 $A B = 2$ ， $B C = 4$ ，将 $△ A B C$ 沿 $A C$ 折叠，使点 $B$ 落在点 $E$ 处， $C E$ 交 $A D$ 于点 $F$ ，则 $△ C D F$ 的面积等于(　　)

A、 $\frac{3}{2}$ B、 $\frac{4}{3}$ C、3 D、 $\frac{2}{3}$

查看试题解析
9. 如图，在 $▱ A B C D$ 中，E为 $C D$ 边上一点，且 $B E = B C ， ∠ C = 55 ° ， ∠ E B D = 25 °$ ， $∠ A E B$ 的度数为（　　）

A、 $90 °$ B、 $95 °$ C、 $100 °$ D、 $105 °$

查看试题解析
10. 如图，点B在y轴的正半轴上，点C在反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象上，菱形 $O A B C$ 的面积为8，则k的值为（）

A、 $- 4$ B、4 C、 $- 2$ D、2

查看试题解析
11. 如图，正比例函数 $y = k_{1} x$ 与反比例函数 $y = \frac{k_{2}}{x}$ 的图象交于 $A (3 ， a)$ 、 $B$ 两点，当 $k_{1} x \leq \frac{k_{2}}{x}$ 时， $x$ 的取值范围是(　　)

A、 $x \leq - 3$ 或 $0 < x \leq 3$ B、 $- 3 \leq x < 0$ 或 $0 < x \leq 3$ C、 $x \leq - 3$ 或 $x \geq 3$ D、 $- 3 \leq x < 0$ 或 $x \geq 3$

查看试题解析
12. 如图，在正方形 $A B C D$ 中，E为对角线AC上一点，连接 $D E$ ，过点E作 $E F ⊥ D E$ ，交BC延长线于点F，以 $D E ， E F$ 为邻边作矩形 $D E F G$ ，连接 $C G$ ．在下列结论中：
① $E D = E F$ ；
② $A E = C G$ ；
③ $A E ⊥ C G$ ；
④ $∠ D E C = ∠ C F G$ ．
其中正确结论的个数是（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 计算 ${(\sqrt{3} - 1)}^{0} - {(- \frac{1}{3})}^{- 2} =$ ．

查看试题解析
14. 甲、乙两名射击手的 $10$ 次测试的平均成绩都是 $8$ 环，方差分别是 $S_{甲}^{2} = 2.4$ （环 $^{2}$ ）， $S_{乙}^{2} = 3.5$ （环 $^{2}$ ），则成绩比较稳定的射击手是（填甲或乙）．

查看试题解析
15. 在坐标平面内，已知正比例函数 $y = 2 x$ 与一次函数 $y = x - 1$ 的图象交于点A，则点A的坐标为．

查看试题解析
16. 如图，在矩形ABCD中， $B C = 4$ ，对角线AC与BD相交于点O， $A N ⊥ B D$ ，垂足为N， $B N = 3 D N$ ，则AN长为.

查看试题解析
17. 如图，四边形 $A B C D$ 为菱形， $∠ A B C = 76 °$ ，延长 $B C$ 到 $E$ ，在 $∠ D C E$ 内作射线 $C M$ ，使得 $∠ E C M = 24 °$ ，过点 $D$ 作 $D F ⊥ C M$ ，垂足为 $F$ ，若 $D F = 8$ ，则对角线 $B D$ 的长为．

查看试题解析
18. 如图，已知点A是一次函数 $y = \frac{1}{2} x (x \geq 0)$ 图象上一点，过点A作x轴的垂线l，点B是l上一点（点B在点A上方），在 $A B$ 的右侧以线段 $A B$ 为斜边作等腰直角三角形 $A B C$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象过点B，C，若 $△ O A B$ 的面积为8，则k的值为．

查看试题解析

三、解答题

19. 解方程： $\frac{x - 6}{x - 5} - 2 = \frac{1}{5 - x}$ ．

查看试题解析
20. 如图，在平行四边形 $A B C D$ 中，对角线 $A C ， B D$ 相交于点O，过点O的直线 $E F$ 分别交 $A D$ 于点E，交 $B C$ 于点F，求证： $A E = C F$ ．

查看试题解析
21. 先化简，再求值： $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4}{x^{2} - 2 x + 1}$ ，其中 $x = 4$ ．

查看试题解析

22. 2023年“五•一”期间上映《长空之王》和《惊天救援》两部影片．《长空之王》演绎了新一代试飞员在挫折中成长，最终成为优秀试飞员的励志故事；《惊天救援》讲述了消防员在危难时刻争分夺秒，用生命守护生命的感人故事．为了解中学生对这两影片的喜爱程度，某调查小组从该校八年级学生中随机抽取了10名学生对这两部影片分别进行打分（满分10分），其中《长空之王》得分为：9，6，9，7，8，9，6，8，9，9，根据打分制作了如下两幅图表．

抽取的学生对两部影片打分的统计量

统计量

影片

平均数

众数

中位数

《长空之王》

《惊天救援》

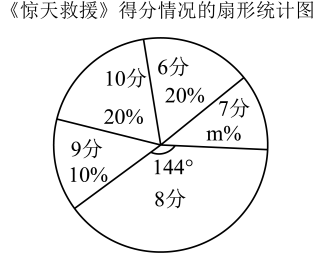
请根据以上信息，解答下列问题：

(1)、上述图表中，

a =

，

b =

，

c =

，

m =

．

(2)、根据以上数据，你认为该校八年级学生更喜爱哪部影片？请说明理由（写出一条理由即可）．

查看试题解析

23. 为打造“天府粮仓”，守住耕地红线，某市第一批计划退林还耕1500亩．对外招标，从投标书中得知：甲队每天退林还耕的亩数是乙队的1.2倍；单独完成退林还耕甲队比乙队少用5天．求甲、乙两队每天完成退林还耕多少亩？

查看试题解析
24. 如图，在平面直角坐标系中，直线 $y = - \frac{1}{3} x + 3$ 与x轴、y轴分别交于F，E两点，与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象交于点 $A (3 ， a)$ 和点 $B (6 ， b)$ ．

(1)、求反比例函数解析式和B点坐标；

(2)、如图，连接 $O A$ ， P为线段 $O F$ 上一点，使得 $S_{△ P A B} = \frac{5}{9} S_{△ O A E}$ ，求P点坐标．

查看试题解析
25. 如图，菱形 $O A B C$ 的一边 $O C$ 在x轴的正半轴上，O是坐标原点，B点坐标为 $(8 ， 4)$ ，点D是对角线 $O B$ 上一点，连结 $D A ， D C ， A E ⊥ O C$ ，垂足为E．

(1)、求证： $D A = D C$ ；

(2)、求菱形 $O A B C$ 的面积；

(3)、连接 $D E$ ，当 $S_{△ D A E} = 2$ 时，求点D的坐标．

查看试题解析
26. 四边形 $A B C D$ 和四边形 $B F D E$ 都是矩形， $B C$ 与 $D F$ 交于点 $G$ ， $A D$ 与 $B E$ 交于点 $H$ ．

(1)、如图1，当 $A B = B F$ 时，求证： $B H = D H$ ；

(2)、如图2，当 $A B = B F$ 时，连结 $C H$ ，若 $B C = 2 A B$ ，求 $\frac{C H}{C D}$ 的值；

(3)、如图3，当 $A B \neq B F$ 时，连结 $C H$ ， $G H$ ，若 $△ C G H$ 为等边三角形，求 $\frac{A B}{B F}$ 的值．

查看试题解析

参赛者编号	1	2	3	4	5
成绩（分）	97	88	85	93	85