四川省泸州市泸县2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、3. 如图,在中, , 是的平分线,若 , 则等于( )
2. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、3. 如图,在中, , 是的平分线,若 , 则等于( )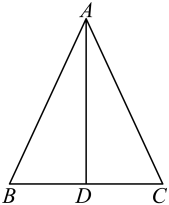 A、3 B、4 C、5 D、64. 下列运算正确的是( )A、 B、 C、 D、5. 如图, , 点C是内一点,于点D,于点E.且 , 则的度数是( )
A、3 B、4 C、5 D、64. 下列运算正确的是( )A、 B、 C、 D、5. 如图, , 点C是内一点,于点D,于点E.且 , 则的度数是( ) A、 B、 C、 D、6. 某组8名男生在中考体育测试中引体向上个数分别为:6,8,7,7,8,9,8,9.则这组数据的中位数和众数分别是( )A、 , 7 B、 , 8 C、8,7 D、8,87. 已知一次函数 , 则满足的x的取值范围是( )A、 B、 C、 D、8. 下列命题中正确的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相垂直且相等的四边形是正方形 D、一组对边平行且相等的四边形是平行四边形9. 小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系,根据图象,下列信息错误的是( )
A、 B、 C、 D、6. 某组8名男生在中考体育测试中引体向上个数分别为:6,8,7,7,8,9,8,9.则这组数据的中位数和众数分别是( )A、 , 7 B、 , 8 C、8,7 D、8,87. 已知一次函数 , 则满足的x的取值范围是( )A、 B、 C、 D、8. 下列命题中正确的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相垂直且相等的四边形是正方形 D、一组对边平行且相等的四边形是平行四边形9. 小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系,根据图象,下列信息错误的是( ) A、小明看报用时8分钟 B、公共阅报栏距小明家200米 C、小明离家最远的距离为400米 D、小明从出发到回家共用时16分钟10. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若 , 大正方形的面积为13,则小正方形的面积为( )
A、小明看报用时8分钟 B、公共阅报栏距小明家200米 C、小明离家最远的距离为400米 D、小明从出发到回家共用时16分钟10. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若 , 大正方形的面积为13,则小正方形的面积为( )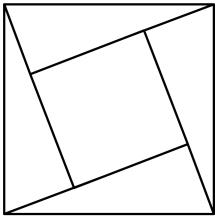 A、3 B、4 C、5 D、611. 已知点 , , 都在直线上,则 , , 的大小关系正确的是( )A、 B、 C、 D、12. 如图,与是等腰直角三角形, , A,E,D在一条直线上, . 若 , , 则的长为( )
A、3 B、4 C、5 D、611. 已知点 , , 都在直线上,则 , , 的大小关系正确的是( )A、 B、 C、 D、12. 如图,与是等腰直角三角形, , A,E,D在一条直线上, . 若 , , 则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 分解因式: =.
14. 要使有意义,则的取值范围是 .15. 一个多边形的内角和是720°,这个多边形的边数是 .16. 如图,在矩形中, , , 点E是的中点,将沿折叠,使顶点C落在矩形内的点F处,连接、则的长为 .
三、解答题
-
17. .18. 计算: .19. 化简: .20. 如图,已知线段、相交于点O, , . 求证: .
 21. 某中学为了解学生参加户外活动的情况,随机调查了该校部分学生每周参加户外活动的时间,并用得到的数据绘制了如下两幅不完整的统计图.
21. 某中学为了解学生参加户外活动的情况,随机调查了该校部分学生每周参加户外活动的时间,并用得到的数据绘制了如下两幅不完整的统计图.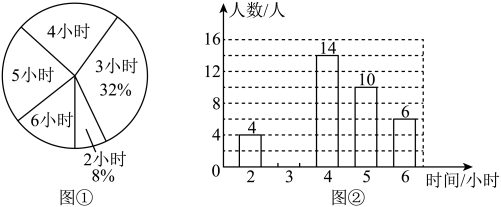
请根据以上信息,解答下列问题:
(1)、这次调查的学生共人;(2)、补全条形统计图;(3)、若该校共有1500名学生,估计该校参加户外活动时间超过3小时的学生人数.22. 如图,某学校矩形停车位边上有一块空地(阴影部分)需要绿化.测得 , , , , 求需要绿化部分(阴影部分)的面积.