山东省泰安市2023年中考数学真题

试卷更新日期：2023-07-26 类型：中考真卷

进入出卷网下载

一、单选题

1. $- \frac{2}{3}$ 的倒数是（）

A、 $\frac{2}{3}$ B、 $- \frac{2}{3}$ C、 $\frac{3}{2}$ D、 $- \frac{3}{2}$

查看试题解析
2. 下列运算正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 $(a - b)^{2} = a^{2} - b^{2}$ C、 ${(a b^{2})}^{3} = a^{3} b^{5}$ D、 $3 a^{3} \cdot (- 4 a^{2}) = - 12 a^{5}$

查看试题解析
3. 2023年1月17日，国家航天局公布了我国嫦娥五号月球样品的科研成果．科学家们通过对月球样品的研究，精确测定了月球的年龄是 $20.3$ 亿年，数据 $20.3$ 亿年用科学记数法表示为（）

A、 $2.03 \times 1 0^{8}$ 年 B、 $2.03 \times 1 0^{9}$ 年 C、 $2.03 \times 1 0^{10}$ 年 D、 $20.3 \times 1 0^{9}$ 年

查看试题解析
4. 小亮以四种不同的方式连接正六边形的两条对角线，得到如下四种图形，则既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 把一块直角三角板和一把直尺如图放置，若 $∠ 1 = 35 °$ ，则 $∠ 2$ 的度数等于（）

A、 $65 °$ B、 $55 °$ C、 $45 °$ D、 $60 °$

查看试题解析
6. 为了解学生的身体素质状况，国家每年都会进行中小学生身体素质抽测．在今年的抽测中，某校九年级二班随机抽取了 $10$ 名男生进行引体向上测试，他们的成绩（单位：个）如下： $7$ ， $11$ ， $10$ ， $11$ ， $6$ ， $14$ ， $11$ ， $10$ ， $11$ ， $9$ ．根据这组数据判断下列结论中错误的是（）

A、这组数据的众数是 $11$ B、这组数据的中位数是 $10$ C、这组数据的平均数是 $10$ D、这组数据的方差是 $4.6$

查看试题解析
7. 如图， $A B$ 是 $⊙ O$ 的直径，D，C是 $⊙ O$ 上的点， $∠ A D C = 115 °$ ，则 $∠ B A C$ 的度数是（）

A、 $25 °$ B、 $30 °$ C、 $35 °$ D、 $40 °$

查看试题解析
8. 一次函数 $y = a x + b$ 与反比例函数 $y = \frac{a b}{x}$ （a，b为常数且均不等于0）在同一坐标系内的图象可能是（）

A、 B、 C、 D、

查看试题解析
9. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆，半径为4，连接OB，OC，OA，若 $∠ C A O = 40 °$ ， $∠ A C B = 70 °$ ，则阴影部分的面积是（）

A、 $\frac{4}{3} π$ B、 $\frac{8}{3} π$ C、 $\frac{16}{3} π$ D、 $\frac{32}{3} π$

查看试题解析
10. 《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等，交易其一，金轻十三两，问金、银各重几何？”意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等，两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计），问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两．根据题意得（）

A、 ${\begin{array}{l} 11 x = 9 y ， \\ (10 y + x) - (8 x + y) = 13 ． \end{array}$ B、 ${\begin{array}{l} 10 y + x = 8 x + y ， \\ 9 x + 13 = 11 y ． \end{array}$ C、 ${\begin{array}{l} 9 x = 11 y ， \\ (10 y + x) - (8 x + y) = 13 ． \end{array}$ D、 ${\begin{array}{l} 9 x = 11 y \\ (8 x + y) - (10 y + x) = 13 ． \end{array}$

查看试题解析
11. 如图， $△ A B C$ 是等腰三角形， $A B = A C ， ∠ A = 36 °$ ．以点B为圆心，任意长为半径作弧，交AB于点F，交BC于点G，分别以点F和点G为圆心，大于 $\frac{1}{2} F G$ 的长为半径作弧，两弧相交于点H，作射线BH交AC于点D；分别以点B和点D为圆心，大于 $\frac{1}{2} B D$ 的长为半径作弧，两孤相交于M、N两点，作直线MN交AB于点E，连接DE．下列四个结论：① $∠ A E D = ∠ A B C$ ；② $B C = A E$ ；③ $E D = \frac{1}{2} B C$ ；④当 $A C = 2$ 时， $A D = \sqrt{5} - 1$ ．其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
12. 如图，在平面直角坐标系中， $R t △ A O B$ 的一条直角边 $O B$ 在x轴上，点A的坐标为 $(- 6 ， 4)$ ； $R t △ C O D$ 中， $∠ C O D = 90 ° ， O D = 4 \sqrt{3} ， ∠ D = 30 °$ ，连接 $B C$ ，点M是 $B C$ 中点，连接 $A M$ ．将 $R t △ C O D$ 以点O为旋转中心按顺时针方向旋转，在旋转过程中，线段 $A M$ 的最小值是（）

A、3 B、 $6 \sqrt{2} - 4$ C、 $2 \sqrt{13} - 2$ D、2

查看试题解析

二、填空题

13. 已知关于x的一元二次方程 $x^{2} - 4 x - a = 0$ 有两个不相等的实数根，则a的取值范围是．

查看试题解析
14. 为了测量一个圆形光盘的半径，小明把直尺、光盘和三角尺按图所示放置于桌面上，并量出 $A B = 4 c m$ ，则这张光盘的半径是 $c m$ ．（精确到 $0.1 c m$ ．参考数据： $\sqrt{3} \approx 1 ． 73$ ）

查看试题解析
15. 二次函数 $y = - x^{2} - 3 x + 4$ 的最大值是．

查看试题解析
16. 在一次综合实践活动中，某学校数学兴趣小组对一电视发射塔的高度进行了测量．如图，在塔前C处，测得该塔顶端B的仰角为 $50 °$ ，后退 $60 m$ （ $C D = 60 m$ ）到D处有一平台，在高 $2 m$ （ $D E = 2 m$ ）的平台上的E处，测得B的仰角为 $26.6 °$ ．则该电视发射塔的高度 $A B$ 为 $m$ ．（精确到 $1 m$ ．参考数据： $t a n 50 ° \approx 1.2 ， t a n 26.6 ° \approx 0.5$ ）

查看试题解析
17. 如图，在 $△ A B C$ 中， $A C = B C = 16$ ，点D在 $A B$ 上，点E在 $B C$ 上，点B关于直线 $D E$ 的轴对称点为点 $B^{'}$ ，连接 $D B^{'}$ ， $E B^{'}$ ，分别与 $A C$ 相交于F点，G点，若 $A F = 8 ， D F = 7 ， B^{'} F = 4$ ，则 $C G$ 的长度为．

查看试题解析
18. 已知， $△ O A_{1} A_{2} ， △ A_{3} A_{4} A_{5} ， △ A_{6} A_{7} A_{8} ， ⋯ ⋯$ 都是边长为2的等边三角形，按下图所示摆放．点 $A_{2} ， A_{3} ， A_{5} ， ⋯ ⋯$ 都在x轴正半轴上，且 $A_{2} A_{3} = A_{5} A_{6} = A_{8} A_{9} = ⋯ ⋯ = 1$ ，则点 $A_{2023}$ 的坐标是．

查看试题解析

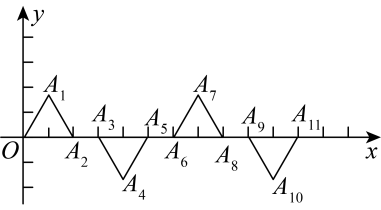
三、解答题

19.

(1)、化简： $(2 - \frac{x - 1}{x + 2}) \div \frac{x^{2} + 10 x + 25}{x^{2} - 4}$ ；

(2)、解不等式组： ${\begin{array}{l} 2 x + 7 > 3 \\ \frac{x + 1}{3} > \frac{x - 1}{2} \end{array}$ ．

查看试题解析
20. 2022年10月16日至10月22日，中国共产党第二十次全国代表大会在北京召开．为激励青少年争做党的事业接班人，某市团市委在党史馆组织了“红心永向党”为主题的知识竞赛，依据得分情况将获奖结果分为四个等级：A级为特等奖，B级为一等奖，C级为二等奖，D级为优秀奖．并将统计结果绘制成了如图所示的两幅不完整的统计图．

请根据相关信息解答下列问题：

(1)、本次竞赛共有名选手获奖，扇形统计图中扇形C的圆心角度数是度；

(2)、补全条形统计图；

(3)、若该党史馆有一个入口，三个出口．请用树状图或列表法，求参赛选手小丽和小颖由馆内恰好从同一出口走出的概率．

查看试题解析
21. 如图，一次函数 $y_{1} = - 2 x + 2$ 的图象与反比例函数 $y_{2} = \frac{k}{x}$ 的图象分别交于点 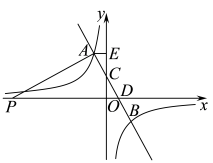$A$ ，点 $B$ ，与 $y$ 轴， $x$ 轴分别交于点 $C$ ，点 $D$ ，作 $A E ⊥ y$ 轴，垂足为点 $E$ ， $O E = 4$ ．

(1)、求反比例函数的表达式；

(2)、在第二象限内，当 $y_{1} < y_{2}$ 时，直接写出 $x$ 的取值范围；

(3)、点 $P$ 在 $x$ 轴负半轴上，连接 $P A$ ，且 $P A ⊥ A B$ ，求点 $P$ 坐标．

查看试题解析
22. 为进行某项数学综合与实践活动，小明到一个批发兼零售的商店购买所需工具．该商店规定一次性购买该工具达到一定数量后可以按批发价付款，否则按零售价付款．小明如果给学校九年级学生每人购买一个，只能按零售价付款，需用3600元；如果多购买60个，则可以按批发价付款，同样需用3600元，若按批发价购买60个与按零售价购买50个所付款相同，求这个学校九年级学生有多少人？

查看试题解析
23. 如图，矩形 $A B C D$ 中，对角线 $A C ， B D$ 相交于点O，点F是 $D C$ 边上的一点，连接 $A F$ ，将 $△ A D F$ 沿直线 $A F$ 折叠，点D落在点G处，连接 $A G$ 并延长交 $D C$ 于点H，连接 $F G$ 并延长交 $B C$ 于点M，交 $A B$ 的延长线于点E，且 $A C = A E$ ．

(1)、求证：四边形 $D B E F$ 是平行四边形；

(2)、求证： $F H = M E$ ．

查看试题解析
24. 如图， $△ A B C$ 、 $△ C D E$ 是两个等腰直角三角形， $E F ⊥ A D$ ．

(1)、当 $A F = D F$ 时，求 $∠ A E D$ ；

(2)、求证： $△ E H G ∽ △ A D G$ ；

(3)、求证： $\frac{A E}{E H} = \frac{A C}{H C}$ ．

查看试题解析
25. 如图1，二次函数 $y = a x^{2} + b x + 4$ 的图象经过点 $A (- 4 ， 0) ， B (- 1 ， 0)$ ．

(1)、求二次函数的表达式；

(2)、若点P在二次函数对称轴上，当 $△ B C P$ 面积为5时，求P坐标；

(3)、小明认为，在第三象限抛物线上有一点D，使 $∠ D A B + ∠ A C B = 90 °$ ；请判断小明的说法是否正确，如果正确，请求出D的坐标；如果不正确，请说明理由．

查看试题解析