北京市石景山区2022—2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 太钢不锈钢精密带钢有限公司生产的“手撕钢”宽 $0.6$ 米、厚 $0.000015$ 米（ $0.015$ 毫米），广泛应用于航空航天、新能源、 $5 G$ 通信等高精尖端设备制造行业，至今保持世界最宽、最薄“手撕钢”记录． $0.000015$ 用科学记数法表示应为（）

A、 $1.5 \times 1 0^{5}$ B、 $1.5 \times 1 0^{- 5}$ C、 $1.5 \times 1 0^{- 6}$ D、 $1.5 \times 1 0^{- 7}$

查看试题解析
2. 下列运算正确的是（）

A、 $2 a + 3 a^{2} = 5 a^{3}$ B、 ${(- a^{3})}^{2} = a^{6}$ C、 $- 4 a^{3} b \div 2 a = - 2 a^{2}$ D、 ${(5 a b)}^{2} = 10 a^{2} b^{2}$

查看试题解析
3. 以下调查中，适合用全面调查的是（）

A、了解一批科学计算器的使用寿命 B、调查北京市中学生对神舟十六号载人飞行任务标识寓意的了解情况 C、了解某班同学登上八达岭长城的人数情况 D、调查市场上某种食品的色素含量是否符合国家标准

查看试题解析
4. 下列因式分解正确的是（）

A、 $x^{2} y - y^{3} = y {(x - y)}^{2}$ B、 $m^{2} - 6 m - 9 = {(m - 3)}^{2}$ C、 $x^{2} + x - 1 = x (x + 1) - 1$ D、 $x^{2} - 2 x y + x = x (x - 2 y + 1)$

查看试题解析
5. 如图，下列条件中，能判断 $A D ∥ B C$ 的是（）

A、 $∠ 3 = ∠ 4$ B、 $∠ 1 = ∠ 2$ C、 $∠ 5 = ∠ C$ D、 $∠ A + ∠ A D C = 180 °$

查看试题解析
6. 下列命题中，真命题为（）

A、有理数的绝对值是正数 B、平行于同一条直线的两条直线平行 C、同旁内角互补 D、过一点有且只有一条直线与已知直线平行

查看试题解析
7. $4$ 月下旬，在石景山区 $2023$ 年“西部温暖计划”启动仪式后，某校组织师生开展捐赠活动．为了解某班 $30$ 名学生捐赠物品情况，对每位学生的捐赠数量进行了收集、整理，并绘制统计图如图所示．这组数据的中位数、众数分别为（）

A、 $9 ， 10$ B、 $8 ， 10$ C、 $4 ， 5$ D、 $4.5 ， 5$

查看试题解析
8. 已知：关于 $x$ 的不等式组 ${\begin{array}{l} x - a \geq 0 ， \\ 2 x < 4 \end{array}$ 只有三个整数解，则 $a$ 的取值范围是（）

A、 $- 2 < a \leq - 1$ B、 $- 2 \leq a \leq - 1$ C、 $- 2 \leq a < - 1$ D、 $- 2 < a < - 1$

查看试题解析

二、填空题

9. 计算： $3^{- 2} =$ ； ${(π - 2)}^{0} =$ ．

查看试题解析
10. 若 $a^{12} = {(a^{3})}^{m} = a^{2} \cdot a^{n}$ ，则 $m =$ ； $n =$ ．

查看试题解析
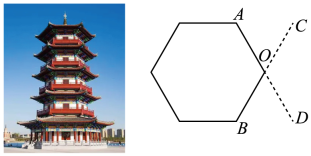
11. 若一个角是这个角的余角的 $4$ 倍，则这个角的度数为．

查看试题解析
12. 为了测量一座古塔外墙底部的底角∠AOB的度数，李潇同学设计了如下测量方案：作AO，BO的延长线OD，OC，量出∠COD的度数，从而得到∠AOB的度数．这个测量方案的依据是．

查看试题解析
13. 已知： $a > b$ ，请写出一个使不等式 $a m < b m$ 成立的m的值，这个值可以为．

查看试题解析
14. 著名数学家华罗庚曾用诗词表达了“数形结合”的思想，其中谈到“数缺形时少直观，形少数时难入微”．如图是由四个长为a，宽为b的长方形拼摆而成的正方形，其中 $a > b > 0$ ．根据图形写出一个正确的等式，可以表示为．

查看试题解析
15. 某篮球架及侧面示意图如图所示，若 $∠ E D C = 150 °$ ， $D E ∥ A B$ ， $C B ⊥ A B$ 于点B，则 $∠ G C B =$ $°$ ．

查看试题解析

三、解答题

16. 小石的妈妈需要购买盒子存放 $15$ 升的食物，且要求每个盒子要装满．现有 $A ， B$ 两种型号的盒子，单个盒子的容量和价格如下表．
型号
          $A$
          $B$
单个盒子容量（升）
          $2$
          $3$
单价（元）
          $13$
          $15$

(1)、写出一种购买方案，可以为；

(2)、恰逢五一假期， $A$ 型号盒子正在做促销活动，即购买三个及三个以上可一次性返现金 $10$ 元，则购买盒子所需要的最少费用为元．

查看试题解析
17. 因式分解：

(1)、 $3 x^{2} - 12$ ；

(2)、 $x^{2} - 2 x - 8$ ．

查看试题解析
18. 计算： $- a^{2} (- 2 a b) + 3 a (a^{2} b - 1)$

查看试题解析
19. 解方程组 ${\begin{array}{l} 2 x - y = 5 ， \\ 3 x + 2 y = - 3 . \end{array}$

查看试题解析
20. 运用乘法公式简便计算： $98 \times 102$ ．

查看试题解析
21. 计算： ${(2 x - 3)}^{2} - (x + 3) (x - 2)$ ．

查看试题解析
22. 已知： $m - n = - 2$ ， $m n = 3$ ，求代数式 $- m^{3} n + 2 m^{2} n^{2} - m n^{3}$ 的值．

查看试题解析
23. 解不等式组 ${\begin{array}{l} 5 (x - 1) \leq x + 3 ， \\ \frac{x + 1}{2} < 2 x . \end{array}$ ．

查看试题解析
24. 已知：如图，直线 $A B ， C D$ 与直线 $E F$ 分别交于点M，N， $∠ 1 + ∠ 2 = 180 °$ ， $B H$ 平分 $∠ A B D$ ，交 $C D$ 于点H．

求证： $∠ 4 = \frac{1}{2} ∠ 3$ ．
请补全下面的证明过程：
证明：∵ $∠ 1 +$        ▲   $= 180 °$ （平角的定义），
      $∠ 1 + ∠ 2 = 180 °$ （已知），
∴       ▲   $= ∠ 2$ （  ），
∴ $A B ∥ C D$ （同位角相等，两直线平行）．
∴ $∠ A B D = ∠ 3$ （  ）．
∵ $B H$ 平分 $∠ A B D$ （已知），
∴       ▲  （角平分线的定义）．
∴ $∠ 4 = \frac{1}{2} ∠ 3$ （  ）．

查看试题解析

25. 为响应习近平总书记提出的“绿水青山就是金山银山”的口号，某校在植树节到来之际，开展植树活动．学校计划购买紫薇和银杏两种树苗，相关信息如下表：

编号	名称	规格单位	单价	购买数量	预算金额（元）
$1$	紫薇	$1$ 棵	$18$	$m$ （棵）	$2400$
$2$	银杏	$1$ 捆（ $2$ 棵装）	$20$	$n$ （捆）	$2400$

(1)、若两种树苗共买

200

棵，恰好将预算金额花完，求

m ， n

的值；

(2)、高一年级共有学生

298

人，老师

22

人．若要保证师生每两人种一棵树，在预算金额不增加的情况下，最多可以购买紫薇树苗多少棵？

查看试题解析

26. 2023年5月8日是第76个世界红十字日．某校以“生命教育‘救’在身边”为主题开展“红十字博爱周”活动．为了增强学生的急救意识，宣传急救知识，对七年级200名学生开展急救知识竞赛．为了解七年级学生急救知识掌握情况，调查小组进行了抽样调查，过程如下：

(1)、收集数据调查小组计划从七年级选取20名学生的竞赛成绩（百分制）作为样本，下面的抽样方法中，合理的是____（填字母）．

A、从七年级的救护技能培训班中选取20名学生的竞赛成绩组成样本； B、从七年级选取20名女生的竞赛成绩组成样本； C、从七年级随机选取20名学生的竞赛成绩组成样本．

(2)、抽样方法确定后，调查小组抽取得到七年级的样本数据如下：

68 88 84 78 92 83 95 88 100 92

86 95 79 76 99 97 88 93 99 100

整理、描述数据按如下分数段整理、描述样本数据：

七年级样本成绩统计表

成绩x（单位：分）	划记	频数
$65 \leq x < 80$
$80 \leq x < 85$	丅	2
$85 \leq x < 90$		4
$90 \leq x < 95$
$95 \leq x \leq 100$	正丅	7

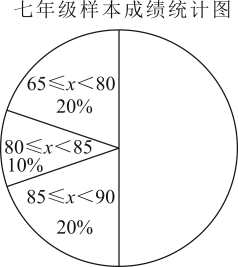
解决问题

①请将统计表、扇形统计图补充完整；

②估计该校七年级学生竞赛成绩不低于90分的学生有名．

查看试题解析

27. 如图， $A C ， B C$ 被 $A B$ 所截， $A D ⊥ B C$ 于点D．E为直线 $A B$ 上一点，过点E作 $B C$ 的垂线，垂足为F，过点D作 $D G ∥ A B$ 交 $A C$ 于点G．

(1)、若点E在线段 $A B$ 上，
①根据题意补全图形；
②判断 $∠ A E F$ 与 $∠ A D G$ 的数量关系，并证明；

(2)、若点E不在线段 $A B$ 上，直接写出 $∠ A E F$ 与 $∠ A D G$ 的数量关系为；

(3)、通过本题前两问的解决，观察 $∠ A E F$ 与 $∠ A D G$ 的位置关系和数量关系，归纳出一个你发现的结论．

查看试题解析
28. 对于二元一次方程 $x - 2 y = 2$ 的任意一个解 ${\begin{array}{l} x = m ， \\ y = n ， \end{array}$ 给出如下定义：若 $| m | \geq | n |$ ，则称 $| m |$ 为方程 $x - 2 y = 2$ 的“关联值”；若 $| m | < | n |$ ，则称 $| n |$ 为方程 $x - 2 y = 2$ 的“关联值”．

(1)、写出方程 $x - 2 y = 2$ 的一个解，并指明此时方程的“关联值”；

(2)、若“关联值”为4，写出所有满足条件的方程的解；

(3)、直接写出方程 $x - 2 y = 2$ 的最小“关联值”为；当关联值为 $| m |$ 时，直接写出x的取值范围是．

查看试题解析

型号	$A$	$B$
单个盒子容量（升）	$2$	$3$
单价（元）	$13$	$15$