北京市密云区2022—2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 9的平方根是( )A、 B、3 C、 D、2. 下列利用三角板过点P画直线的垂线 , 正确的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列数轴上,正确表示不等式的解集的是( )A、
3. 下列数轴上,正确表示不等式的解集的是( )A、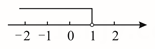 B、
B、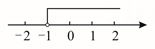 C、
C、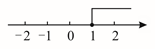 D、
D、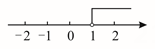 4. 如图,三角形的边在直线上,且 . 将三角形沿直线向右平移得到三角形 , 其中点的对应点为点 . 若平移的距离为 , 则的长为( )
4. 如图,三角形的边在直线上,且 . 将三角形沿直线向右平移得到三角形 , 其中点的对应点为点 . 若平移的距离为 , 则的长为( ) A、 B、 C、 D、5. 在平面直角坐标系中,点位于第三象限,则( )A、 B、 C、 D、6. 下列每对数值中是方程x-3y=1的解的是( )A、 B、 C、 D、7. 某电商网站以智能手表为主要的产品运营.今年1—4月份,该网站智能手表的销售总额如图1所示,其中一款通话功能智能手表的销售额占当月智能手表销售总额的百分比如图2所示.
A、 B、 C、 D、5. 在平面直角坐标系中,点位于第三象限,则( )A、 B、 C、 D、6. 下列每对数值中是方程x-3y=1的解的是( )A、 B、 C、 D、7. 某电商网站以智能手表为主要的产品运营.今年1—4月份,该网站智能手表的销售总额如图1所示,其中一款通话功能智能手表的销售额占当月智能手表销售总额的百分比如图2所示.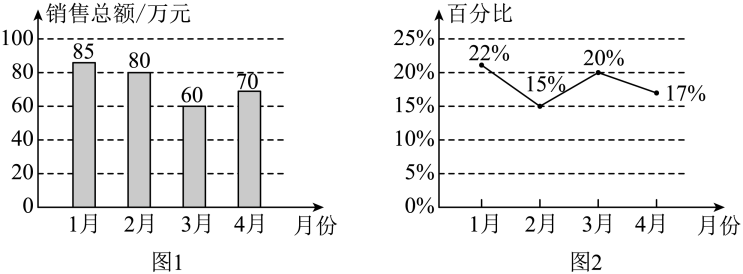
以下四个结论正确的是( )
A、今年1—4月,智能手表的销售总额连续下降 B、今年1—4月,通话功能智能手表的销售额在当月智能手表销售总额中的占比连续下降 C、通话功能智能手表3月份的销售额与2月份的销售额持平 D、今年1—4月,通话功能智能手表销售额最低的月份是2月8. 在平面直角坐标系中,点、、 , 其中点在点左侧.连接 , , 若在、、所围成的区域内(含边界),横坐标和纵坐标都为整数的点的个数为6,则的取值范围是( )A、 B、 C、 D、二、填空题
-
9. 实数的相反数是 .10. 用不等式表示“的3倍与20的和小于或等于7”为 .11. 若是方程的解,则a的值为 .12. 若 , 且 , 是两个连续的整数,则的值为 .13. 学习了平行线后,小强同学想出了“过直线外一点画一条已知直线的平行线”的新方法,他的作图步骤如下:

老师说小强的作图方法是正确的,其中能够说明两条直线平行的依据是 .
14. 用一组a,b的值说明命题“若a2>b2 , 则a>b”是错误的,这组值可以是a= , b= .15. 《算法统宗》是中国古代数学名著,作者是明代著名数学家程大位.在其中有这样的记载“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”译文:有100名和尚分100个馒头,正好分完.如果大和尚一人分3个,小和尚3人分一个,试问大、小和尚各有几人?设有大和尚x人,小和尚y人,可列方程组为 . 16. 平面上两条直线 , 相交于点 . 对于平面上任意一点 , 若点到直线的距离为 , 到直线的距离为 , 则称有序数对为点的“距离坐标”.如图所示,点的“距离坐标”为(3,2).
16. 平面上两条直线 , 相交于点 . 对于平面上任意一点 , 若点到直线的距离为 , 到直线的距离为 , 则称有序数对为点的“距离坐标”.如图所示,点的“距离坐标”为(3,2).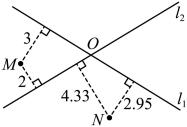 (1)、结合图形,直接写出点的“距离坐标”为;(2)、在该平面内,“距离坐标”为(5,5)的点共有个.
(1)、结合图形,直接写出点的“距离坐标”为;(2)、在该平面内,“距离坐标”为(5,5)的点共有个.三、解答题
-
17. 计算:18. 计算:19. 解方程组20. 解不等式组 , 并写出它的负整数解.21. 完成下列计算,并在括号内填写推理依据.
如图, , 直线分别交、于点E和点F,过点E作交直线于点G.若 , 计算的度数.

解:∵ ,
∴ ▲ ( ).
∵ ,
∴ ( ).
∴ ▲ .
22. 北京环球影城主题公园完美融合中外经典文化元素,打造了变形金刚基地、未来水世界等七大主题景区.下图是某些主题景区的分布示意图(图中小方格都是边长为1个单位长度的正方形).小珂和妈妈在游玩的过程中,分别对“侏罗纪世界”和“变形金刚基地”的位置做出如下描述:小珂:“侏罗纪世界的坐标是”.
妈妈:“变形金刚基地位于坐标原点的西北方向”.
实际上,小珂和妈妈描述的位置都是正确的.
 (1)、根据以上描述,在图中建立平面直角坐标系,并写出“未来水世界”的坐标:;(2)、若“哈利波特魔法世界”的坐标为 , “好莱坞”的坐标为 , 请在坐标系中用点M、N表示这两个主题景区的位置;(3)、如果一个单位长度代表35米,请你从方向和距离的角度描述“好莱坞”相对于“变形金刚基地”的大致位置.23. 某公益团体组织“义卖助学,奉献爱心”活动,计划购进红、白两种颜色的文化衫通过手绘设计后进行出售,并将所获利润全部捐资助学.已知该公益团体花费了2400元从批发商城购买了红、白两种颜色的文化衫100件,每件文化衫的批发价格及手绘后的零售价格如下表所示:
(1)、根据以上描述,在图中建立平面直角坐标系,并写出“未来水世界”的坐标:;(2)、若“哈利波特魔法世界”的坐标为 , “好莱坞”的坐标为 , 请在坐标系中用点M、N表示这两个主题景区的位置;(3)、如果一个单位长度代表35米,请你从方向和距离的角度描述“好莱坞”相对于“变形金刚基地”的大致位置.23. 某公益团体组织“义卖助学,奉献爱心”活动,计划购进红、白两种颜色的文化衫通过手绘设计后进行出售,并将所获利润全部捐资助学.已知该公益团体花费了2400元从批发商城购买了红、白两种颜色的文化衫100件,每件文化衫的批发价格及手绘后的零售价格如下表所示:类别
每件批发价格(元)
手绘零售价格(元)
红色文化衫
25
45
白色文化衫
20
35
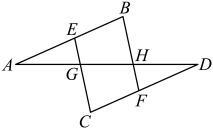
(1)、该公益团体购进红、白文化衫各多少件?(2)、这批文化衫通过手绘设计后全部售出,求该公益团体“义卖助学”活动所获的利润.24. 如图,点B、C在线段异侧,E、F分别是线段、上的点,和分别交于点G和点H.已知 , , .求证: .
 25. 科技改变世界,人工智能的蓬勃发展促使人们的生活进入了智能化时代.某部门为新的生产线研发了一款机器人,为了了解它的操作技能情况,该部门选择同一个生产动作对这款机器人的操作情况进行了测试,并将收集到的数据(测试结果)进行整理、描述和分析.下面给出了部分信息.
25. 科技改变世界,人工智能的蓬勃发展促使人们的生活进入了智能化时代.某部门为新的生产线研发了一款机器人,为了了解它的操作技能情况,该部门选择同一个生产动作对这款机器人的操作情况进行了测试,并将收集到的数据(测试结果)进行整理、描述和分析.下面给出了部分信息.a.机器人20次测试成绩(十分制)的频数分布表如下:
成绩段(单位:分)
频数
频率
3
0.15
0.40
4
0.20
合计
20
1.00
b.机器人20次测试成绩的频数分布直方图和扇形图如下:

(说明:成绩在9.0分及以上为操作技能优秀,8.0~8.9分为操作技能良好,6.0~7.9分为操作技能合格,6.0分以下为操作技能不合格)
根据以上信息,回答下列问题:
(1)、表中的值为 , 的值为 , 的值为;(2)、补全频数分布直方图;(3)、扇形统计图中“成绩段”所对应的扇形的圆心角度数是;(4)、如果生产出一个产品,需要完成同样的操作200次,请你估计机器人生产这个产品达到操作技能优秀的次数.26. 阅读材料,解决问题:解答“已知 , 且 , , 试确定的取值范围”有如下解法:
解: ∵ ,
∴ .
∵ ,
∴ .
∴ .
又∵ ,
∴
同理得:
由①+②得: .
∴的取值范围是 .
请按照上述方法,完成下列问题:
(1)、已知 , 且 , , 求的取值范围;(2)、已知 , , 若成立,求的取值范围(用含m的式子表示).27. 已知:如图,直线 , 点A、B在直线a上(点A在点B左侧),点C、D在直线b上(点C在点D左侧),和相交于点E.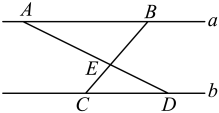 (1)、求证:;(2)、分别作和的角平分线相交于点F.
(1)、求证:;(2)、分别作和的角平分线相交于点F.① 结合题意,补全图形;
② 用等式表示和的数量关系,并证明.
28. 在平面直角坐标系中,对于 , 两点,给出如下定义:若 , 则称P,Q两点互为“阶依附点”.例如,点 , 点即互为“阶依附点”. (1)、已知点A的坐标为 .
(1)、已知点A的坐标为 .①在 , , 三个点中,与点A互为“阶依附点”的是;
②若点B在y轴上,且点B与点A互为“阶依附点”,直接写出点B的坐标.
(2)、已知点 , 点D与点C互为“阶依附点”,若三角形的面积为 , 求点D的坐标.