北京市延庆区2022—2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 蜜蜂建造的蜂巢既坚固又省材料，其蜂巢壁厚度约为 $0.000073$ 米，将 $0.000073$ 用科学记数法表示为（）

A、 $7.3 \times 1 0^{- 4}$ B、 $7.3 \times 1 0^{- 5}$ C、 $73 \times 1 0^{- 7}$ D、 $7.3 \times 1 0^{6}$

查看试题解析
2. 下列运算正确的是（）

A、 $a^{3} + a^{2} = a^{5}$ B、 $a^{6} \div a^{3} = a^{2}$ C、 ${(- 2 a^{2})}^{3} = 6 a^{6}$ D、 $a^{3} \cdot a = a^{4}$

查看试题解析
3. 若 $a > b$ ，则下列各式不正确的是（）

A、 $a + 2 > b + 2$ B、 $a - 2 > b - 2$ C、 $- 2 a > - 2 b$ D、 $\frac{a}{2} > \frac{b}{2}$

查看试题解析
4. 如图，直线 $a$ ， $b$ 相交于点O，如果 $∠ 1 + ∠ 2 = 120 °$ ，那么 $∠ 3$ 的度数为（）

A、150° B、120° C、60° D、30°

查看试题解析
5. 如图，点 $O$ 在直线 $A B$ 上， $O C ⊥ O D$ ．若 $∠ A O C = 120 °$ ，则 $∠ B O D$ 的大小为（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
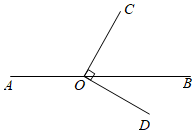6. 如果 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是关于x，y的二元一次方程 $3 x + m y = 5$ 的一个解，那么m的值为（）

A、 $- 1$ B、5 C、2 D、1

查看试题解析
7. 下列采用的调查方式中，合适的是（）

A、为了解妫水河的水质情况，采用抽样调查方式 B、某工厂为了解所生产的产品的合格率，采用全面调查的方式 C、某学校给学生做校服前进行尺寸大小的调查，采用抽样调查的方式 D、为了解神舟飞船设备零件的质量情况，采用抽样调查的方式

查看试题解析
8. 如图，下列条件中能判断 $B C ∥ E F$ 的是（）
① $∠ 1 = ∠ E$ ；② $∠ 2 = ∠ E$ ；③ $∠ B = ∠ 1$ ；④ $∠ E + ∠ E G C = 180 °$ ．

A、①②③④ B、①②③ C、①③④ D、①②④

查看试题解析

二、填空题

9. 计算： ${(\frac{1}{3})}^{- 1} + {(π - 1)}^{0} =$ ．

查看试题解析
10. 计算： $36 a^{3} b^{4} \div 9 a^{2} b$ = ．

查看试题解析
11. 已知 $∠ A = 65 °$ ，如果 $∠ B$ 是 $∠ A$ 的余角，那么 $∠ B =$ ．

查看试题解析
12. 如图，直线l₁ ， l₂ ， l₃交于一点，直线l₄∥l₁ ，若∠1＝124°，∠2＝88°，则∠3的度数为．

查看试题解析
13. 有A，B两组数据，如下表所示：

A

11

12

13

14

15

B

12

12

13

14

14

A，B两组数据的平均数分别为 ${\bar{x}}_{1}$ ， ${\bar{x}}_{2}$ ，则 ${\bar{x}}_{1}$ ${\bar{x}}_{2}$ ．（填“＞”“＜”或“＝”）

查看试题解析
14. 为了说明“如果 $a > b$ ，那么 $a^{2} > b^{2}$ ”是假命题，则a，b可以取的一组值是 $a =$ ， $b =$ ．

查看试题解析
15. 《九章算术》是中国传统数学的重要著作，方程术是它的最高成就.其中记载：今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？译文：今有人合伙购物，每人出8钱，会多3钱；每人出7钱，又会差4钱，问人数、物价各是多少？设合伙人数为x人，物价为y钱，根据题意可列出方程组.

查看试题解析
16. 观察一组按规律排列的代数式： $a + 2 b ， a^{2} - 2 b^{3} ， a^{3} + 2 b {}_{5}， a^{4} - 2 b^{7} ， \cdot \cdot \cdot ，$ 第 $n$ 个式子是．（ $n$ 为正整数）

查看试题解析

三、解答题

17. 分解因式：

(1)、 $a^{3} - 4 a$ ；

(2)、 $x^{3} - 10 x^{2} + 25 x$ ．

查看试题解析
18. 计算： $(a + 2) (a - 2) - a (a + 3)$ ．

查看试题解析
19. 解方程组：

(1)、 ${\begin{array}{l} x + y = 5 \\ 2 x - y = 1 \end{array}$ ；

(2)、 ${\begin{array}{l} 3 x + y = 6 \\ x + 2 y = 7 \end{array}$ ．

查看试题解析
20. 解不等式： $2 (x - 4) > 2 - 3 x$ ，并把它的解集在数轴上表示出来．

查看试题解析
21. 解不等式组 ${\begin{array}{l} 3 (x + 1) > x - 1 \\ \frac{x + 9}{2} > 2 x \end{array}$ 并写出所有的整数解．

查看试题解析
22. 先化简，再求值： $(x + 1)^{2} + (x + 1) (2 x - 1)$ ，其中 $x = - 2$ ．

查看试题解析

四、填空题

23. 已知：如图，点 $E$ 为线段 $D F$ 上的点，点 $B$ 为线段 $A C$ 上的点，连接 $D B$ ， $E C$ ， $A F$ ， $∠ 1 = ∠ 2$ ， $∠ C = ∠ D$ ，求证： $∠ F = ∠ A$ ．

证明：∵ $∠ 1 = ∠ 2$ （已知），
∴ $D B ∥$        ▲       （  ），
∴ $∠ C = ∠ A B D$ （  ），
∵ $∠ C = ∠ D$ （已知），
∴ $∠ A B D =$        ▲  ，
∴ $D F ∥ A C$ ，
∴ $∠ F = ∠ A$ （  ）．

查看试题解析

五、解答题

24. 已知：如图， $A B ∥ C D$ ，直线 $A E$ 交 $C D$ 于点C， $∠ A = 125 ° ， ∠ D = 55 °$ ，求证： $A E ∥ D F$ ．

查看试题解析
25. 为丰富学生课余生活，某中学体育组计划从同一个体育用品店一次性购买一些篮球和足球 $.$ 已知 $1$ 个篮球和 $3$ 个足球共需要2 $90$ 元； $2$ 个篮球和 $1$ 个足球共需要 $230$ 元．

(1)、求每个篮球和每个足球各多少元；

(2)、该体育组根据实际需要，准备购买篮球和足球共 $6$ 个，且篮球个数不少于 $2$ 个，总费用不超过 $450$ 元，有哪几种购买方案？

查看试题解析
26. 为了解学生的阅读情况，小华设计调查问卷，用随机抽样的方式调查了部分学生，并对相关数据进行了收集、整理、描述和分析.下面是其中的部分信息：
a.将学生每天阅读时长数据分组整理，绘制了如下两幅不完整的统计图表
七年级学生每天阅读时长情况统计表

组别
平均每天阅读时长
（单位：分钟）
人数
（单位：人）
A
          $0 \leq x < 30$
8
B
          $30 \leq x < 60$
n
C
          $60 \leq x < 90$
16
D
          $90 \leq x < 120$
8
七年级学生每天阅读时长情况扇形统计图

b.平均每天阅读时长在 $60 \leq x < 90$ 的具体数据如下：
60  60  66  68  69  69  70  70  72  73  73  73  80  83  84  85
根据以上信息，回答下列问题：

(1)、表中 $n =$ ，图中 $m =$ ；

(2)、A组这部分扇形的圆心角是°；

(3)、平均每天阅读时长在 $60 \leq x < 90$ 这组具体数据的中位数是，众数是；

(4)、若该校七年级共有学生500人，根据调查结果估计平均每天阅读时长少于半小时的学生约有人．

查看试题解析
27. 已知：如图，点D在线段 $A B$ 上，过点D作 $D E ∥ B C$ 交线段 $A C$ 于点E，连接 $C D$ ，过点D作 $D F ⊥ B C$ 于点F，过点F作 $F G ∥ C D$ 交线段 $A B$ 于点G．

(1)、依题意补全图形；

(2)、用等式表示 $∠ C D E$ 与 $∠ D F G$ 的数量关系，并证明．

查看试题解析
28. 给出如下定义：如果一个未知数的值使得方程和不等式（组）同时成立，那么这个未知数的值称为该方程与不等式（组）的“关联解”．
例如：已知方程 $3 x - 2 = 1$ 和不等式 $x + 4 > 0$ ，对于未知数 $x$ ，当 $x = 1$ 时，使得 $3 \times 1 - 2 = 1$ ， $x + 4 = 1 + 4 = 5 > 0$ 同时成立，则称 $x = 1$ 是方程 $3 x - 2 = 1$ 与不等式 $x + 4 > 0$ 的“关联解”．

(1)、判断 $x = 3$ 是否是方程 $2 x - 6 = 0$ 与不等式 $2 (x + 3) < 4$ 的“关联解”（填是或否）；
判断 $x = - 1$ 是方程 $2 x + 3 = 1$ 与不等式（组）① $x - \frac{1}{2} < \frac{3}{2}$ ， ② $\frac{x - 1}{2} > 3$ ， ③ ${\begin{array}{l} x - 2 > 0 \\ x - 5 < 0 \end{array}$ 中的“关联解”；（只填序号）

(2)、如果 $x = 2$ 是关于 $x$ 的方程 $2 x - a = 0$ 与关于 $x$ 的不等式组 ${\begin{array}{l} \frac{x + 1}{2} > - 1 \\ 1 + 2 (x - a) \leq b \end{array}$ 的“关联解”，那么 $a =$ ， $b$ 的取值范围是；

(3)、如果 $x = m$ 是关于 $x$ 的方程 $x - 2 n = 4$ 与关于 $x$ 的不等式组 ${\begin{array}{l} n - m + x > - \frac{1}{2} \\ m - n - x > - 1 \end{array}$ 的“关联解”，求 $m$ 的取值范围．

查看试题解析

组别	平均每天阅读时长（单位：分钟）	人数（单位：人）
A	$0 \leq x < 30$	8
B	$30 \leq x < 60$	n
C	$60 \leq x < 90$	16
D	$90 \leq x < 120$	8