北京市怀柔区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 有理数9的算术平方根是( )A、 B、 C、3 D、2. 通过平移,可将图中的北京冬奥会吉祥物“雪容融”移动到图( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列各组数值中,哪个是方程的解( )A、 B、 C、 D、4. 若点在平面直角坐标系中的第二象限,则x的值可能是( )A、0 B、2 C、4 D、5. 设x,y是实数,若 , 则下列式子正确的是( )A、 B、 C、 D、6. 如图,下列判断正确的是( )
3. 下列各组数值中,哪个是方程的解( )A、 B、 C、 D、4. 若点在平面直角坐标系中的第二象限,则x的值可能是( )A、0 B、2 C、4 D、5. 设x,y是实数,若 , 则下列式子正确的是( )A、 B、 C、 D、6. 如图,下列判断正确的是( )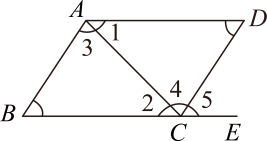 A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 估计的值在哪两个数之间( )A、与 B、与 C、与 D、与8. 某校九年级两个班的师生一起到某区教育基地进行社会大课堂活动,该基地成人门票120元/人,学生门票98元/人,已知该校此次活动共支付6720元,且该校学生人数比教师人数9倍少3人,请问该校教师和学生各有几人?若设教师有x人,学生有y人,则根据题意列方程组正确的是( )A、 B、 C、 D、9. 已知a是负数,下列关于x的不等式组无解的是( )A、 B、 C、 D、10. 某学校准备为七年级学生开设共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 估计的值在哪两个数之间( )A、与 B、与 C、与 D、与8. 某校九年级两个班的师生一起到某区教育基地进行社会大课堂活动,该基地成人门票120元/人,学生门票98元/人,已知该校此次活动共支付6720元,且该校学生人数比教师人数9倍少3人,请问该校教师和学生各有几人?若设教师有x人,学生有y人,则根据题意列方程组正确的是( )A、 B、 C、 D、9. 已知a是负数,下列关于x的不等式组无解的是( )A、 B、 C、 D、10. 某学校准备为七年级学生开设共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).选修课
人数
40
60
100
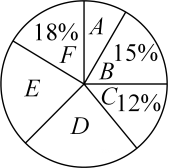
下列说法不正确的是( )A、这次被调查的学生人数为400人 B、对应扇形的圆心角为 C、喜欢选修课的人数为72人 D、喜欢选修课的人数最少二、填空题
-
11. 计算: = .12. 调查某区小学、初中、高中所有学生的手机使用时长,这种调查适合用(填“普查”或“抽样调查”).13. 若是方程的一个解,则a的值是 .14. 若点在x轴上,则点A坐标为 .15. 若关于x的一元一次方程的解是负数,则m的取值范围是 .16. 如图所示,一副三角板摆放在桌面上,其中边在同一条直线上,则 , 依据是 .
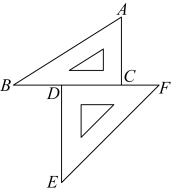 17. 假设m,n都是无理数,且满足 . 请写出满足以上条件的一组值 , .18. 某贸易公司有120吨商品需要运出,现有甲、乙、丙三种车型供运输选择.每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
17. 假设m,n都是无理数,且满足 . 请写出满足以上条件的一组值 , .18. 某贸易公司有120吨商品需要运出,现有甲、乙、丙三种车型供运输选择.每辆车的运载能力和运费如下表所示:(假设每辆车均满载)车型
甲
乙
丙
运载量(吨/辆)
5
8
10
运费(元/辆)
450
600
700
(1)、全部商品一次性运送可用甲型车8辆.乙型车5辆,丙型车辆.(2)、若该公司打算用甲、乙、丙三种车型同时参与运送,已知车辆总数为14辆,且一次性运完所有商品,此时的总运费为元.三、解答题
-
19. 解方程组:(1)、(2)、20. 解不等式 , 并把它的解集在数轴上表示出来.
 21. 解不等式组并求出它的非负整数解.22. 如图,在射线上有一点 , 请选择适当的工具作图,完成以下问题:
21. 解不等式组并求出它的非负整数解.22. 如图,在射线上有一点 , 请选择适当的工具作图,完成以下问题: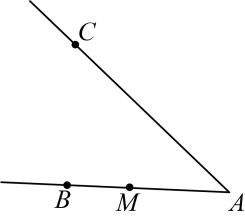 (1)、过点作射线的垂线,垂足为点;(2)、在线段上任取一点(不与 , 重合),连接;(3)、在线段 , , 中,线段最短,依据是 .23. 如图,已知 , , 于点C, , 求的度数.
(1)、过点作射线的垂线,垂足为点;(2)、在线段上任取一点(不与 , 重合),连接;(3)、在线段 , , 中,线段最短,依据是 .23. 如图,已知 , , 于点C, , 求的度数.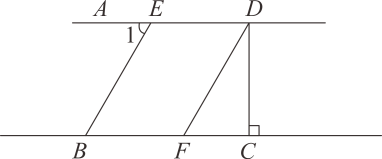 24. 小明家住在湖光小区,下图是小明家附近地方的平面示意图,图中小方格都是边长为1个单位长度的正方形,其中第一中学的坐标为 , 康德乐的坐标为 .
24. 小明家住在湖光小区,下图是小明家附近地方的平面示意图,图中小方格都是边长为1个单位长度的正方形,其中第一中学的坐标为 , 康德乐的坐标为 .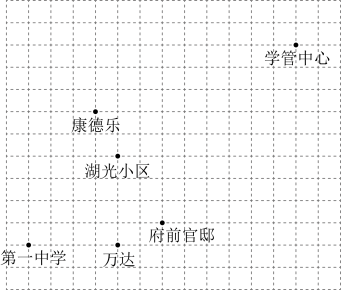 (1)、请在图中画出平面直角坐标系,并写出学管中心的坐标:(2)、若大世界的坐标为 , 请在坐标系中用点P表示它的位置;(3)、小明家从湖光小区搬家到府前官邸 , 请你用坐标描述平移的过程.25. 某学校开展居家体育训练,倡导学生在家开展体育锻炼.返校后,校学生会随机抽取了部分学生,就“平均每天开展体育锻炼所用时长”进行了调查,以下是根据相关数据绘制的统计图的一部分:
(1)、请在图中画出平面直角坐标系,并写出学管中心的坐标:(2)、若大世界的坐标为 , 请在坐标系中用点P表示它的位置;(3)、小明家从湖光小区搬家到府前官邸 , 请你用坐标描述平移的过程.25. 某学校开展居家体育训练,倡导学生在家开展体育锻炼.返校后,校学生会随机抽取了部分学生,就“平均每天开展体育锻炼所用时长”进行了调查,以下是根据相关数据绘制的统计图的一部分: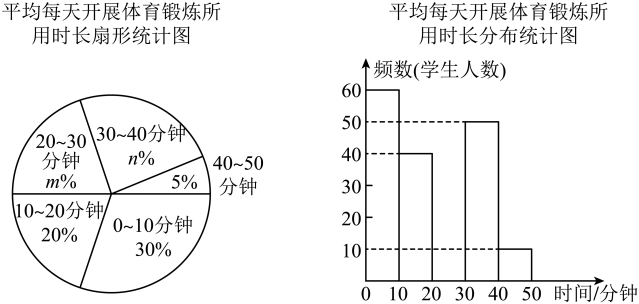
根据上述信息,回答下列问题:
(1)、在本次随机抽取的样本中,调查的样本容量为;(2)、m= , n=;(3)、补全频数分布直方图;(4)、如果该校共有学生2000人,请你估计“平均每天开展体育锻炼的时长不少于30分钟”的学生大约有多少人?26. 列二元一次方程组解应用题.某校初一年级举行“书香润心灵,阅读促成长”活动.学校要求各班班长根据学生阅读需求统计将要购买的书类型和书籍数量,下表是初一(1)班和初一(2)班统计后的购书情况.
文学类(本/人)
科普类(本/人)
初一(1)
3
2
初一(2)
4
1
共计(本)
258
102
(1)、请你根据表格信息,求初一(1)班和初一(2)班各有多少人?(2)、若学校准备为初一(1)班和初一(2)班购买文学类书籍和科将类书籍共300本,且文学类书籍不少于科普类书籍的2倍,请问最多能购买多少本科普类书籍?27. 如图,直线与的两边交于 , 两点, , 点是边上一个动点,连接 .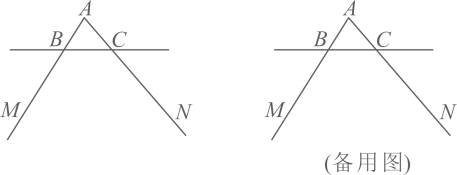 (1)、过点作 , 交射线于点 , 依题意补全图形,
(1)、过点作 , 交射线于点 , 依题意补全图形,①直接写出的度数(用含α的式子表示);
②若点 , 在 , 的延长线上,并且直线 , 当平分时,求的度数(用含的式子表示);小林在思考这道题时,想到过点作交射线于点 , 通过转化角可以求出的度数.你可以利用小林的思路解答此题也可以独立思考求出的度数.
(2)、参考小林思考问题的方法,解决问题:若点 , 在 , 的延长线上,并且直线 , 当点在上运动时,直接用含的等式表示 , , 的数量关系.28. 在平面直角坐标系中,点 , 过点P作轴,垂足为点H,给出如下定义:将点H向右平移个单位,得到点Q,则称点Q是点P关于x轴的折对点;当时,则称d为点P关于点Q的折对距离. (1)、点关于x轴的折对点的坐标是 , 折对距离为;(2)、点Q是点P关于x轴的折对点,若折对点 , 写出一个符合条件的P点坐标;(3)、已知点 , , 以线段AB为边,在x轴上方作正方形 , 在正方形上存在点P,且点P关于点Q的折对距离 , 直接写出t的取值范围.
(1)、点关于x轴的折对点的坐标是 , 折对距离为;(2)、点Q是点P关于x轴的折对点,若折对点 , 写出一个符合条件的P点坐标;(3)、已知点 , , 以线段AB为边,在x轴上方作正方形 , 在正方形上存在点P,且点P关于点Q的折对距离 , 直接写出t的取值范围.