北京市燕山地区2022—2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. $π$ 的相反数是（）

A、 $π$ B、 $- π$ C、 $\pm π$ D、 $\frac{1}{π}$

查看试题解析
2. 在下面的四个图案中，可以通过平移图案得到的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，点 $O$ 在直线 $A B$ 上， $O C ⊥ O D$ ，若 $∠ B O D = 40 °$ ，则 $∠ A O C$ 的度数是（）

A、 $120 °$ B、 $130 °$ C、 $140 °$ D、 $150 °$

查看试题解析
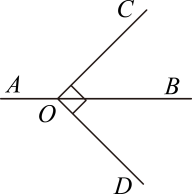4. 党的二十大报告提出“深化全民阅读活动”．某校开展了“书香浸润心灵阅读点亮人生”读书系列活动．为了解学生的课外阅读情况，从全校2000名学生记录的一周的课外阅读时间（单位：小时）中随机抽取了200名学生课外阅读时间（单位：小时）进行统计，在这个问题中以下说法正确的是（）

A、200名学生一周的课外阅读时间是样本 B、200名学生是总体 C、此调查为全面调查 D、样本容量是2000

查看试题解析
5. 在数轴上表示不等式 $2 x - 6 < 0$ 的解集，正确的是（）

A、 B、 C、 D、

查看试题解析
6. 两位同学在讨论一个一元一次不等式．
强强说：“不等式在求解的过程中需要改变不等号的方向．”
国国说：“不等式的解集为 $x \leq 5$ ． ”
根据上面对话提供的信息，他们讨论的不等式是（）

A、 $- 2 x \geq - 10$ B、 $2 x < 10$ C、 $- 2 x > 10$ D、 $- 2 x \leq - 10$

查看试题解析
7. a，b在数轴上的对应点的位置如图所示，则正确的结论是（）

A、 $a > - 2$ B、 $| a | < | b |$ C、 $a b > 0$ D、 $a < - b$

查看试题解析
8. 我国古代数学经典著作《九章算术》中有这样一题，原文是：“今有共买物，人出八，盈三；人出七，不足四．问人数、物价各几何？”意思是：今有人合伙购物，每人出八钱，会多三钱；每人出七钱，又差四钱．问人数、物价各多少？设人数为 $x$ 人，物价为 $y$ 钱，下列方程组正确的是（）

A、 ${\begin{array}{l} 8 x - y = 3 \\ 7 x - y = - 4 \end{array}$ B、 ${\begin{array}{l} 8 x + y = 3 \\ 7 x - y = - 4 \end{array}$ C、 ${\begin{array}{l} 8 x - y = 3 \\ 7 x - y = 4 \end{array}$ D、 ${\begin{array}{l} 8 x - y = - 3 \\ 7 x + y = - 4 \end{array}$

查看试题解析

9. 小明用计算器求了一些正数的平方，记录如下表．

x	15	15.1	15.2	15.3	15.4	15.5	15.6	15.7	15.8	15.9	16
$x^{2}$	225	228.01	231.04	234.09	237.16	240.25	243.36	246.49	249.64	252.81	256

下面有四个推断：

① $\sqrt{2.2801}$ ＝1.51

②一定有3个整数的算术平方根在15.5～15.6之间

③对于小于15的两个正数，若它们的差等于0.1，则它们的平方的差小于3.01

④16.2²比16.1²大3.23

所有合理推断的序号是（　　）

A、①② B、③④ C、①②④ D、①②③④

查看试题解析

10. 如图，在平面直角坐标系中，一动点从原点 $O$ 出发，按向上，向右，向下，向右的方向不断地移动，每移动一个单位，得到点 $A_{1} (0 ， 1)$ ， $A_{2} (1 ， 1)$ ， $A_{3} (1 ， 0)$ ， $A_{4} (2 ， 0)$ ， …那么点 $A_{2023}$ 的坐标为（）

A、 $A_{2023} (1011 ， 1)$ B、 $A_{2023} (1 ， 1011)$ C、 $A_{2023} (1011 ， 0)$ D、 $A_{2023} (0 ， 1011)$

查看试题解析

二、填空题

11. $\frac{49}{64}$ 的平方根是．

查看试题解析
12. 如图，一条公路两次转弯后，和原来的方向相同.如果第一次的拐角∠A是135°，则第二次的拐角∠B是，根据是.

查看试题解析
13. 下列命题中，①对顶角相等；②内错角相等；③平行于同一条直线的两条直线平行；④若 $a^{2} > b^{2}$ ，则 $a > b$ .是真命题的是．

查看试题解析
14. 用不等式表示“ $a$ 的2倍与 $b$ 的差不小于5”：．

查看试题解析
15. 若点 $P (- 3 ， 2 x)$ 位于第二象限，则 $x$ 的取值范围是．

查看试题解析
16. 已知二元一次方程组 ${\begin{array}{l} x + 3 y = 5 \\ 3 x + y = - 1 \end{array}$ ，则 $x + y =$ ， $x - y =$ ．

查看试题解析
17. 如图，点 $C$ 在射线 $B D$ 上，请你添加一个条件，使得 $A B ∥ C E$ ．

查看试题解析
18. 在平面直角坐标系中，点 $P$ 是第二象限内的点，它到 $x$ 轴和 $y$ 轴的距离相等，请写出一个满足条件的点 $P$ 的坐标．

查看试题解析
19. 小华同学统计了他所在小区居民每天手机阅读的时间，并绘制了直方图，如图所示．①小华同学一共统计了74人；②每天手机阅读不足20分钟的人数有8人；④每天手机阅读30～40分钟的人数最多；④每天手机阅读0～10分钟的人数最少．

根据图中信息，上述说法中正确的是．

查看试题解析
20. 某化工厂与 $A$ ， $B$ 两地有公路、铁路相连．这家工厂从 $A$ 地购买一批每吨1000元的原料运回工厂，制成每吨8000元的产品运到 $B$ 地．已知公路运价为1.5元 $/ (t \cdot k m)$ ，铁路运价为1.2元 $/ (t \cdot k m)$ ，且这两次运输共支出公路运费15000元，铁路运费97200元．设购买 $x t$ 原料，制成 $y t$ 产品．则从A地到这家化工厂原料运输费是，这批产品的销售款比原料费与运输费的和多元．

查看试题解析

三、解答题

21. 计算： $\sqrt{49} + \sqrt[3]{- 27} + | 1 - \sqrt{2} | - \sqrt{2}$ ．

查看试题解析
22. 解不等式组 ${\begin{array}{l} 2 x + 3 \geq x + 1 \\ \frac{2 x + 5}{3} - 1 ＜ 2 - x \end{array}$ ，并把不等式组的解集在数轴上表示出来．

查看试题解析
23. 解二元一次方程组 ${\begin{matrix} 5 x + y = - 3 ， \\ 3 x + 2 y = 1. \end{matrix}$

查看试题解析
24. 如图，直线AB与CD相交，∠1＝30°，求∠2，∠3，∠4的度数．

查看试题解析
25. 下图是北京市三所大学位置的平面示意图，图中小方格都是边长为1个单位长度的正方形，若清华大学的坐标为（0，3），北京大学的坐标为（﹣3，2）．

(1)、请在图中画出平面直角坐标系，并写出北京语言大学的坐标；

(2)、若中国人民大学的坐标为（﹣3，﹣4），请在坐标系中标出中国人民大学的位置．

查看试题解析
26. 按要求完成下列证明：
已知：如图， $A B ∥ C D$ ，直线 $A E$ 交 $C D$ 于点C， $∠ B A C + ∠ C D F = 180 °$
求证： $A E ∥ D F$
证明：∵ $A B ∥ C D$ （  ），
∴ $∠ B A C = ∠ D C E$ （  ），
∵ $∠ B A C + ∠ C D F = 180 °$ （已知），
∴       ▲   $+ ∠ C D F = 180 °$ （  ），
∴ $A E ∥ D F$ （  ），

查看试题解析
27. 开展回收废旧电池这项活动，不仅可以提高人们的环保意识，有利于倡导低碳生活方式同时，还可以为节约能源资源，保护生态环境，多做贡献．某校环保小组成员收集废旧电池．第一天收集5节1号电池，6节5号电池，总重量 $650 g$ ；第二天收集3节1号电池，4节5号电池，总重量为 $400 g$ .1节1号电池和1节5号电池的重量分别是多少？

查看试题解析

28. 华罗庚先生是中国著名数学家．为激励中国数学家在发展中国数学事业中做出突出贡献设立了“华罗庚数学奖”．小聪对截止到2023年第十六届“华罗庚数学奖”得主获奖时的年龄（单位：岁）进行收集、整理，绘制成如下的频数分布表，频数分布直方图和扇形统计图．

年龄分组	$55 \leq x < 60$	$60 \leq x < 65$	$65 \leq x < 70$	$70 \leq x < 75$	$75 \leq x < 80$	$80 \leq x < 85$	$85 \leq x < 90$
频数	3	1	11	7	$m$	3	2

根据以上信息，回答下列问题

(1)、写出

m

的值是，截止到第十六届共有人获得“华罗庚数学奖”；

(2)、补全“华罗庚数学奖”得主获奖年龄频数分布直方图；

(3)、第十六届“华罗庚数学奖”得主徐宗本院士获奖时的年龄为68岁，他的获奖年龄比一半以上“华罗庚数学奖”得主获奖年龄（填“小”或“大”），理由是．

查看试题解析

29. 已知：如图， $A$ ， $B$ 是直线 $l$ 上两点， $A B ∥ C D$ ，连接 $A D$ ， $B D$ ， $B C$ ，若 $B D$ 平分 $∠ A B C$ ， $∠ 1 + ∠ 2 = 180 °$ ．

(1)、请你猜想 $A D$ 与 $B C$ 的位置关系，并证明；

(2)、若 $∠ D A B = α$ ，求 $∠ C D B$ 的大小（用含 $α$ 的式子表示）．

查看试题解析
30. 对于平面直角坐标系 $x O y$ 中的图形 $M$ 和图形 $M$ 上的任意点 $P (x ， y)$ ，给出如下定义：将点 $P (x ， y)$ 平移到 $P^{'} (x + t ， y - t)$ 称为将点 $P$ 进行“ $t$ 型平移”，点 $P^{'}$ 称为将点 $P$ 进行“ $t$ 型平移”的对应点；将图形 $M$ 上的所有点进行“ $t$ 型平移”称为将图形 $M$ 进行“ $t$ 型平移”．例如，将点 $P (x ， y)$ 平移到 $P^{'} (x + 1 ， y - 1)$ 称为将点 $P$ 进行“1型平移”，将点 $P (x ， y)$ 平移到 $P^{'} (x - 1 ， y + 1)$ 称为将点 $P$ 进行“ $- 1$ 型平移”．已知点 $A (2 ， 3)$ 和点 $B (4 ， 3)$ ．

(1)、①将点 $A (2 ， 3)$ 进行“1型平移”后的对应点 $A^{'}$ 的坐标为；②将线段 $A B$ 进行“ $- 1$ 型平移”后得到线段 $A^{'} B^{'}$ ，点 $P_{1} (1 ， 2)$ ， $P_{2} (0 ， 4)$ ， $P_{3} (3 ， 4)$ 中，在线段 $A^{'} B^{'}$ 上的点是．

(2)、若线段 $A B$ 进行“ $t$ 型平移”后与坐标轴有公共点，则 $t$ 的取值范围是．

(3)、已知点 $C (3 ， 0)$ ， $D (5 ， - 2)$ ，点 $E$ 是线段 $C D$ 上的一个动点，将点 $B$ 进行“ $t$ 型平移”后得到的对应点为 $B^{'}$ ，若 $B^{^{'}} E$ 的最小值保持不变，直接写出 $t$ 的取值范围．

查看试题解析