北京市西城区2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 实数3.1415， $\sqrt[3]{2}$ ， $- \frac{5}{7}$ ， $\sqrt{9}$ 中，无理数是（）

A、3.1415 B、 $\sqrt[3]{2}$ C、 $- \frac{5}{7}$ D、 $\sqrt{9}$

查看试题解析
2. 若 $m < n$ ，则下列各式中正确的是（）

A、 $m - n > 0$ B、 $m - 9 > n - 9$ C、 $m + n < 2 n$ D、 $- \frac{m}{4} < - \frac{n}{4}$

查看试题解析
3. 如图，直线 $A B ， C D$ 相交于点O， $E O ⊥ A B$ ，垂足为O， $∠ D O E = 37 °$ ， $∠ C O B$ 的大小是（）

A、 $53 °$ B、 $143 °$ C、 $117 °$ D、 $127 °$

查看试题解析
4. 下列命题中，是假命题的是（）

A、如果两个角相等，那么它们是对顶角 B、同旁内角互补，两直线平行 C、如果 $a = b$ ， $b = c$ ，那么 $a = c$ D、负数没有平方根

查看试题解析
5. 在平面直角坐标系中，点 $A (1 ， 5)$ ， $B (m - 2 ， m + 1)$ ，若直线 $A B$ 与y轴垂直，则m的值为（）

A、0 B、3 C、4 D、7

查看试题解析
6. 以下抽样调查中，选取的样本具有代表性的是（）

A、了解某公园的平均日客流量，选择在周末进行调查 B、了解某校七年级学生的身高，对该校七年级某班男生进行调查 C、了解某小区居民坚持进行垃圾分类的情况，对小区活动中心的老年人进行调查 D、了解某校学生每天体育锻炼的时长，从该校所有班级中各随机选取5人进行调查

查看试题解析
7. 以某公园西门O为原点建立平面直角坐标系，东门A和景点B的坐标分别是 $(6 ， 0)$ 和 $(4 ， 4)$ ．如图1，甲的游览路线是： $O \to B \to A$ ，其折线段的路程总长记为 $l_{1}$ ．如图2，景点C和D分别在线段 $O B ， B A$ 上，乙的游览路线是： $O \to C \to D \to A$ ，其折线段的路程总长记为 $l_{2}$ ．如图3，景点E和G分别在线段 $O B ， B A$ 上，景点F在线段 $O A$ 上，丙的游览路线是： $O \to E \to F \to G \to A$ ，其折线段的路程总长记为 $l_{3}$ ．下列 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 的大小关系正确的是（）

A、 $l_{1} = l_{2} = l_{3}$ B、 $l_{1} < l_{2}$ 且 $l_{2} = l_{3}$ C、 $l_{2} < l_{1} < l_{3}$ D、 $l_{1} > l_{2}$ 且 $l_{1} = l_{3}$

查看试题解析
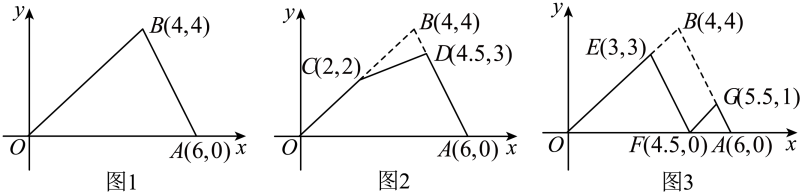8. 有8张形状、大小完全相同的小长方形卡片，将它们按如图所示的方式（不重叠）放置在大长方形 $A B C D$ 中，根据图中标出的数据，1张小长方形卡片的面积是（）

A、72 B、68 C、64 D、60

查看试题解析

二、填空题

9. 若 ${\begin{array}{l} x = 3 ， \\ y = - 2 \end{array}$ 是方程 $a x + y = 10$ 的解，则a的值为．

查看试题解析
10. 在平面直角坐标系中，已知点P在第四象限，且点P到两坐标轴的距离相等，写出一个符合条件的点P的坐标：．

查看试题解析
11. 若一个数的平方等于 $\frac{9}{64}$ ，则这个数是．

查看试题解析
12. 如图，在三角形 $A B C$ 中， $∠ C = 90 °$ ，点 $B$ 到直线 $A C$ 的距离是线段的长， $B C < B A$ 的依据是．

查看试题解析
13. 点M，N，P，Q在数轴上的位置如图所示，这四个点中有一个点表示实数 $\sqrt{5} - 1$ ，这个点是．

查看试题解析
14. 解方程组 ${\begin{array}{l} 3 x + 4 y = 16 ， ① \\ 5 x - 6 y = 33 ， ② \end{array}$ 小红的思路是：用① $\times 5 -$ ② $\times 3$ 消去未知数 $x$ ，请你写出一种用加减消元法消去未知数 $y$ 的思路：用消去未知数 $y$ ．

查看试题解析
15. 如图，四边形纸片 $A B C D$ ， $A D ∥ B C$ ．折叠纸片 $A B C D$ ，使点D落在 $A B$ 上的点 $D_{1}$ 处，点C落在点 $C_{1}$ 处，折痕为 $E F$ ．若 $∠ E F C = 102 °$ ，则 $∠ A E D_{1} =$ $°$ ．

查看试题解析
16. 小明沿街心公园的环形跑道从起点出发按逆时针方向跑步，他用软件记录了跑步的轨迹，他每跑 $1 k m$ 软件会在运动轨迹上标注相应的路程，前 $5 k m$ 的记录如图所示．已知该环形跑道一圈的周长大于 $1 k m$ ．

(1)、小明恰好跑3圈时，路程是否超过了 $5 k m$ ？答：（填“是”或“否”）；

(2)、小明共跑了 $14 k m$ 且恰好回到起点，那么他共跑了圈．

查看试题解析

三、解答题

17. 计算： $3 \sqrt{3} + \sqrt{4} + | - \sqrt{3} | + \sqrt[3]{- 8}$ ．

查看试题解析
18.

(1)、解方程组 ${\begin{array}{l} 2 x + y = 0 ， \\ 2 x + 3 y = 8 . \end{array}$

(2)、解不等式组 ${\begin{array}{l} 4 x + 1 \leq 2 x + 7 ， \\ \frac{2 x + 8}{3} > 1 - x ， \end{array}$ 并写出它的所有整数解．

查看试题解析
19. 如图，点E，F分别在 $B A ， D C$ 的延长线上，直线 $E F$ 分别交 $A D ， B C$ 于点G，H， $∠ B = ∠ D$ ， $∠ E = ∠ F$ ．
求证： $∠ E G A + ∠ C H G = 180 °$
请将下面的证明过程补充完整：

证明：∵ $∠ E = ∠ F$ ，
∴       ▲   $∥$        ▲  ．
∴ $∠ D = ∠$        ▲  ．（    ）（填推理的依据）
∵ $∠ B = ∠ D$ ，
∴ $∠ B = ∠$        ▲  ．
∴       ▲   $∥$        ▲  ．（    ）（填推理的依据）
∴ $∠ D G H + ∠ C H G = 180 °$ ．
∵ $∠ D G H = ∠ E G A$ ，（    ）（填推理的依据）
∴ $∠ E G A + ∠ C H G = 180 °$ ．

查看试题解析
20. 为鼓励同学们参加主题为“阅读润泽心灵，文字见证成长”的读书月活动，学校计划购进一批科技类和文学类图书作为活动奖品．已知同类图书中每本书价格相同，购买2本科技类图书和3本文学类图书需131元，购买4本科技类图书和5本文学类图书需237元．

(1)、科技类图书和文学类图书每本各多少元？

(2)、经过评选有300名同学在活动中获奖，学校对每位获奖同学奖励一本科技类或文学类图书．如果学校用于购买奖品的资金不超过8000元，那么科技类图书最多能买多少本？

查看试题解析
21. 如图，在平面直角坐标系 $x O y$ 中，三角形 $A B C$ 三个顶点的坐标分别是 $A (3 ， 4)$ ， $B (2 ， 1)$ ， $C (5 ， - 1)$ ．将三角形 $A B C$ 先向左平移5个单位长度，再向下平移4个单位长度后得到三角形 $D E F$ ，其中点D，E，F分别为点A，B，C的对应点．

(1)、在图中画出三角形 $D E F$ ；

(2)、求三角形 $A B C$ 的面积；

(3)、若三角形 $A B C$ 内一点P经过上述平移后的对应点为 $Q (m ， n)$ ，直接写出点P的坐标（用含m，n的式子表示）．

查看试题解析
22. 《北京市节水条例》自 $2023$ 年3月1日起实施．学校组织了“珍惜水资源，节水从我做起”的活动，号召大家节约用水．为了解所居住小区家庭用水的情况，小芸从该小区的住户中随机抽取了部分家庭，获得了这些家庭4月份用水量（单位：t）的数据，并对这些数据进行整理和描述．数据分成5组： $0 \leq x < 4$ ， $4 \leq x < 8$ ， $8 \leq x < 12$ ， $12 \leq x < 16$ ， $16 \leq x < 20$ ．下面给出了部分信息：
a.4月份用水量的数据的扇形图、频数分布直方图分别如图1，图2所示．

b.4月份用水量的数据在 $12 \leq x < 16$ 这一组的是： $12$ $12.5$ $12.5$ $13$ $13$ $14$ $15.5$ $15.5$
根据以上信息，回答下列问题：

(1)、小芸共抽取了户家庭进行调查；

(2)、扇形图中， $8 \leq x < 12$ 这一组所对应的扇形的圆心角的度数为°， $n % =$ %；

(3)、补全频数分布直方图；

(4)、请你根据小芸的调查结果，估计该小区480户家庭中有多少户家庭年用水量超过180t．

查看试题解析
23. 将三角形 $A B C$ 和三角形 $D E F$ 按图1所示的方式摆放，其中 $∠ A C B = ∠ D F E = 90 °$ ， $∠ D E F = ∠ E D F = 45 °$ ， $∠ A B C = 30 °$ ， $∠ B A C = 60 °$ ，点D，A，F，B在同一条直线上．

(1)、将图1中的三角形 $A B C$ 绕点B及逆时针旋转，且点A在直线 $D F$ 的下方．
①如图2，当 $A C ∥ D F$ 时，求证： $E F ∥ B C$ ；
②当 $A C ∥ D E$ 时，直接写出 $∠ F B A$ 的度数；

(2)、将图1中的三角形 $D E F$ 绕点E逆时针旋转，如图3，当点D首次落在边 $B C$ 上时，过点E作 $E G ∥ B C$ ，作射线 $D M$ 平分 $∠ F D B$ ，作射线 $E N$ 平分 $∠ G E D$ 交 $D M$ 的反向延长线于点N，依题意补全图形并求 $∠ E N D$ 的度数．

查看试题解析
24. 在平面直角坐标系 $x O y$ 中，已知点 $M (a ， b)$ ，对于点 $P (x ， y)$ ，将点 $Q (x + a ， y - b)$ 称为点 $P$ 关于点 $M$ 的关联点．

(1)、点 $P (- 6 ， 7)$ 关于点 $M (2 ， 3)$ 的关联点 $Q$ 的坐标是；

(2)、点 $A (1 ， - 1)$ ， $B (5 ， - 1)$ ，以 $A B$ 为边在直线 $A B$ 的下方作正方形 $A B C D$ ．点 $E (- 4 ， 1)$ ， $F (- 2 ， 2)$ ， $G (- 1 ， 0)$ 关于点 $M (a ， 4)$ 的关联点分别是点 $E_{1}$ ， $F_{1}$ ， $G_{1}$ ．若三角形 $E_{1} F_{1} G_{1}$ 与正方形 $A B C D$ 有公共点，直接写出 $a$ 的取值范围；

(3)、点 $P (- 1 ， t - 1)$ ， $N (2 t ， 5 t)$ 关于点 $M (3 ， b)$ 的关联点分别是点 $P_{1}$ ， $N_{1}$ ，且点 $P_{1}$ 在 $x$ 轴上，点 $O$ 为原点，三角形 $O P_{1} N_{1}$ 的面积为 $3$ ，求点 $N_{1}$ 的坐标．

查看试题解析
25. 在边长为1的正方形网格中，网格线交点称为格点，顶点都在格点上的多边形称为格点多边形．将格点多边形边上（含顶点）的格点个数记为M，内部的格点个数记为N，其面积记为S，它们满足公式 $S = a M + N + b$ ．小东忘记了公式中a，b的值，他想到可以借助两个特殊格点多边形求出a，b的值．小东画出一个格点四边形 $A B C D$ （如图1），它所对应的 $M = 6$ ， $N = 1$ ， $S = 3$ ．

(1)、请在图2中画出一个格点三角形 $E F G$ ，并直接写出它所对应的M，N，S的值；

(2)、求a，b的值．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，已知点 $P (x_{1} ， y_{1})$ ， $Q (x_{2} ， y_{2})$ ，给出如下定义： $M [P ， Q] = \frac{1}{2} (x_{1} + x_{2} - | x_{1} - x_{2} |) + \frac{1}{2} (y_{1} + y_{2} - | y_{1} - y_{2} |)$ ．

(1)、已知点 $P (1 ， 0)$ ．
①若点Q与点P重合，则 $M [P ， Q] =$ ；
②若点 $Q (3 ， - 1)$ ，则 $M [P ， Q] =$ ；

(2)、正方形四个顶点的坐标分别是 $O (0 ， 0)$ ， $A (t ， 0)$ ， $B (t ， t)$ ， $C (0 ， t)$ ，其中 $t > 0$ ，在正方形 $O A B C$ 内部有一点 $P (a ， b)$ ，动点Q在正方形 $O A B C$ 的边上及其内部运动．若 $M [P ， Q] = a + b$ ，求所有满足条件的点Q组成的图形的面积（用含a，b，t的式子表示）；

(3)、若点 $P (1 ， 2)$ ， $Q (k ， 5 - k)$ ， $M [P ， Q] > 0$ ，且 $M [P ， Q]$ 为奇数，直接写出k的取值范围．

查看试题解析