河北省石家庄市高邑县2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-07-26 类型:期末考试
一、单选题
-
1. 的值是( )A、 B、3 C、 D、2. 不等式的解集在数轴上表示为( )A、
 B、
B、 C、
C、 D、
D、 3. 把 写成 ( , 为整数)的形式,则 为( )A、 B、 C、 D、4. 下列各式的计算结果为a7的是( )A、(﹣a)2•(﹣a)5 B、(﹣a)2•(﹣a5) C、(﹣a2)•(﹣a)5 D、(﹣a)•(﹣a)65. 等腰三角形的周长为15,其一边长为3,则另两边的长分别为( )A、9,3 B、6,6 C、9,3或6,6 D、6,36. 下列各式从左到右变形是因式分解,并分解正确的是( )A、 B、 C、 D、7. 如图,若 , 则下列结论正确的是( )
3. 把 写成 ( , 为整数)的形式,则 为( )A、 B、 C、 D、4. 下列各式的计算结果为a7的是( )A、(﹣a)2•(﹣a)5 B、(﹣a)2•(﹣a5) C、(﹣a2)•(﹣a)5 D、(﹣a)•(﹣a)65. 等腰三角形的周长为15,其一边长为3,则另两边的长分别为( )A、9,3 B、6,6 C、9,3或6,6 D、6,36. 下列各式从左到右变形是因式分解,并分解正确的是( )A、 B、 C、 D、7. 如图,若 , 则下列结论正确的是( )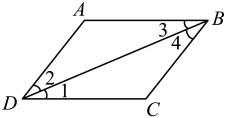 A、∠1=∠2 B、∠2=∠3 C、∠1=∠3 D、∠2=∠48. 如图,边长为、的长方形周长为 , 面积为 , 则的值为( )
A、∠1=∠2 B、∠2=∠3 C、∠1=∠3 D、∠2=∠48. 如图,边长为、的长方形周长为 , 面积为 , 则的值为( )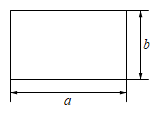 A、 B、 C、 D、9. 下列说法正确的是( )
A、 B、 C、 D、9. 下列说法正确的是( )①等腰三角形是等边三角形;
②三角形按边可分为等腰三角形、等边三角形和不等边三角形;
③等腰三角形至少有两边相等;
④三角形按角分为锐角三角形、直角三角形和钝角三角形.
A、①② B、③④ C、①②③④ D、①②④10. 用加减法解方程组时,最简捷的方法是( )A、①×4-②×3,消去x B、①×4+②×3,消去x C、②×2+1,消去y D、②×2-①,消去y11. 若 , 则n的值是( )A、2023 B、2022 C、2021 D、202012. 如图,正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼成一个长为(),宽为()的大长方形,那么需要C类卡片张数为( ) A、4 B、5 C、6 D、713. 关于的不等式组有三个整数解,则的取值范围( )A、 B、 C、 D、14. 如图,点 , 分别在直线 , 上,点 , 在两直线之间,线段与相交于点 , 且有 , . 三人说法如下:甲:;乙:;丙: . 下列判断正确的是( )
A、4 B、5 C、6 D、713. 关于的不等式组有三个整数解,则的取值范围( )A、 B、 C、 D、14. 如图,点 , 分别在直线 , 上,点 , 在两直线之间,线段与相交于点 , 且有 , . 三人说法如下:甲:;乙:;丙: . 下列判断正确的是( ) A、甲错,乙对 B、甲对,乙错 C、甲对,丙对 D、乙对,丙错15. 如图,七个相同的小长方形组成一个大长方形 , 若 , 则长方形的周长为( )
A、甲错,乙对 B、甲对,乙错 C、甲对,丙对 D、乙对,丙错15. 如图,七个相同的小长方形组成一个大长方形 , 若 , 则长方形的周长为( )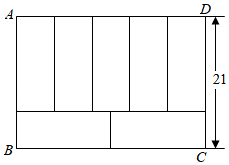 A、100 B、102 C、104 D、10616. 对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“判断结果是否大于190?”为一次操作,如果操作恰好进行两次就停止了,那么x的取值范围是( )
A、100 B、102 C、104 D、10616. 对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“判断结果是否大于190?”为一次操作,如果操作恰好进行两次就停止了,那么x的取值范围是( ) A、8<x≤22 B、8≤x<22 C、8<x≤64 D、22<x≤64
A、8<x≤22 B、8≤x<22 C、8<x≤64 D、22<x≤64二、填空题
-
17. 若7﹣2×7﹣1×70=7p , 则p的值为 .18. 一种苹果的进价是每千克1.9元,销售中估计有5%的苹果正常损耗,商家把售价至少定为元,才能避免亏本.19. 如图是可调躺椅示意图(数据如图),AE与BD的交点为C,且∠A,∠B,∠E保持不变.为了舒适,需调整∠D的大小,使 , 则图中∠D应(填“增加”或“减少”)度.

三、解答题
-
20. 已知是方程2x-ay=9的一个解,解决下列问题:(1)、求的值;(2)、化简并求值:21.(1)、因式分解: .(2)、解不等式组22. 如图,∠AFD=∠1,AC∥DE .
 (1)、试说明:DF∥BC;(2)、若∠1=70°,DF平分∠ADE , 求∠B的度数.23. 有甲、乙两个长方形纸片,边长如图所示(m>0),面积分别为S甲和S乙 .
(1)、试说明:DF∥BC;(2)、若∠1=70°,DF平分∠ADE , 求∠B的度数.23. 有甲、乙两个长方形纸片,边长如图所示(m>0),面积分别为S甲和S乙 . (1)、①计算:S甲= , S乙=;
(1)、①计算:S甲= , S乙=;②用“<”,“=”或“>”填空:S甲 S乙 .
(2)、若一个正方形纸片的周长与乙长方形的周长相等,面积为S正 .①该正方形的边长是 ▲ (用含m的代数式表示);
②小方同学发现:S正与S乙的差与m无关.请判断小方的发现是否正确,并通过计算说明你的理由.
24. 分解因式x2-4y2-2x+4y,细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式,过程为:x2-4y2-2x+4y=(x+2y)(x-2y)-2(x-2y)=(x-2y)(x+2y-2).这种分解因式的方法叫分组分解法,利用这种方法解决下列问题:(1)、分解因式:a2-4a-b2+4;(2)、若△ABC三边a、b、c满足a2-ab-ac+bc=0,试判断△ABC的形状.25. 某学校期末需要表彰优秀学生,计划购买一部分笔记本和证书,已知购买50个笔记本和60张证书需要324元,购买40个笔记本和200张证书需要320元.(1)、求一个笔记本和一个证书的价钱;(2)、某文具用品商店给出两种优惠方案:甲:买一个笔记本,赠送一张证书;
乙:购买200张证书以上,超过200张的证书按原价的打八折,笔记本不打折.
学校准备购买80本笔记本,证书若干张(超过200张),请你判断哪种方案更合算,并说明理由.
26. 如图,已知AM∥BN,∠A=52°,点P是射线AM上的动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.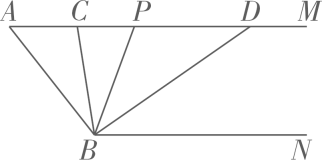 (1)、求∠CBD的度数;(2)、当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由,若变化,请写出变化规律;(3)、当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
(1)、求∠CBD的度数;(2)、当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由,若变化,请写出变化规律;(3)、当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.